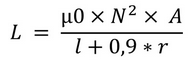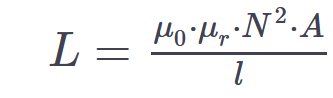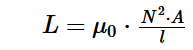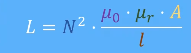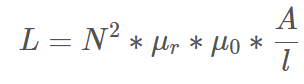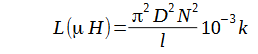|
http://sites.schaltungen.at/elektronik/formeln/induktivitaet
Wels, am 2022-01-12BITTE nützen Sie doch rechts OBEN das Suchfeld [ ] [ Diese Site durchsuchen]DIN A3 oder DIN A4 quer ausdrucken
*******************************************************************************I** DIN A4 ausdrucken (Heftrand 15mm / 5mm) siehe http://sites.schaltungen.at/drucker/sites-prenninger
********************************************************I* ~015_b_PrennIng-a_elektronik-formeln-induktivitaet (xx Seiten)_1a.pdf
Berechnung der Induktivität einer zylindrischen Luftspule
Quelle:
http://sites.schaltungen.at/elektronik/dvb-t-antennen/dipol-antenne
VIDEOs
Induktionsgesetz
VIDEO
https://studyflix.de/elektrotechnik/induktionsgesetz-1896
Elektromagnetische Induktion und Induktionsspule
VIDEO
https://studyflix.de/elektrotechnik/spule-und-induktion-267
Transformator
VIDEO
https://studyflix.de/elektrotechnik/transformator-1822
Grundbegriffe der Elektrotechnik
VIDEO
https://studyflix.de/elektrotechnik/thema/elektrotechnik-grundlagen-20
Schwingkreis
VIDEO
https://studyflix.de/elektrotechnik/schwingkreis-1540
VIDEO
https://studyflix.de/elektrotechnik/selbstinduktion-1777
********************************************************I*
Induktivität einer Spule berechnen Induktivität mit Schalenkern, Berechnung von L, Al, und N, Induktivität mit Ringkern, Berechnung der Induktivität L, des Al-Wertes und der Windungszahl N
Induktivität und Windungszahl für mehrlagige Zylinderspulen (Luftspulen)
Induktivität einer quadratischen Printspule Induktivität einer runden Printspule Speicherdrosseln für Schaltnetzteile (SNT)
Umrechnung der Drahtwerte AWG, mm und qmm
Tabelle über Ferritkerne mit Luftspalt, z. B. für Speicherdrosseln in SNT Tabelle über Kupferlackdraht, CuL Tabelle über Transformatoren mit EI-Schnitt
EPCOS / TDK Website, Ferrite und Zubehör Technische Informationen zu Induktivitäten mit F
Quelle: https://www.electronicdeveloper.de/LL_Induktivitaet.aspx
Ein-Ausschaltvorgang einer Spule
https://www.physikalische-schulexperimente.de/physo/Ein-Ausschaltvorgang_einer_Spule
********************************************************I*
Zylindrische Luftspulen bauen & berechnen
Als Wickelkörper eignen sich ganz gut Elektro-Installationsrohe aus dem Baumarkt.
Formeln zur Berechnung Für die Berechnung von Luftspulen reichen in der Praxis meist einfache Näherungsformeln aus.
Diese findet man in diversen Fachbüchern und auf Wikipeadia.
Grundsätzlich muss unterschieden werden, ob man kurze oder lange Luftspulen bauen will.
Bei kürzeren Spulen nimmt die magnetische Kopplung zwischen den einzelnen Windungen zu.
Längen werden in Millimeter angeben, Induktivitäten in Millihenry.
L= Induktivität in mH
D = mittlerer Spulendurchmesser in mm
l = Länge in mm
r = Radius in mm = D / 2
N = Anzahl der Windungen
A = r * r * pi
µ0 = 4*pi * 10^-7 = 1,2566 x 10 hoch -6 = 0,0000012566 = Magnetische Feldkonstante
Möchte man die Induktivität einer kurzen Spule berechnen, so wird neben der magnetischen Feldkonstante (µ0) noch die Spulenlänge (l), die Querschnittsfläche (A) und die Anzahl der Windungen (N) benötigt.
Die Querschnittsfläche (A) setzt sich aus pi*r² zusammen (r = radius).
Nachdem die Längeneinheiten in Millimeter angegeben wurden, wird auch das Ergebnis in der Einheit Millihenry angegeben.
Eine Luftspule gilt als lang, wenn die Spulenlänge größer als der Durchmesser ist. (l = 1,5 bis 5x D)
Die Formel für die Berechnung von langen Spulen ähnelnd der Formel für kurze Spulen.
In der Praxis hat sich jedoch erwiesen, dass die Formel für kurze Luftspulen auch bis zu einer Länge vom doppelten Durchmesser brauchbar ist.
Oft kennt man die benötigte Induktivität bereits oder hat diese errechnet und möchte sich jetzt die dazu passende Luftspule wickeln.
In der Praxis hat sich erwiesen, dass man dies mit einer wilden Wicklung bauen kann, wenn man hierfür eine bestimmte Länge vordefiniert. Die Formelumstellung zur Berechnung der Windungszahl sieht wie folgt aus:
Windungszahl berechnen
Quelle:
https://www.aeq-web.com/luftspulen-selber-bauen-und-berechnen-hochfrequenz-inductor/
********************************************************I*
Induktivität einer SpuleDie Spule speichert magnetische Energie.Die wichtigste Kenngröße der Spule ist die Induktivität. Die Induktivität ist ein Maß für die Speicherfähigkeit von magnetischer Energie. Die Induktivität wird als Verhältnis des gesamten magnetischen Flusses NΦ zur Stromstärke I definiert: L = N⋅Φ/I Einheit [L] = Vs/A = H (Henry) Formel für die Berechnung einer Induktvität L = µ0⋅ µr⋅ A⋅ N² / lm L = N² x (µ0*µr*A/l)
D = innen Durchmesser
L = Induktivität N = Anzahl der Windungen µ0 = Magnetische Feldkonstante = 4pi * 10^-7 = 1,2566 x 10 hoch -6 = 0,0000012566 µ0: magnetische Feldkonstante µ0 = 1,2566⋅10-6 Vs/Am. µr = Permiabilität von Luft 1 + 0,4*10^-6 Permeabilitätszahl 1,0000004 Ohm
µr = Materialkonstante
A: Querschnitt des Spulenkerns
A = Querschnittsfläche der Spule = d2*pi/4 = r2*pi (von einer Windung eingeschlossene Fläche (meistens kreisförmig))
Querschnittsfläche senkrecht zur Spulenachse.
N: Windungszahl
lm: mittlere Feldlinienlänge im Eisenkern l = Länge der Spule Lange Spule l = 1 bis 5x Durchmesser
1e^-2 = 0.01
Spule Der magnetische Fluss Φ kann anschaulich als die "Anzahl" dermagnetischen Feldlinien gedeutet werden
Quelle:
http://home.teleos-web.de/vsteinkamp/get/spule/spule.htm
********************************************************I*
Induktivitätsberechnung einer Zylinderspule
z.B.
N = 6000 Wdg. (Drahtwindungen)
l = 15cm = 0,15m (Spulenlänge)
D = 5,046 cm (Spulendurchmesser)
A = D^2 * pi / 4 = 20cm2 = 20 *10^-4 = 0,002m2
µ0 = Magnetische Feldkonstante = 4pi * 10^-7 = 1,2566 x 10 hoch -6 = 0,0000012566
L = 0,0000012566 * 6000^2 * 0,002 / 0,15 = 602,88 mH
Quelle:
https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-induktion/aufgabe/induktivitaetsberechnung
https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-induktion/grundwissen/selbstinduktion-und-induktivitaet
https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-induktion/aufgabe/rund-um-die-selbstinduktion
https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-induktion/aufgabe/magnetische-energie
https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-induktion/aufgabe/ziehen-eines-eisenkerns-aus-einer-spule
https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-induktion/aufgabe/induktion-beim-lautsprecher-abitur-bw-1996-lk
********************************************************I*
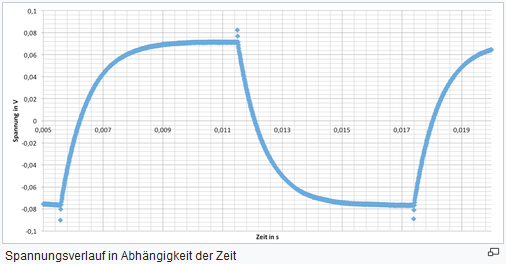
Die Spule im Gleichstromkreis
Quelle:
https://www.elektroniktutor.de/analogtechnik/l_gleich.html
Ein-Ausschaltvorgang einer Spule
Quelle:
https://www.physikalische-schulexperimente.de/physo/Ein-Ausschaltvorgang_einer_Spule
********************************************************I*
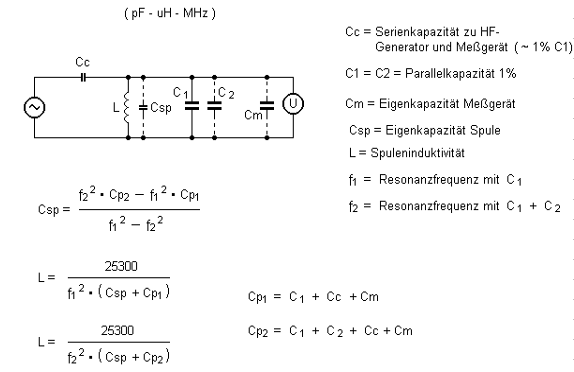
Eigenkapazität und Induktivität einer Spule
L = N² x (µ0*µr*A/l)
L = µ0*µr*(A*N² / l)
D = innen Durchmesser
L = Induktivität in Henry
N = Anzahl der Windungen
µ0 = Magnetische Feldkonstante = 4pi * 10^-7 = 1,2566 x 10 hoch -6 = 0,0000012566 (N/A²)
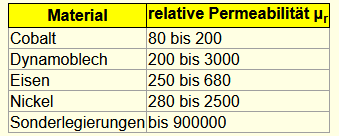
µr = relative Permeabilität von Luft 1 + 0,4*10^-6 Permeabilitätszahl 1,0000004 Ohm
µr = relative Permeabilität mit Eisenkern Permeabilitätszahl 300 .. 10.000 Ohm
l = Länge der Spule in m
A = Querschnittsfläche der Spule in m2 = d2*pi/4 = r2*pi (von einer Windung eingeschlossene Fläche (meistens kreisförmig))
Querschnittsfläche senkrecht zur Spulenachse.
Lange Spule l = 1 bis 5x Durchmesser
Dm = mittlerer Durchmesser
L = µ*N²*A/l
µ = µ0*µr L ... Induktivität µr ... Permeabilität von Luft 1 + 4*10-7 N ... Windungszahl (N² ist das Quadrat davon) A ... die Fläche der Spule (Radius zum Quadrat mal pi = 3,14 A = R² * pi) l ... Länge der Spule A ist die durchflutete Querschnittsfläche, einer Leiterschleife A=pi/4*d*d A = pi*r*r
noch ein kleiner Tipp:
die Spulen gut verkleben damit sie nicht vibrieren können.
Ausreichend dicken Draht (0,7..1mm) nehmen damit möglichst wenig Kupferverluste entstehen.
d = Drahtdurchmesser 1mm
N = 20 Wdg.
N² = 400
µr = 1 + 0,0000004 = 1,0000004
µ0 = Magnetische Feldkonstante = 4pi * 10^-7 = 1,2566 x 10 hoch -6 = 0,0000012566 (N/A²)
µ = µr * µ0 = 1,0000004 * 0,0000012566 =
Dm = 21mm
A = D2 + pi/4 = 21² * 3,14 / 4 = 346,3mm2 = 346,3*10-6m2
Länge einer Windung = D * 3,14 = 21 * 3,14 = 65,97mm
Länge einer 20 Wdg = 21 * 3,14 * 20 = 1319mm
l = Länge der Spule = 20 x 1mm = 20mm
L = µ*N²*A/l = 1,0 * 400 * 0,000346m2 / 0,020m = 6,92uH
Induktivität und Spule
Induktivität einer Toroid- oder Ringspule / Ringkernspule
N = Anzahl der Windungen
u0 = Magnetische feldkonstante
ur = Permiabilität
l = länge der spule
A = Querschnittsfläche der Spule
R = Äußerer Radius
r = Innerer Radius
h = Höhe des Spulenkernes
oder
D = Breite des Spulenkernes
z.B.
R = 40mm
r = 32mm
r = (40-32) / 4 =
Quelle:
https://studyflix.de/elektrotechnik/induktivitat-und-spule-1542
https://www.elektroniktutor.de/bauteilkunde/spule.html
********************************************************I*
Induktivität einer Luftspule bzw. Rahmenantenne
 In der Hochfrequenztechnik und somit im Amateurfunk werden an verschiedenen Stellen Induktivitäten eingesetzt.
Insbesondere bei Anpassnetzwerken, Filtern und Schwingkreisen.
Auch im Antennenbau sind Induktivitäten ein wichtiges passives Bauelement.
Die Maßeinheit für die Induktivität ist das Henry (H) und wurde nach dem amerikanischen Physiker Joseph Henry benannt.
Das Henry lässt sich auch aus den SI-Basiseinheiten entwickeln und hat dann die Einheit Vs/A.
Warum das hier erläutert wird, sehen Sie gleich, wenn eine Luftspule berechnet wird.
Berechnung der Induktivität einer Luftspule. Anlass dieser Betrachtung ist der Wunsch, eine Rahmenantenne zum Empfang des Maschinensenders SAQ in Grimeton (Schweden) zu bauen.
Die Rahmenantenne ist vom Grundsatz her nichts anderes als eine Luftspule.
Die Berechnung sollte daher mit einschlägigen Formeln möglich sein.
Eine Formel, die sicherlich auch dem interessierten Laien bekannt sein könnte, beschreibt die Induktivität einer Luftspule wie folgt:
Lange Spule
µ0 = magnetische Feldkonstante = 4pi * 10^-7 = 1,2566 x 10^-6 = 0,0000012566 (N/A²)
A = Querschnittsfläche der Spule l = Länge der Spule Diese Formel funktioniert allerdings nur, wenn die Länge der Spule 2x größer als ihr Durchmesser ist.
Betrachtet mal Luftspulen , die als Bauelement in einer Schaltung eingesetzt werden sollen, ist dieses sicherlich so anzunehmen.
Beim Bau einer Rahmenantenne ist dieses Verhältnis aber genau anders herum.
Der Durchmesser der Spule ist deutlich größer als deren Länge.
Wendet man die obige Formel dennoch bei einer solchen Spulenanordnung (Rahmenantenne) an, so erhält man Induktionswerte, die schnell um den Faktor 10 zu groß sein können.
In der Literatur findet man daher eine Formel zur Berechnung einer solchen kurzen Luftspule, die einen Korrekturfaktor einhält.
Länge der Spule ist kleiner als ihr Durchmesser.
Kurze Spule
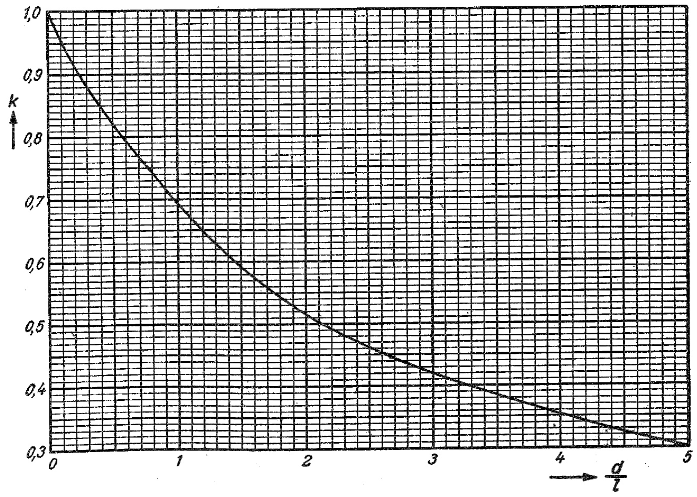
 Wobei k der Korrekturfaktor ist, der nicht näher angegeben wird und experimentell ermittelt werden muss.
OM Schau, DL3LH, gibt in einer Abhandlung über „Induktivitäten in der täglichen Amateurfunkpraxis“ Korrekturwerte für kurze Luftspulen mit einem Verhältnis von d/l bis 10 an.
Bei einer Rahmenantenne für VLF kann dieses Verhältnis aber auch eventuell bei 40 liegen.
Ich habe daher die Werte von DL3LH in eine Exceltabelle eingetragen und versucht grafisch weiterzuentwickeln.
Das nachfolgende Diagramm zeigt das Ergebnis:
Korrekturfaktor einer Luftspule (Formfaktor)
Eine so berechnete Induktivität einer Rahmenantenne entsprach zwar immer noch nicht dem gemessenen Wert, war aber immerhin schon in der gleichen Größenordnung. Eigenkapazität Beim Einsatz von Spulen werden gerne schon mal die Verluste einer Induktivität, allen voran die Eigenkapazität vergessen.
So erging es mir bei der Konstruktion einer Rahmenantenne für VLF.
Die Größe der Eigenkapazität hatte ich deutlich unterschätzt.
Gerade beim Einsatz der Induktivität in einem Schwingkreis spielt die Eigenkapazität eine große Rolle.
Beeinflusst sie doch die Resonanzfrequenz des Kreises.
Die Eigenkapazität kann man sich als eine zur Induktivität parallel geschalteten Kondensator vorstellen.
So stellt eine Rahmenantenne für sich allein schon einen Schwingkreis mit einer Eigenresonanzfrequenz dar.
Diese Frequenz ist zugleich die höchste Frequenz auf die in einem Schwingkreis abgestimmt werden kann.
Die Resonanzfrequenz kann messtechnisch ermittelt werden.
Aber dazu in einem eigenen Beitrag mehr.
Rechnerisch lässt sich die Eigenkapazität kaum bestimmen.
Als Faustformal kann angenommen werden, dass die Eigenkapazität in pF etwa dem Spulendurchmesser in cm entspricht.
Aber auch dies gilt nur für Spulen bei denen ihre Länge größer als ihr Durchmesser ist.
Bei anderen Anordnungen bleibt nur die messtechnische Bestimmung.
Eins ist allerdings zu beobachten.
Die Eigenkapazität ist proportional zum Spulendurchmesser.
Beispiel:
5-facher Durchmesser bewirkt auch 5-fache Eigenkapazität. Der berechnete Wert ist aber für die weiteren Betrachtungen brauchbar und sowieso besser, als wenn man komplett im Dunkeln tappen würde.
Fazit Eine Berechnung einer kurzen Zylinderspule ist mit dem beschriebenen Ansatz nur näherungsweise möglich.
Quelle: http://www.amateurfunk-sauerland.de/technik/induktivitaet-einer-luftspule-bzw-rahmenantenne/
********************************************************I*
Einlagige Luftspule V 1.0
DL1JWD-Spulenrechner 1.0
Programme zur Berechnung von Zylinderspulen gibt es zur Genüge.
Was man aber mit Sicherheit nicht so schnell finden wird ist ein Tool, welches gleichzeitig auch parasitäre Kapazität und Parallelresonanz abschätzt, die optimale Spule vorschlägt und als Zugabe auch noch die geometrischen Abmessungen in natürlicher Größe anzeigt. Exakte Ermittlung der Induktivität Die genaue Berechnung der Induktivität erfordert eine aufwändige Integration über die magnetische Feldverteilung mit Mitteln der Höheren Mathematik, die von meinem Programm verwendeten einfachen Näherungsformeln sind deshalb mehr oder weniger fehlerbehaftet. Zu Vergleichszwecken habe ich auf die aus /1/ entnommene Kurve zurückgegriffen, aus der ein so genannter Formfaktor k als Funktion des Verhältnisses Durchmesser zu Länge abgelesen werden kann:
Korrekturfaktor / Formfaktor k
In meinem Programm habe ich eine approximierende Funktion über obige Kurve gelegt, sodass L für D/l <=5 (l/D > = 0,2) berechnet werden kann und über den Button "Kontrolle" abrufbar ist. Zur Spulengüte Das für die "optimale" Spule gültige Verhältnis l/D = 0,45 muss nicht automatisch auch zu einer Spule mit größtmöglicher Güte führen, bei der ja auch die Drahtstärke (Skineffekt!) eine große Rolle spielt. In /2/ findet der mathematisch interessierte OM dazu eine mutige Veröffentlichung, denn leider üben mathematische Formeln heute auf eine wachsende Mehrheit von Funkamateueren eine eher abschreckende Wirkung aus Literatur /1/ Limann,O.; Hassel,W.: Hilfsbuch für Hochfrequenz-Techniker, Bd.1 , 2.A. Franzis, 1959 /2/ Zwicky, P., HB9DFZ: Optimierung der Güte einlagiger zylindrischer Luftspulen. FUNKAMATEUR 62 (2013) H.10, S. 1080-1084
300_d_fritz-x_Prg. zur Berechnung von einlagige Luftspule V 1.0_1a.pdf
Quelle:
http://dl1jwd.darc.de/Luftspule.pdf
http://dl1jwd.darc.de/sr.html
********************************************************I*
Induktivität einer Luftspule
Normierte Induktivität Lo ( H) einer Luftspule für N = 10 Windungen300_c_fritz-x_Induktivitäten in der täglichen Praxis -Luftspulen (8 Seiten)_1a.pdf
Quelle: http://do8ail.bplaced.net/db0fa/wordpress/wp-content/uploads/2018/05/Induktivitäten-Luftspulen-in-der-tägl.-Praxis.pdf
********************************************************I*
********************************************************I*
DIN A4 ausdrucken
********************************************************I*
Impressum: Fritz Prenninger, Haidestr. 11A, A-4600 Wels, Ober-Österreich, mailto:[email protected]ENDE |
FORMELN >