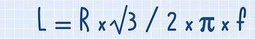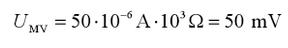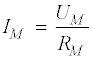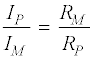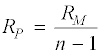|
http://sites.schaltungen.at/elektronik/messen
Wels, am 2016-10-24BITTE nützen Sie doch rechts OBEN das Suchfeld [ ] [ Diese Site durchsuchen]DIN A3 oder DIN A4 quer ausdrucken
*******************************************************************************I** DIN A4 ausdrucken (Heftrand 15mm / 5mm) siehe http://sites.schaltungen.at/drucker/sites-prenninger
********************************************************I* ~015_b_PrennIng-a_elektronik-messen (xx Seiten)_1a.pdf
Untergeordnete Seiten (3):
Vorsicht: Entladung vor der Kapazitätmessung !!
LCR-Meter L-C-R Meter L/C/R Meter
LC-Meter L-C Meter L/C Meter
LCR Tester
LCR-Meter L/Induktivität, C/Kapazität, R/Widerstand
ROHDE&SCHWARZ
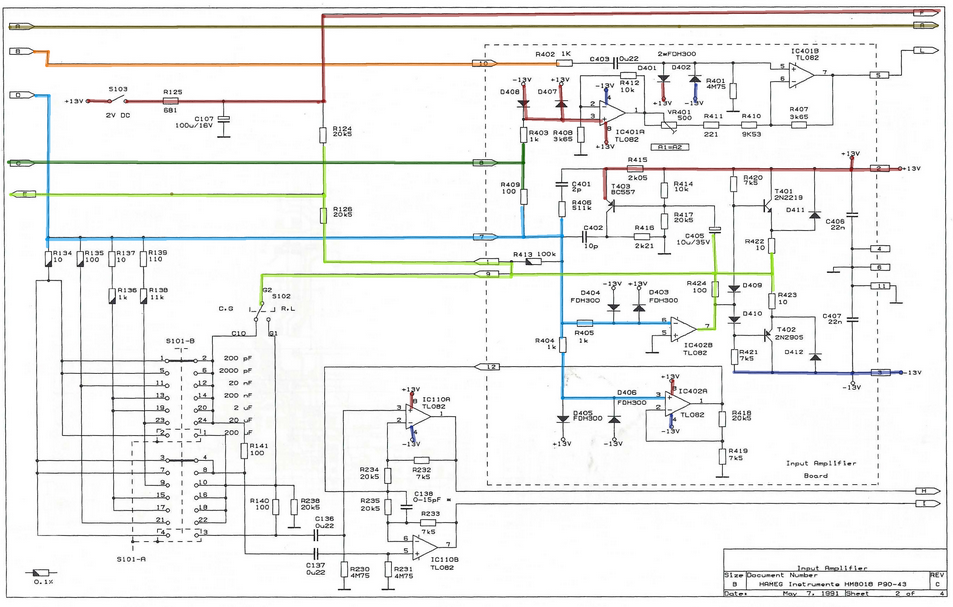
HAMEG HM8018 LC-Meter vorhanden !R&S HM8018 LCR-Meter-Modul 25kHz
Das Rohde & Schwarz HM8018 LCR-Meter Modul ermöglicht Messungen mit 5 Testfrequenzen 100Hz, 120Hz, 1kHz, 10kHz, 25kHz.
Die automatische Messfrequenzwahl ermöglicht die Bauteilemessung immer im praxisgerechten Bereich.
Das Modularsystem HM8000 inkl. seiner Module HM80xx ist abgekündigt seit 31. Dez. 2018.
ALT STAND 1987 DM 528,- ATS 4.400 verkaufe um € 444,-
Mit einer Messrate von 2 Messungen pro Sek. und automatischer Bereichswahl ist komfortables Arbeiten möglich.
Die hohe Genauigkeit des Gerätes erlaubt die Verwendung in allen Bereichen der Elektronik und Elektrotechnik.
Vor allem im Labor- und Service-Betrieb hat sich das LCR-Meter bewährt.
Quelle:
https://www.radiomuseum.org/r/hameg_hm8018hm_801.html
Messfunktionen: L, C, R, Θ, Q, D |Z| Grundgenauigkeit 0,2 % 5 Messfrequenzen: 100 Hz, 120 Hz, 1 kHz, 10 kHz, 25 kHz Maximale Auflösung: 0,001 Ω, 0,001 pF, 0,01 μH 2- und 4-Draht Messung Parallel- und Serienmodus Vorspannung für Elektrolytkondensatoren zuschaltbar Grundgerät HM8001-2 erforderlich Bedienhandbuch
579_d_HAMEG-x_HAMEG HM8018 LCR Meter - L=uH, Rs=k Ohm, C=pF, G=uS (Handbuch)_1a.pdf
579_d_HAMEG-x_HAMEG HM8018 LCR Meter - L=uH, Rs=k Ohm, C=pF, G=uS (Benutzerhandbuch)_1a.pdf
579_d_HAMEG-x_HAMEG HM8018 L-C Meter - L=uH, Rs=k Ohm, C=pF, G=uS (Datenblatt)_1a.pdf
570_d_HAMEG-x_MANUAL HM8018 L-C Meter (Modular-System) Schaltung Print Stückliste_1a.pdf
579_d_HAMEG-x_HAMEG HM8018 L-C Meter - L=uH, Rs=k Ohm, C=pF, G=uS (Techn. Daten)_1a.pdf
579_d_HAMEG-x_HM8018 LCR-Meter - Modular-System (Datenblatt)_1a.pdf
https://www.rohde-schwarz.com/at/produkt/hm8018-produkt-startseite_63493-147341.html
Bedienhandbuch
579_d_HAMEG-x_HAMEG HM8001-2 Mainframe - Grundgerät für 2 Einschübe (Benutzerhandbuch)_1a.pdf
https://scdn.rohde-schwarz.com/ur/pws/dl_downloads/dl_common_library/dl_manuals/gb_1/h/hm800_1/HM800_Blank_Module_UserManual_en_02.pdf
https://allice.de/rohde-schwarz/hm8018-hm8000-serie-lcr-meter-lc-meter-modularsystem-hameg/
https://www.rohde-schwarz.com/at/produkt/hm8018-produkt-startseite_63493-147341.html
********************************************************I*
Eigenbau Kapazitäts- und Induktivitäts-Meßgerät (71) elektor 79636-11
für die Induktivität (Spule)
Quelle:
516_c_1L-4D-4IC-1U-12V_79636-11 Kapazitäts- und Induktivitäts Messgerät § uA747 = TL082 CA3240 4093_1a.pdf
HAMEG HM 8118 LCR-Messbrücke mit 14 verschiedenen Messfunktionen € 2.915,50Das LCR-Meter R&S HM8118 ist mit Messfrequenzen von 20 Hz – 200 kHz zur hochgenauen Messung von Widerständen, Spulen und Kondensatoren ausgestattet.Die (Grund-) Genauigkeit von 0,05 % eine variable Messspannung (0,10…1,50 V rms) sowie eine Bias-DC-Funktion für Spannung (0…5,00 V bzw. 0…40 V ext.) und für Strom (0…200 mA) erlauben die stabile Erfassung selbst sehr kleiner Messwerte • 14 verschiedene Messfunktionen • Messfrequenzbereich von 20 Hz bis 200 kHz • Bis zu 12 Messungen pro Sekunde • Parallel- und Serienmodus • Eingabe von Grenzwerten für automatisches Sortieren von Bauelementen (optional) • Mess- und Biasspannung sowie -Strom intern programmierbar • Messung von Transformatorparametern • Externe Vorspannung von bis zu 40 V zuschaltbar • Galvanisch getrennte USB/RS-232 Schnittstelle, optional: IEEE-488 • Inkl. Kelvin Messkabel (HZ184) und 4-Draht-SMD-Testadapter (HZ188) Rohde & Schwarz HM8118 LC-Meter aus der Value Instruments Serie (vormals Hameg) ist eine sehr gut ausgestattete LCR-Messbrücke mit Messfrequenzen von 20 Hz – 200 kHz, zur hochgenauen Bestimmung von Widerständen, Spulen, Kondensatoren und Transformatoren. Die Messbrücke HM8118 besitzt eine Grund-Genauigkeit von 0,05 % und eignet sich dank ihrer Vielseitigkeit für Entwicklung, Produktion, Service und Ausbildung.
Die Messfrequenz ist von 20 Hz…200 kHz variabel.
Außerdem steht eine variable Messspannung von 0,10V bis 1,50 V sowie eine DC-Bias Funktion für Spannung und Strom zur Verfügung.
Die verwendete Multislope-Wandler-Technologie ermöglicht genaue Messungen bis in den Femto-Farad-Bereich und und den Nano-Henry-Bereich.
Alle Einstellungen und Messungen können über das Frontpanel, aber auch über einen PC erfolgen.
Mit der LCR-Meter HM8118 lassen sich auch die nicht idealen Eigenschaften realer Bauelemente wie den Rs im Serienersatzschaltbild oder den Rp im Parallelersatzschaltbild eines Kondensators oder einer Spule und die sich daraus ableitenden Kenngrößen wie Güte Q, Verlustfaktor D, Phasenwinkel Theta , sowie die komplexen Größen Impedanz Z und Admittanz Y auf Knopfdruck messen.
Alle Parameter der Messung wie Messfrequenz, AC-Messspannung, Bias (U bzw. I), Quellimpedanz (Range), Messgeschwindigkeit (Speed), Status des Leerlauf-, Kurzschluss- und Lastabgleichs werden gleichzeitig mit dem Messergebnis auf dem grafischen LCD zur Anzeige gebracht.
Alle Einstellungen können über das Frontpanel sowie über USB, RS232 oder GPIB erfolgen.
Zum Lieferumfang gehören HZ188 4-Draht-SMD-Testadapter und HZ184 Kelvin Messkabel.
Quelle:
https://allice.de/rohde-schwarz/rohde-schwarz-hm8118-lcr-meter-lc-meter-lcr-messgeraete-hm8000/
LCR-Messgerät
Elektor 2 MHz LCR-Meter Kit € 799.-
Die hohe Genauigkeit dieses Messgeräts und seine erstaunlich einfache Bedienung sind das Ergebnis einer besonders sorgfältigen Entwicklung.
Die Technik hinter der aufgeräumten Frontplatte funktioniert so gut, dass man die verwendeten Messtechniken glatt vergessen kann.
Dies führt zu einer ganz besonderen Gelegenheit für unsere Leser, die sich für hochwertige Messtechnik begeistern.
Wenn Sie wie wir ein Faible für die Wunder moderner Elektronik haben, dann schauen Sie doch einfach mal rein
und sehen sie, wie man damit den Bruchteilen elektronischer Einheiten auf den Zahn fühlen kann.
Elektor 11-12/2020 Seite 38
14. Januar 2016
Quelle:
https://www.elektor.de/elektor-2-mhz-lcr-meter-kit https://www.elektor.de/elektor-11-12-2020-de https://www.elektormagazine.de/news/life-auf-video-lcr-meter-mit-500-ppm-von-elektor ********************************************************I*
LCR Meter 50Hz .. 2 MHz AU2019 v1.2.2 elektor 11/2020 Seite 6
Simple LC Meter Circuit for measuring Inductance and Capacitance at Home
simple L/C meter LC-Meßgerät elektor 07/1980 Seite 44
LC-Meßgerät elektor 07/1984 Seite ??
LC Meter Circuit, Coil Capacitor Meter
Diese LC-Meter-Schaltung kann Spulen und Kondensatoren messen.
Wenn Lx oder Cx in die Schaltung geschaltet wird, sinkt die Oszillatorfrequenz
und diese Abnahme wird durch einen Frequenz-Spannungs-Wandler gemessen, der aus T3 und T4 besteht.
Zum Einstellen dieser lc-Meter-Schaltung mit P1 und P2.
Die Genauigkeit des LC-Messgeräts beträgt 3 %.
Die Skalenkalibrierung kann mit dieser Formel erreicht werden: ni = nm(1 – fr)/(1 – fc) wobei
ni die Anzahl der auf der Skala gemessenen Teilungen ist,
nm = Gesamtzahl der Teilungen der Skala,
fr = relative Frequenz,
fc = die kleinste gemessene relative Häufigkeit.
Der Gesamtstromverbrauch beträgt 12 mA bei 12 V, wenn die LC-Messung erfolgt.
elektor 84436-11
Ein LC-Meter oder Indictance/Capacitance Meter ist ein Mehrzweck-Messgerät, das zur schnellen Identifizierung unbekannter Induktor- und Kondensatorwerte verwendet wird. Ein LC-Meter ist ohne Zweifel unerlässlich für jeden, der mit elektronischen Schaltungen zu tun hat.
Die erläuterte Schaltung nimmt die unbekannte Induktivität La oder Kapazität CO innerhalb einer 2-Transistor-Oszillatorschaltung auf, in der die Ausgangsspannung durch einen Regler konstant zwischen 30 und 40 mV gehalten wird.
Wenn in der Oszillatorschaltung Ca parallel mit dem Kondensator Co. oder La in Reihe mit der Induktivität L0 angeschlossen ist, nimmt die Frequenz der Schaltung ab.
Diese Verringerung wird durch einen Frequenz-Spannungs-Wandler T3/T4 bewertet.
Die resultierende Ausgangsspannung des Emitterfolgers T5 wird verwendet, um das Messgerät M1 zu stimulieren.
Der Zähler M1 ist an den Diagonalen einer Brückenschaltung angeschlossen, damit er Null anzeigt, wenn Ca oder La nicht vorhanden sind.
Das Messgerät ist auf die Skalenendwertanzeige f.s.d.1 bis P2 fixiert, falls entweder La = Lo oder Ca = Co in die Oszillatorschaltung eingeführt wird.
Die Schwelle des frequenzbestimmenden Kondensators CL im Frequenz-Spannungs-Wandler wird durch P1 ausgeglichen.
Daher ist es zwingend erforderlich, für jeden einzelnen Messbereich mit einem neuen 10 k-Preset umzuschalten, und jedes Mal, wenn dies durchgeführt wird, wird der f.s.d. muss mit P2 neu fixiert werden.
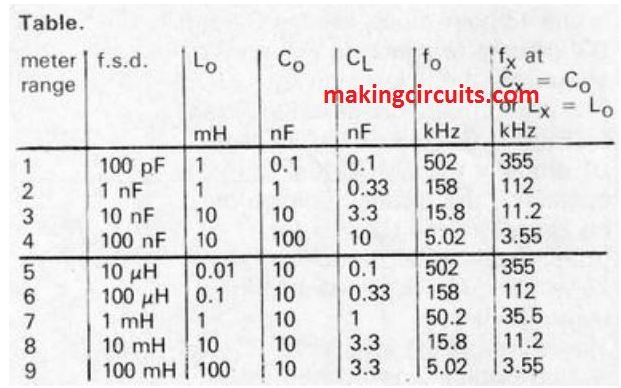
Die in der Schaltung gelieferten Größen für Lo und Co sind für einen f.s.d. von 10 nF oder 10 m1-1.
Eine Höchstzahl von 9 Testbereichen könnte von einem 4-Wege-Drehschalter mit 9 Positionen verfügbar gemacht werden.
Die Beträge von L., Co CL und die entsprechende Frequenz, ohne Lx oder C und bei Vollausschlag, sind in der Tabelle aufgeführt.
Die Genauigkeit der Messwerte liegt bei vorsichtiger Kalibrierung bei ca. 3 %.
Die Markierungen des Bereichs sind für alle Bereiche nahezu ausreichend gleich, werden jedoch für niedrigere Messungen um ein Element von etwa 3 "erweitert".
Dies bedarf natürlich einer entsprechenden Korrektur.
Das Kalibrieren der Waage kann mit einer Tabelle durchgeführt werden, die mit der Formel ni = nm(1-fr)/(1-fc) erstellt wurde, wobei:
ni = Anzahl der angezeigten Skalenteile
nm = Anzahl der Skalenteilungen bei FSD
fr = relative Häufigkeit
fc = niedrigste relative Frequenz
Gesamtstromaufnahme beträgt ca. 12 mA bei 12V,
Quelle:
https://www.electroschematics.com/lc-meter-coil-capacitor-meter/
https://makingcircuits.com/blog/simple-lc-meter-circuit-for-measuring-inductance-and-capacitance-at-home/
x516_c_2L3D-5T-1Ins-12V_84436-11 BC550C LC Messgerät 10uH bis 100mH und 100pf bis 100nF_1a.pdf
********************************************************I*
Simple LC Meter
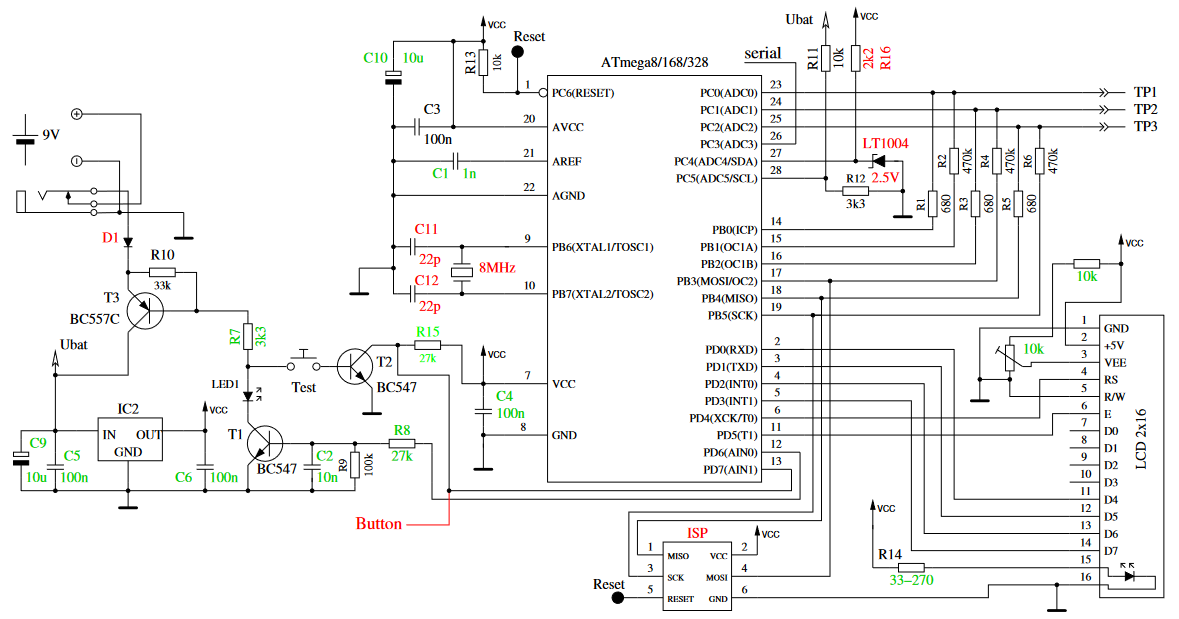
Measure inductance and capacitance with Platino Einfaches LC-Meter elektor Induktivität und Kapazität mit Platino messen
Elektor 5/2018 Seite 38
elektor 130341-11
Beschreibung:
Die Zusatzplatine besteht aus einer Schaltung zum Erzeugen einer Resonanzfrequenz zum Messen der Induktivität
und einer Opamp-Schaltung zum Erzeugen einer Frequenz basierend auf dem Laden und Entladen der zu messenden Kapazität.
Diese Frequenzen werden dann von der Software gelesen, um die Induktivität und Kapazität der angeschlossenen Komponente zu bestimmen.
LCD-Display und Drehgeber für die Anzeige und Benutzerschnittstelle sind ebenfalls vorhanden.
Spezifikationen:
DC-Eingang: 12V bis 15V DC
Elektor Platino mit Mikrocontroller ATMEGA328P.
16 x 2 LCD-Anzeige
Induktivitätsbereich 10uH bis 1H
Kapazitätsbereich 47pF bis 10uF
Merkmale:
Automatische Bereichsauswahl.
Drehgeber zur Auswahl des Induktivitäts- und Kapazitätsmodus.
Induktivitäten und Kondensatoren sind zwei Arten von Komponenten, die einiges gemeinsam haben, sich jedoch sehr unterscheiden.
Zum Beispiel können beide Energie speichern, obwohl sie von der Induktivität als magnetisches Feld gespeichert wird, während ein Kondensator elektrische Ladung speichert.
Eine weitere Gemeinsamkeit besteht darin, dass es schwer ist, ihren genauen Wert zu kennen.
Viele Multimeter können die Kapazität messen (C in Piko-/Nano-/Mikro-/Milli-Farad), aber nur wenige die Induktivität (L in Mikro-/Milli-Henry).
Sie müssen ein L-Meter kaufen, um Induktivitäten zu messen.
L-Meter messen normalerweise auch Kapazität und Widerstand und werden daher oft als LCR-Meter bezeichnet.
Wir beschränken uns auf L & C und überlassen den Widerstand dem treuen Multimeter.
Schaltungen lassen sich häufig durch Mikrocontroller vereinfachen.
Das gibt es allerdings nicht umsonst:
Was beim Schaltplan weggelassen wird, muss durch Software kompensiert werden.
Allerdings erhält man so wesentlich flexiblere Hardware.
Dies gilt auch für das folgende kleine Projekt, bei dem Induktivität und Kapazität mit einem Mikrocontroller und einigen zusätzlichen Bauteilen elegant gemessen werden.
Quelle: https://www.elektormagazine.de/magazine/elektor-201805/41487
https://www.elektormagazine.de/labs/platino-based-simple-lc-meter-130341
https://www.elektormagazine.com/magazine/elektor-201805/41545
********************************************************I*
ELV ESR-Messgerät ESR 1
Das Messgerät ermittelt den Ersatz- Serienwiderstand (ESR) eines Elektrolyt- Kondensators (kurz: Elko) - dies sogar im eingebauten Zustand.
Der ESR gibt Aufschluss über den Alterungszustand bzw. die „Qualität“ eines Elkos.
Speziell in Schaltnetzteilen altern Elkos, bedingt durch die hohe Schaltfrequenz bzw. hohe Arbeitstemperaturen, schneller als „normal“.
Steigt der ESR eines zur Spannungssiebung eingesetzten Kondensators über einen bestimmten Wert an, kann unter Umständen die Funktion des Schaltnetzteiles gestört werden.
Selbstverständlich kann das ESR 1 auch zur Messung von ohmschen Widerständen im angegebenen Messbereich verwendet werden.
Wird ein Elko mit der maximal zulässigen Betriebstemperatur eingesetzt, beträgt die durchschnittliche Lebensdauer 1000 bis 3000 Betriebsstunden.
Allein schon die Lagerung bewirkt einen stetigen Kapazitätsverlust, sodass nach ca. 10 Jahren Lagerzeit ein Elko nicht mehr verwendet werden sollte.
Einer der wesentlichen Gründe hierfür ist, dass das flüssige Elektrolyt im Inneren des Elkos mit der Zeit austrocknet (verdunstet).
Maßgeblich entscheidend für den Austrocknungsprozess ist die Betriebstemperatur, die von der Umgebungstemperatur und der vom Elko selbst erzeugten Wärme bestimmt wird.
In modernen Schaltnetzteilen werden die eingesetzten Elkos extremen Belastungen ausgesetzt.
Durch die relativ hohe Schaltfrequenz und die hohen, zum Teil rechteckförmigen Impulsströme erwärmen sich die Elkos, wodurch die Lebensdauer rapide absinkt.
Nicht umsonst sind Netzteile in Computern eine der häufigsten Ausfallursachen.
Solche Schaltnetzteile finden zunehmend aber auch Einzug in moderne Consumergeräte.
Hierbei ist ein Trend zu beobachten, dass viele dieser elektronischen Geräte wie z. B. Fernseher, Videorecorder, Monitore usw. heute schon nach relativ kurzer Zeit ausfallen. Als Fehlerursache stellt sich oft ein defekter Elko im Schaltnetzteil heraus.
Misst man solche Elkos mit einem Kapazitätsmesser nach, stellt man erstaunt fest, dass diese nur unwesentlich an Kapazität verloren haben.
Der Innenwiderstand des Kondensators, auch ESR (Equivalent Series Resistance) genannt, ist allerdings angestiegen.
Bei hohen Frequenzen wirkt der ESR zusammen mit der Kapazität wie ein Tiefpass und setzt so die Wirkung der realen Kapazität deutlich herab.
Dies hat zur Folge, dass wie schon erwähnt, ein Schaltnetzteil z. B. nicht mehr einwandfrei arbeitet.
Mit dem ESR-Messgerät kann der Innenwiderstand (ESR) eines Elkos in der Schaltung gemessen werden, ohne diesen auslöten zu müssen.
Hierdurch wird das lästige und zeitraubende Auslöten mit dem anschließenden Messen der Kapazität vermieden.
Zudem ist in solchen Fällen der ESR aussagekräftiger als die mit einem Kapazitätsmessgerät gemessene Kapazität.
Zusätzlich kann das ESR 1 auch zur Messung von ohmschen Widerständen bis 19,99 Ohm verwendet werden.
Das handliche Messgerät ist durch Batteriebetrieb (9-V-Blockbatterie, nicht im Lieferumfang) sehr gut auch im mobilen Service einsetzbar.
Die Low-Bat- Anzeige warnt rechtzeitig vor erschöpfter Batterie.
Quelle:
https://de.elv.com/elv-esr-messgeraet-esr-1-052699?
********************************************************I*
Handheld LCR Tester
DER EE DE-5000 Handheld LCR Meter DER EE LCR METER DE-5000 Der-EE DE-5000 LCR Meter 100 kHz
Quelle:
https://de.deree.com.tw/lcr-meter.htm https://de.deree.com.tw/de-5000-lcr-meter.html https://www.deree.com.tw/de-5000-lcr-meter.html https://de.deree.com.tw/de-5000.html https://www.eleshop.nl/de-ree-de-5000-lcr-meter.html https://eleshop.eu/de-ree-de-5000-lcr-meter.html Messen mit dem LCR Meter DE 5000 Teil 1 https://www.youtube.com/watch?v=Qb3EWRCp4kM Messen mit dem LCR Meter DE 5000 Teil 2 https://www.youtube.com/watch?v=TxI5uW3U4zU
Part - 1 Intro
Part –2) L (inductance), C (capacitor), R (resistance), few thoughts. Part – 3) DE 5000 LCR specifications Part - 4) What is in the box? Part - 5) DER EE, DE 5000 VS Agilent U1733C (all around comparison) Part - 6) Plus and minus of the design and in relation with LCD resolution. Part -7) Software PC connectivity & Over all experience Part 8) Conclusion
ITTSB Blog
https://www.ittsb.eu/DER-EE-DE-5000-LCR-Meter-Review.html
********************************************************I*
Andere Handheld LCR Meter
Der EE DE-5000 High Accuracy Handheld LCR MeterDER EE DE-5000 Smart LCR Meter
TH2822M
ST2822A LCR Messgerät € 249,- ST2830
CEM LCR-Messgerät DT-9935
EXTECH 380193 Passiv Component LCR meter
PROSER BM4070 UNI-T UT603 Digitales LCR-Messgerät € 29,99 UNI-T UT603 LCR-Meter € 36,- UNI-T UT612 LCR-Meter € 123,93 Keysight E4980A ESR GZ84808 PeakTech 2170 PeakTech 2175 LCR-Meter, digital, 11000 Counts € 84,91 PeakTech 2180 Digitales Multimeter mit LCR-Meter € 102,65 PeakTech P 3730 PeakTech 5105N Hantek-1832C Handheld 40kHz LCR Meter Hantek-1833C LCR Elite2 RS PRO RS-9935 LCR-Messgerät, Handgerät, 100kHz
********************************************************I*
UDB1002 SeriesJUNTEK UDB 1008S UDB1008S
UDB1000 Series 1008S DDS Signal Source Signal Generator with 60MHz Frequency Meter Sweep Module
********************************************************I*
Digital LCD LC100-A haute précision Inductance Capacitance L/C Meter Testeur
Alice1101983 LC100-A LC100-A High Precision Digital Inductance Capacitance L/C power Meter module LC100-A LCR Digital Meter Inductimetro Capacimetro Itytarg LC100-A LC Meter 1uH-100H Induktivität 1pF-100mF Kapazität
Hersteller: CTRLZS
Original LC-100A LC Meter Digial Induktivität Kapazität Prüfung Modul mit LCD Display € 24,56
LC 100A LCD LCD Kapazitätsmesser LC Meter 1pF 100mF 1uH 100H Wooge Induktivitäts und Kapazitäts LC-Meter LC100-A 500297001 G 04-09-0304 33374-TE
LC-100A LCD Kapazitätsinduktivitätsmesser LC-Meter 1pF-100mF 1uH-100H € 20,10 1 Stk. vorhanden
KNACRO LC100-A Digitales LCD Hochpräzise Induktivität Kapazität L C Meter Genauigkeit 1%
Fügt eine präzise Messung eines Hochgeschwindigkeits-Mikrocontrollers hinzu, der für Mikrowellen- und Schaltnetzteiltransformatoren geeignet ist.
LC100-A
https://de.aliexpress.com/item/32829227933.html
ProduktbeschreibungenBedienungsanleitung:
https://www.amazon.com/clouddrive/share/c355trs2BExdtnWkaVmW7saJYykKKHMCgEMKCpUcCdJ
User's manual of LC100A.pdf
300_b_Wooge-x_LC100-A Protable Meter - User's manual of LC100A_1a.pdf
Basierend auf dem L/C-Resonanzprinzip.
Präzisionsberechnung des Hochgeschwindigkeits-Mikrocontrollers. Messbereich unter 1 uH und 1 pF Besonders geeignet in der Mikrowelle und Messung von Schaltnetzteil-Transformator, Filterinduktivität LC100-A hat vier Messbereich-Positionen: 1. C-Bereich: Kapazität (0,01pF-10uF) 2. L-Bereich: Induktivität (0,001 uH-100 mH) 3. Hi.L-Bereich: Große Induktivität (0,001 mH-100 H) 4. Hi.C-Reichweite: großer Kapazitätsbereich (1uF-100mF) Technische Daten: Kapazitäts-Genauigkeit: 0,01pF-1pF: 5% 1pF-1uF: 1%. 1uF-10uF: 5% Minimale Kapazitäts-Auflösung (C-Dateien): 0,01 pF Induktivitäts-Genauigkeit: 0,001uH-1uH: 5% 1uH-100mH: 1%
Induktivitätsmessung (L): Genauigkeit: 1uH~100mH 1%
Minimale Induktivitäts-Auflösung (L-Dateien): 0,001 uH
Große Induktivitäts-Genauigkeit: 100mH-1H 1% 1H bis 100H 5%
Große Induktivitätsmessung (Hi.L): Genauigkeit: 100mH~1H 1%; 1H bis 100H 5%
Min. Auflösung großer Induktivität (HL-Dateien): 0,001 mH
Genauigkeit: 1uF-100mF-5%
Große Kapazitätsmessung (Hi.C): Genauigkeit: 1uF~100mF 5%
Minimale Auflösung der großen Kapazität (HC-Dateien): 0,01 uF
Frequenz: L-Dateien, C-Dateien: Abt. 500 kHz HL Dateien: Abt. 500 Hz
Testfrequenz: L/C: 500 kHz
Hi.Lo: 500Hz bis 50KHz
Messmodus für Induktivität/Kapazität/große Induktivität: LC-Resonanz
Messmodus für große Kapazität: Laden und Entladen
Anzeige: 1602 LCD
Anzeigestellen: 4-Stellen Stromversorgung Schnittstelle: Mini-USB 5V DC-Buchse Versorgungsspannung: 5Vdc Lieferumfang: 1 x LC100-A Digitales L/C Messgerät Induktivität Kapazitätsmesser 1 x Mini-USB-Kabel 1 x LC100-A Bedienungsanleitung (evtl. nicht in deutscher Sprache)
Hier ist eine Bedienungsanleitung ohne Schaltplan:
Hier baut ein FA einige Mods ein, aber nichts Relevantes in Bezug auf die Messfunktion:
https://vk4ghz.com/lc100-a-lc-meter-mods/
LC100-A LC Meter geht nicht so ganz https://www.mikrocontroller.net/topic/505032
300_b_Wooge-x_LC100-A Digital L-C-Meter - Inductance Capacitance Meter - User Manual_1a.pdf 300_b_Wooge-x_LC100-A LC-Meter - Induktivitäts und Kapazitäts Messgerät - Schaltplan_1a.png300_b_Wooge-x_LC100-A LC-Meter - Induktivitäts und Kapazitäts Messgerät - User-Manual_1a.doc https://www.amazon.de/KNACRO-Digitales-Hochpr%C3%A4zise-Induktivit%C3%A4t-Genauigkeit/dp/B06XSD9VN1
https://www.amazon.de/Dehumi-Induktions-Kapazit%C3%A4t-Kondensator-1Pf-100Mf/dp/B0BBQ9VRKB/ref=mp_s_a_1_7?
https://www.ebay.de/itm/195325760610?mkevt=1&mkcid=1&mkrid=707-53477-19255-0&campid=5338906311&toolid=20006&customid=255_255_255&
https://www.amazon.de/CTRLZS-Induktivit%C3%A4Ts-Kapazit%C3%A4Ts-LC-Meter-Digital-Kondensatormessger%C3%A4T-LCD-Kapazit%C3%A4Tsmessger%C3%A4T-Mini-USB-Schnittstelle/dp/B0BFKYW7S2
LC-Meter-Modul BC-003
FUNK AMATEUR LC-Meter-Modul BC-003
JUNCTEK LC 100A LC-100A
LC-100A Digital L/C Meter Induktivität Kapazität Tester Palette 0,01 pF zu 10uF LCD DisplayLC-Meter-Einbaumodul mit beleuchtetem LC-Display,LC100-A LC Meter 1uH-100H Induktivität 1pF-100mF Kapazitätstabelle
Technische Daten:
Kapazitätsmessbereich 0,01 pF bis 10 µF
Induktivtätsmessbereich 1 nH bis 100 mH (mit hoher Messfrequenz) Induktivtätsmessbereich 1 µH bis 100 H (mit niedriger Messfrequenz)
LC-Display 2 x 16 (beleuchtet)
Auflösung 4 Digits
Betriebsspannung 5 V (über USB- oder DC-Buchse)
Stromaufnahme 20 mA (etwa
Abmessungen 81 mm x 47 mm x 30 mm
Neil Heckt, Inhaber der US-Firma
AADE www.aade.com Kurzbedienungsanleitung [PDF-Dokument] 3-D-Druckdateien für LC-Meter-Gehäuse mit Messleitungen [ZIP-Datei] 3-D-Druckdateien für LC-Meter-Gehäuse mit Anschlussbuchsen [ZIP-Datei]
Quelle:
http://68.168.132.244/LC100A_EN_manual.pdfhttps://chat.whatsapp.com/CBXHIjh1CdpE5OBwUfchLi
300_b_fritz-x_LC-Meter-Modul BC-003 - Datenblatt_1a.pdfhttps://www.mikrocontroller.net/topic/504964
https://www.box73.de/product_info.php?products_id=2561
LC-Meter-Projekt mit ATmega
Quelle:
https://www.mikrocontroller.net/topic/504964
https://www.mikrocontroller.net/topic/504964
300_b_fritz-x_LC-Meter SCM Bartels AutoEngineer CAE - Schaltplan_1a.pdf
LCR 2.9C bridge / meter kit measures L/C/R/Z/Rs/ESR/X/Q/D/Phase angle, in-circuit C/ESR
https://www.youtube.com/watch?v=ZQ33AR1ffFI https://www.youtube.com/watch?v=BGjV5vUvGPchttp://electronoobs.com/eng_arduino_tut10_3.php
Verdrahtungsplan:
http://electronoobs.com/images/Arduino/tut_10/Inductance_meter_on_breadbord.png
INI BUKAN ESR METER/SMART TESTER
********************************************************I*
https://pe2bz.philpem.me.uk/Comm01/-%20TestEquip/-%20Tester-NonActiveDevice/Cl-251-IndCap-MeterKit/lc-meter-project.htm
Fa.
Almost All Digital Electronics
mailto:[email protected]http://www.aade.com Handheld LC Meter 1pF-100mF Digital LCD Capacitance Meter Inductor Table € 40,- LC-200A Handheld Inductance Capacitance Meter Inductor Capacitor Tester Kit New LC Meter 1pF-100mF 1uH-100H LC200A Digital Capacitance Meter Capacitor Table LCR-Messgerät, Induktivitätskapazitätsmesser, Kapazität Multimeter Handheld L/C-Messgerät, LC-200A Elektrisches ABS LCR Multimeter LC-200A Hohe Präzision Induktivität Kapazität Meter Handheld Induktivität Meter Kapazität Meter LC Digitale Brücke Tester
LC200A Portable LC Meter
C-Bereich: 1pF-10uF
Kapazitätsgenauigkeit: 1%(1pF~1uF), 5%(1uF~10uF)
Großer C-Bereich: 1uF-100mF
Große Kapazitätsgenauigkeit: 5% (1uF-100mF)
Messauflösung großer Kapazität (Hi.C-Bereich): 0,01uF
L-Bereich: Induktivität (1uH-100mH)
Induktivitätsgenauigkeit: 1% (1uH ~ 100mH)
Messauflösung der Induktivität (L-Bereich): 0,001uH
L-Bereich: Große Induktivität (0,001 mH-100 H)
Genauigkeit der großen Induktivität: 1% (100mH~1H), 5%(1H~100H)
Messauflösung großer Induktivität (Hi.L-Bereich): 0,001 mH
Messmethode für große Kapazitäten: Laden-Entladen
Anzeige:1602LCD
Effektive Anzeigeziffern: 4 Ziffern
Schnittstelle zur Stromversorgung: Mini USB/Φ5.5DC Buchse, 4x AA Batterie
Versorgungsspannung: 5V
Material: Elektronische Komponente
Größe: 150x89 mm
300_b_BRT-x_BRT LC200A LC-Meter V5.0 - User-Manual_1a.pdf
300_b_BRT-x_BRT LC200A LC-Meter - User-Manual_1a.pdf
www.brightwinelectronics.com https://www.walmart.com/ip/1pc-Handheld-LC-Meter-1pF-100mF-Digital-LCD-Capacitance-Meter-Inductor-Table/794221513?wmlspartner=wlpa&selectedSellerId=101110496 XJW01 digitale brücke 0.3% LCR tester widerstand, induktivität, kapazität, ESR,
Cp:Kondensator in parallelModus Cs:Serie kondensatorModell Lp: inductorIn parallel modus Ls:Serie inductorModell Rp:Widerstand in parallelModus Rs:Widerstand in serieModell Stellvertretender SenatsDisplay: Die qualität faktor Q D:VerlustFaktor Theta:Phase winkel Rp:Äquivalent parallel widerstand ESR:Equivalent series widerstand Xp:Äquivalent shuntReaktanz Xs:Equivalent series reaktanz Fuction Test parameter L, C, R, D, Q, ESR Grund genauigkeit 0.3%-0.5% Ersatzschaltung Serie Palette Modus Auto Test Geschwindigkeit Schnell: 2,5, medium: 2, Langsam: 1 (mal/sec.) Kalibrierung Funktion Auto Test terminal konfiguration DieBNCTest linie Display 2004 LCD Test signal Test signal frequenz 100Hz, 1 kHz, 7,831 kHz Test signal level 1,75 Vrms (max) Test Palette
R 0,0002 Ω-9,999 MOHM
C 0,1 pF-10000 uF oder mehr L 0,01 μH-1000 H D, Q 0,001-9999 https://de.aliexpress.com/item/32953590786.html?
********************************************************I*
Banggood
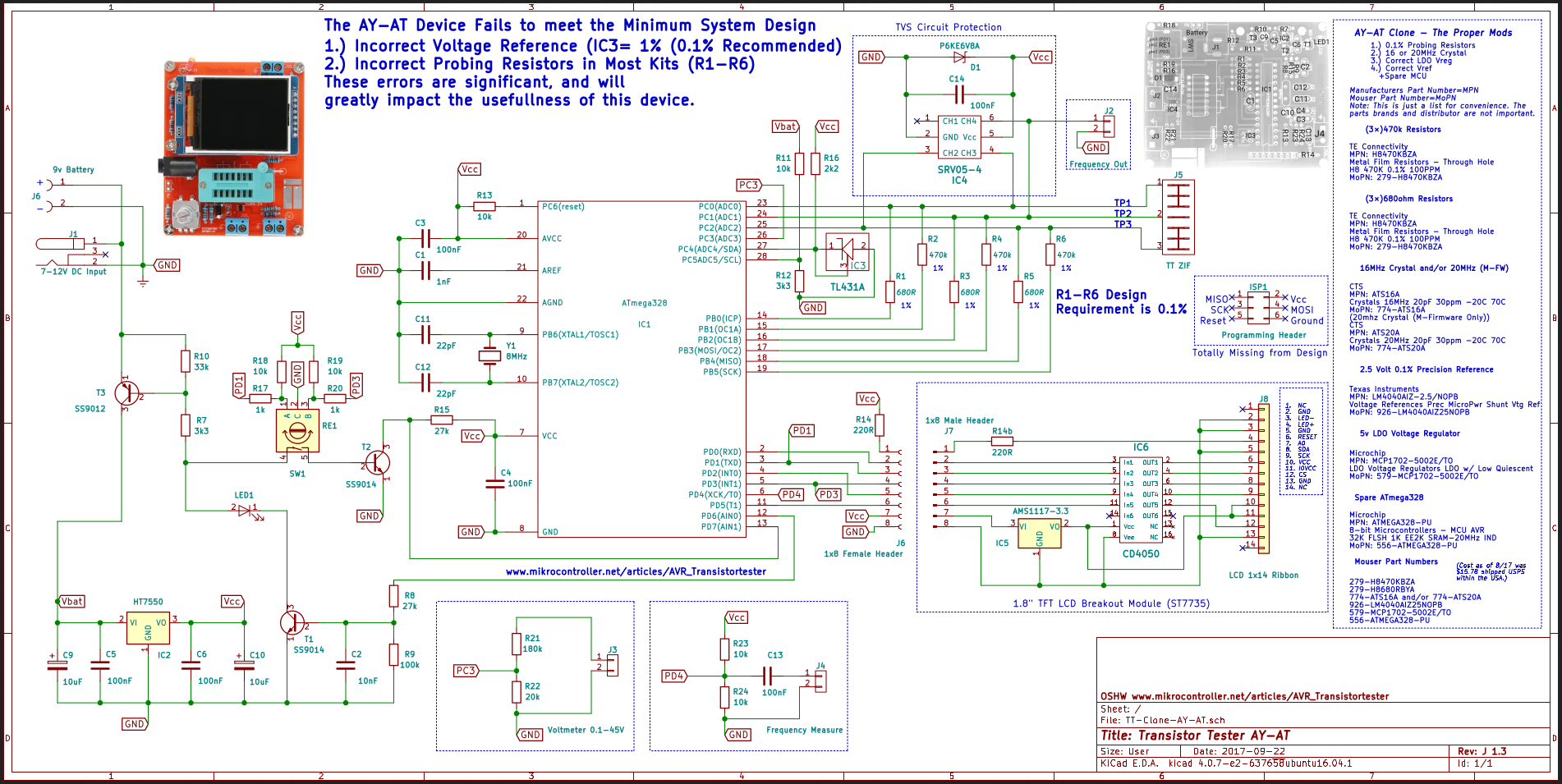
I have the GM328 kit from Banggood. It's usually called AY-AT instead, as it's not really a GM328.
Transistortester GM328 aus China Multifunktionale LCD GM328 Transistor Tester
Diodenkapazität ESR Spannung Frequenz Meter PWM Rechtecksignal-Generator
GM328A LCD Transistortester-Diode ESR-Messgerät PWM Gelötetes Modul des Rechteckgenerators € 16,87
DollaTek
GM328A LCD-Transistortester-Diode ESR-Messgerät PWM-Rechteckgenerator-Lötmodula Multifunktionale LCD GM328 160x128 LCD Display Transistor Tester ESR Meter Cymometer Square Wave Generator
Der GM328 Transistor-Tester, der wohl auf dem OpenSource-Projekt von Markus Frejek basiert und weiterentwickelt wurde.
https://www.mikrocontroller.net/articles/AVR_Transistortester
https://github.com/blurpy/transistor-tester
Mit diesem Gerät können wir den Wert eines Widerstandes ermitteln, Kondensatoren, Thyristoren, Triacs, Transistoren (NPN- und PNP-Transistoren), N- und P-Kanal MOSFETs, JFET und Dioden.Die Pin-Belegung der Bauteile wird automatisch ermittelt und auf dem LCD angezeigt. Neben den bedrahteten Bauteilen ist es auch möglich, SMD-Bauteile bequem messen zu können. Das Gerät hat zusätzlich noch drei Kabel, mit denen wir ebenfalls Bauteile messen können. Die Genauigkeit ist recht hoch und in einem Menü gibt es noch weitere Funktionen zur Auswahl wie Frequenzmessung, Spannungsmessung, usw. Das GM328 braucht eine 9V-Blockbatterie zum Betrieb und kann mit nur einem Knopf ganz leicht bedient werden. Die meisten Bauteile werden in unter 2 Sekunden gemessen. Ich habe für meines einfach mit zwei Plexiglasscheiben, eine rote Tastenkappe mit Sprungfeder aus einem Kuli, Schraubenabstandshaltern, acht Schrauben und 16 Muttern ein kleines offenes Gehäuse drum herum gebaut.
Es gibt aber auch für etwas mehr Geld eines mit Gehäuse zu kaufen.
Das Schöne ist, wenn man unsortierte Bauteile wieder wegräumen möchte. Keine Farbcodes entziffern mehr. Was auch sehr nützlich ist, ist die oben angesprochene automatische Pin-Belegung: “Wo war nochmal der Collector beim BC 548B? Linkes Bein, oder rechtes Bein?” Kein Problem. Einfach den Transistor in die Prüfvorrichtung gesteckt und ausmessen lassen.
Quelle:
https://www.kollino.de/elektronik/gm328-transistor-tester/
Der Prozessor verwendet den leistungsstarken Einzelchip ATmega328P DIP-28. Mit IC-Sitz. Die Anzeigeeinheit verwendet eine Farbanzeige mit 160 x 128 Pixel, die Zeichennummer des gesamten Bildschirms beträgt 8x20, die Farbtiefe beträgt 16 Bit und das Symbol der Grafikanzeigekomponente. Drehschaltersteuerung, Ein-Knopf-Messung, automatische Abschaltung. Es wird von einer 9V Laminatbatterie gespeist und kann auch von einem Netzteil gespeist werden.
Der Strom beträgt ca. 30mA und der Strom beträgt nach dem Herunterfahren ca. 20nA.
Automatische Erkennung von NPN- und PNP-Transistoren, FETs, Dioden, Doppeldioden, Thyristoren, Thyristoren, automatische Identifizierung der obigen Transistor-Pin-Verteilung.  a aDC-Spannungsmessung : bis zu 50V Capacitor : 1pF resolution, 25pf - 100,000 uf Resistance : 0.1 ohm resolution, maximum 50M ohm Digital 160 * 128 LCD-Display für einfache Messwerte, können Messdaten und Grafiken anzeigen. Multifunktionaler Transistor-Tester zur automatischen Erkennung von NPN- und PNP-Transistoren,
FET, Dioden, Dual-Dioden, Thyristoren, SCR,
automatische Identifikation der Transistor-Pinbelegung.
Auch kann als quadratisches Signal und PWM-Signalgenerator verwendet werden.
https://github.com/blurpy/transistor-tester
https://raw.githubusercontent.com/blurpy/transistor-tester/master/resources/AY-AT-J1.3.png https://github.com/blurpy/transistor-tester/blob/master/resources/gm328-kit.jpg https://www.mikrocontroller.net/articles/AVR_Transistortester
Messgerät
Joy-iT, LCR-T7 , Transistortester € 21,95 JOY-iT LCR-T7 Multi-funktions Tester T7 MultifunktionsTester
elektor 13. Juli 2021
Messgerät, Joy-iT, LCR-T7 , Transistortester
Beschreibung Dieses LCR-Meter bietet eine Vielzahl an Funktionen für einen kleinen Preis.
Das LCR-Meter kann unter anderem Kapazitäten, Widerstände und Induktivitäten messen.
Außerdem kann es automatisch Bauteile erkennen, so kann es zum Beispiel verschiedene Transistorarten, wie NPN- oder PNP-Transistoren unterscheiden.
Das Gerät ist besonders leicht zu bedienen, da alle Messungen mit nur einem Knopfdruck gestartet werden.
Durch den integrierten 350mAh Akku, können auch unterwegs Messungen durchgeführt werden. Der Akku wird mit Hilfe eines 5V Netzteils (separat erhältlich) und dem beiliegenden microUSB-Kabel geladen. Zudem kann dieses Messgerät Infrarot-Signale entschlüsseln und in einer Wellenform auf dem Display anzeigen.
Dieses Messgerät ist in der Lage Dioden, Z-Dioden, Doppeldioden, Widerstände, Kondensatoren, Induktoren, Thyristoren, Triacs, Feldeffekttransistoren, Bipolartransistoren und Batterien zu erkennen und auszumessen.
Außerdem kann es automatisch Bauteile erkennen.
So kann es zum Beispiel verschiedene Transistorarten, wie NPN oder PNP Transistoren unterscheiden. Das Gerät ist besonders leicht zu bedienen, da alle Messungen mit nur einem Knopfdruck gestartet werden.
Durch den integrierten 350 mAh Akku, können auch unterwegs Messungen durchgeführt werden.
Der Akku wird mit Hilfe eines 5V Netzteils (separat erhältlich) und dem beiliegenden microUSB-Kabel geladen.
Zudem kann dieses Messgerät Infrarot-Signale entschlüsseln und in einer Wellenform auf dem Display anzeigen. Messbare Komponenten: Widerstand, Kondensator, Induktor, Thyristor, Triac, (Doppel-)Diode, Z-Diode, Feldeffekttransistor, Bipolartransistor, Infrarot-Decoder (Hitachi-Codierung) Unterstütztes IR-Protokoll: NEC (wird von vielen Herstellern verwendet)
Display: 1,8" 3,5-Inch TFT-LCD (160x128 Pixel)
Besonderheiten:
Automatische Kalibrierung
Ein-Tasten-Bedienung
Eingebauter Akku: Lithium-Ion-Akku 3,7V / 350mAh
Abmessungen: 90x70x2 mm Lieferumfang: Messgerät, Messklemme, Micro-USB-Kabel, LED, Kondensator Messbereich Kapazität: 25 pF - 100 mF Widerstand: 0,01 - 50M Ohm Induktivität: 0,01 mH - 20 Henry Akku: 0,1 - 4,5 V, 300 mAh (eingebauter Lithium-Ion-Akku 3,7 V, 350 mAh)
Z-Diode Durchbruchspannung: 0,01 - 30 Volt
Z-Diode: 0,01 - 4,5V Diode Uf < 4,5V Thyristor / Triac IGT < 6 mA Lieferumfang
Messgerät, Messklemme, micro-USB-Kabel, LED, Kondensator
Multifunktionsmessgeräte sind bei diskreten Bauelementen immer ein Nice-to-have, sowohl für passive als auch für aktive Bauteile. Manchmal sind Werte oder Typennummern schwer ablesbar und bei diskreten Halbleitern mit exotischen Typennummern wollen Sie vielleicht prüfen, um welche Art von Bauteil es sich handelt. Und selbst wenn Sie das Teil visuell identifizieren können, möchten Sie vielleicht wissen, ob es noch funktioniert und ob es - bis zu einem gewissen Grad - seinen ursprünglichen Spezifikationen entspricht. Hier kommt ein Tester wie der JOY-iT LCR-T7 ins Spiel:
eine schnelle Überprüfung, um welches Bauteil es sich handelt, oder zumindest zu sehen, ob es das Teil ist, von dem man es erwartet.
Mit anderen Worten, mit dieser Art von Ausrüstung ist es einfach, diskrete Komponenten zu testen, zu identifizieren, um welche Art von Teil es sich handelt und - im Falle von Halbleitern - sogar herauszufinden, was das richtige Pinning ist. Wie der Name schon sagt, handelt es sich um einen Tester, erwarten Sie also nicht, dass Sie von diesem Gerät hochgenaue Messungen erhalten. Das sollte man auch nicht von einem Messgerät verlangen, das weniger als drei Zehner kostet. Eines der schönen Dinge am LCR-T7 ist, dass er sehr einfach zu bedienen ist: Einfach den Prüfling an die ZIF-Buchsenleisten auf der Frontplatte anschließen, entweder mit oder ohne die mitgelieferten Drähte und Clips, und den Startknopf drücken. Das war's.
Das Gerät erkennt automatisch, welche Art von Bauteil angeschlossen ist und zeigt dessen Hauptparameter und Pinning (falls zutreffend) auf der LCD-Anzeige an.
Das Joy-iT LCR-T7 Messgerät bietet Ihnen eine Vielzahl an Funktionen zu einem attraktiven Preis.
Mit Hilfe unseres LCR Messgerätes können Sie die Induktivitäten ( L ) von Spulen, Kapazitäten ( C ) von Kondensatoren und deren Widerstände ( R ) als Verlust messen.
Die automatische Bauteilerkennung unseres Messgerät kann elektronische Komponenten ( Dioden, Z-Dioden, Doppeldioden, Widerstände, Kondensatoren, Induktoren, Thyristoren, Triacs, Feldeffekttransistoren, Bipolartransistoren und Batterien ) erkennen und zum Beispiel zwischen verschiedenen Transistorarten ( NPN oder PNP ) unterscheiden.
Die Messungen werden automatisch durch einfachen Knopfdruck gestartet. Mit dem integrierten Infrarot-Decoder können sogar Infrarot-Signale entschlüsselt und auf dem Display in Wellenform und Hexadezimal-Code angezeigt werden.
Dank des integrierten 350mAh Akku kann das Messgerät mobil eingesetzt werden.
Mit Hilfe des beiliegenden microUSB Kabels und diversen USB Stromquellen ( z.B. 5V Netzteil, Powerbank, PC und vieles mehr ) kann der Akku wieder aufgeladen werden.
Handbuch 300_b_JOY-iT-x_JOY-iT LCR-T7 Multi-Funktions-Tester, Transistortester - Anleitung 2021_1a.pdf 300_b_JOY-iT-x_JOY-iT LCR-T7 Multi-Funktions-Tester, Transistortester - Datenblatt_1a.pdf
https://www.elektormagazine.de/articles/joy-it-lcr-t7-multi-funktions-tester?
https://joy-it.net/files/files/Presse/LCR-T7_Elektor-Magazin_2021-07-13.pdf https://joy-it.net/de/products/JT-LCR-T7 https://www.pollin.at/p/messgeraet-joy-it-lcr-t7-transistortester-830961 https://www.conrad.at/de/p/joy-it-transistortester-2355021.html https://www.elektor.de/joy-it-lcr-t7-multi-function-component-tester
********************************************************I*
L-C Meter im Eigenbau LC Messgerät als Eigenbauprojekt
Vom Herr Nussbaum beschriebenen LC-Meter.
Es handelt sich dabei um ein digital anzeigendes L-C Messgerät mit einem sehr günstigen Kosten - Nutzen Faktor.
Ohne Gehäuse belaufen sich die Bauteile auf ca. 10,- bis max. 20,- Euro, je nachdem wo man einkauft.
Die teuersten Bauteile sind das LCD - Display (1x16 Zeichen genügt) und der Mikrocontroller PIC16F84. Günstige Displays gibt es aber zum Beispiel bei: www.neuhold-elektronik.at (1,95 Euro).
Die anderen Bauteile dürften bei einem Bastler wohl in der Krabbelkiste zu finden sein.
Der Messbereich erstreckt sich von 0,1pF bis 1,0uF für Kondesatoren und von 0,1nH bis 100mH für Spulen.
Die Genauigkeit liegt im Bereich von +/-1%, was mich für die Einfachheit dieses Gerätchens immer wieder wundert.
Die gesamte Bauanleitung ist im Internet frei verfügbar und auch das Programm für den Controller kann man kostenlos downloaden.
Inzwischen existieren bereits mehrer Softwareversionen und auch verschiedene Layouts zum Ätzen der Platine, die übrigens nicht größer als das LCD - Display selbst ist.
Die auftretende Frequenzänderung wird von einem Mikroprozessor ausgewertet, dann die Schwingkreisbauteile ausgerechnet und dann die Anzeige auf Null gestellt. Wird nun eine unbekannte Induktivität oder Kapazität eingebracht, so berechnet der Mikroprozessor aufgrund der Frequenzänderung die unbekannte Größe. Das Gerät wurde schon viele Male ohne Probleme nachgebaut und bereitet seinen neuen Besitzern steht's große Freude.
Das LC-Meter nach Phil Rice (VK3BHR) habe ich auch (auf einer Lochrasterplatine) aufgebaut und kann die hervorragenden Eigenschaften nur bestätigen.
Es gibt von Phil jetzt eine verbesserte Variante "Digital LC Meter Version 2" die nur noch mit einem IC 16F628 auskommt und zudem über die Möglichkeit verfügt, per Software kalibriert zu werden. Schaltplan, Leiterplattenlayout und Software unter ironbark.bendigo.latrobe.edu.au/~rice/lc/index2.html bei ebay gibts das Gerät als Fertigmodul für knapp 40 Euro plus Porto. Als Bausatz kostet es noch weniger. Man suche unter "Digital Messgerät LC Meter" Ein Digitalmultimeter mit C - und L - Messung , wenn auch nicht so empfindlich , dafür aber bis 200 μF ( Elkos ) und L = 20 H muss nicht teuer sein .
Zu finden bei www.elv.de unter JT-168 oder Best. Nr. 68-639-88 für € 39,95
ein sehr schönes, kleines, leichtes und exakt arbeitendes Gerät gibt es von LUTRON ELECTRONIC, es heißt LCR - 9063. Unter diesem Namen läßt es sich auch leicht finden.
Hier die Kurzbeschreibung:
http://www.pedak.nl/Lutron/pdf/LCR-9063.pdf Das kleine Gerät ist sehr sparsam, ein 9V Block reicht bei mir nun schon drei Jahre bei fast täglicher Benutzung. Sehr schön ist auch die große Anzeige. Es kostet knapp 40,- Euro. Es kann sogar direkt beim Hersteller http://www.pedak.nl bestellt werden.
Quelle: https://www.radiomuseum.org/forum/l_c_meter_im_eigenbau.html
Das LC-Meter Projekt II Als ich noch nicht Mitglied im RMorg war habe ich ein Projekt "Das LC-Meter Projekt II " realisiert.
Per Google im Internet zu finden.
Einen Link nach extern möchte ich vermeiden.
Die Variante ist, dass man keine Kalibriertaste hat.
Per Software wird jede 2. Messung
der zu messende Bauteil weggeschaltet und so per Mathematik resetted.
Man kann so sofort mit der Messung beginnen.
Es gibt keine Drifterscheinungen, die doch sonst einige pF ausmachen können.
Es gibt auch keinen bekannten Vergleichskondensator, da dieser ja nicht besser ist als der eingebaute Styroflex.
Seit Jahren in Anwendung.
Die Genauigkeit ist beschrieben.
Quelle: https://www.radiomuseum.org/forum/l_c_meter_im_eigenbau.html
********************************************************I*
LCR-Meter
Ein LCR-Messgerät (Induktivität (l), Kapazität (C) und Widerstand (R)) ist ein Instrument zur Messung der Induktivität, Kapazität und des Widerstands einer Komponente, eines Sensors oder eines anderen Geräts, dessen Betrieb von Kapazität, Induktivität oder Widerstand abhängt . IET Labs fertigt eine Vielzahl von LCR-Messgeräten , Kapazitätsmessern und Widerstandsmessern für hohe Widerstandsfähigkeit und Robustheit geringe Widerstandsmessung.
Darüber hinaus stellt IET Labs eine Vielzahl von Widerstands- , Kapazitäts- und Induktivitätsstandards für alle Ihre Kalibrierungsanforderungen her.
Digitale LCR-Meter messen den Strom (I), der durch ein Prüfling fließt (DUT), die Spannung (V) über den Prüfling und den Phasenwinkel zwischen dem gemessenen V und I.
Aus diesen drei Messungen können dann alle Impedanzparameter sein berechnet.
Ein typisches LCR-Messgerät verfügt über vier Kelvin-Anschlüsse zum Anschluss an das zu prüfende Prüfling.
Die Kelvin-Verbindung minimiert Fehler aufgrund von Verkabelung und Verbindung zum Prüfling.
Arten von LCR-Messgeräten Es gibt eine Vielzahl von LCR-Messgeräten vom Handheld bis zum Benchtop. Handheld-DMM mit Kapazitätsmessung sind primär als DMM konzipiert, verwenden jedoch eine DC-Technik zur Kapazitätsmessung.
Die Messung der Kapazität basiert auf der Messung der RC-Zeitkonstante des DUT und der Berechnung der Kapazität. In der Regel haben Zähler dieser Klasse eine Genauigkeit von +/- 1%.
Handheld-LCR- Messgeräte haben den Vorteil, dass sie leicht, tragbar und batteriebetrieben sind.
Die meisten neueren Modelle haben mehrere Testfrequenzen und eine USB-Verbindung für die Übertragung von Daten an einen PC.
Diese sind für allgemeine Anwendungen, insbesondere in Feldwartungs- und Serviceanwendungen, konzipiert.
Dedizierte Handheld-LCR-Messgeräte verwenden ein Wechselstromsignal und bieten in der Regel mehr Impedanzparameter wie AC-Widerstand und Induktivität als ein Handheld-DMM mit Kapazitätsmerkmal.
Die Genauigkeit der Messung liegt in der Regel zwischen 0,2% und 0,1%.
Benchtop LCR- Messgeräte bieten im Allgemeinen mehr Funktionen als Handhelds wie programmierbare Frequenzen,
bessere Messgenauigkeit bis zu 0,01%, Computersteuerung und Datenerfassung für automatisierte Anwendungen.
Fortgeschrittene Merkmale wie DC-Vorspannung und DC-Bias-Strom und Sweep-Fähigkeit sind üblich.
LCR-Messgeräte in dieser Kategorie werden für die AC-Kalibrierung von Induktivitäts-, Kapazitäts- und Widerstandsstandards,
für Messungen der Dielektrizitätskonstante mit einer Vielzahl von dielektrischen Zellen und für die Produktionsprüfung von Komponenten und Sensoren verwendet.
Testfrequenz Elektrische Komponenten müssen mit der Frequenz getestet werden, für die das Endprodukt / die Anwendung verwendet wird.
Ein Instrument mit einem breiten Frequenzbereich und mehreren programmierbaren Frequenzen bietet diese Plattform.
Übliche Messfrequenzen sind 50 / 60Hz, 120Hz, 1kHz, 100kHz und 1MHz.
LCR-Messgeräte mit programmierbaren Frequenzen bieten die größte Flexibilität bei der Anpassung der Frequenz der Messung an die Frequenz,
mit der das DUT tatsächlich verwendet wird oder in F & E-Anwendungen verwendet wird, bei denen die Frequenzcharakterisierung nützlich ist, um einen nützlichen Frequenzbereich oder Resonanz zu bestimmen.
Die meisten LCR-Messgeräte verwenden heute ein AC-Testsignal über einen Frequenzbereich von 10Hz bis 2MHz.
Testspannung Die AC-Ausgangsspannung der meisten LCR-Messgeräte kann so programmiert werden, dass der am DUT anliegende Signalpegel ausgewählt wird.
Im Allgemeinen wird das programmierte Niveau unter einer offenen Schaltungsbedingung erhalten.
Ein Quellenwiderstand (Rs, innerhalb des Zählers) ist effektiv in Reihe mit dem Wechselstromausgang geschaltet, und an diesem Widerstand liegt ein Spannungsabfall vor.
Wenn ein Testgerät angeschlossen wird, hängt die an das Gerät angelegte Spannung vom Wert des Quellwiderstandes (Rs) und vom Impedanzwert des Geräts ab.
Genauigkeit / Geschwindigkeit Klassischer Kompromiss. Je genauer Ihre Messung ist, desto mehr Zeit wird benötigt und umgekehrt, je schneller Ihre Messgeschwindigkeit ist, desto ungenauer ist Ihre Messung.
Aus diesem Grund haben die meisten LCR-Messgeräte drei Messgeschwindigkeiten: langsam, mittel und schnell.
Abhängig von dem zu testenden Gerät haben Sie die Wahl zwischen Genauigkeit und Geschwindigkeit.
Mittelung und Median-Modus können auch helfen, die Messgenauigkeit zu verbessern, aber die Messzeit zu verlängern.
Es ist auch wichtig, in die Genauigkeitsformeln in den Handbüchern zu schauen, da die tatsächliche Genauigkeit der Messung von Frequenz, Spannung und Impedanz des Messobjekts abhängt.
Messparameter Die Primärparameter L, C und R sind nicht die einzigen elektrischen Kriterien zur Charakterisierung einer passiven Komponente und es gibt mehr Informationen in den Sekundärparametern als nur D und Q. Messungen der Leitfähigkeit (G), Suszeptanz (B), Phasenwinkel (q) und ESR kann eine elektrische Komponente, einen Sensor oder ein Material vollständiger definieren. https://de.ietlabs.com/lcr-meter-informational-guide
********************************************************I*
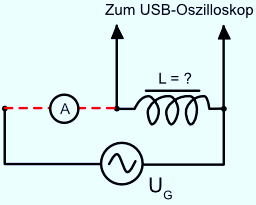
elektor 004035-11 79636-11 Induktivitäten messen 031
Oft muss man sich selbst eine Spule wickeln, oder man findet eine in der Bastelkiste, von der man keine Daten kennt.
Welche Induktivität hat die Spule?
Mit einem Oszilloskop lässt sich das Problem lösen.
Man baut dazu einen Schwingkreis auf und erregt ihn über eine Rechteckquelle (oft am Oszilloskop vorhanden)
und einen kleinen Koppelkondensator zu Eigenschwingungen.
Von Burkhard Kainka
Oft muss man sich selbst eine Spule wickeln, oder man findet eine in der Bastelkiste, von der man keine Daten kennt.
Welche Induktivität hat die Spule?
Mit einem Oszilloskop lässt sich das Problem lösen.
Man baut dazu einen Schwingkreis auf und erregt ihn über eine Rechteckquelle (oft am Oszilloskop vorhanden)
und einen kleinen Koppelkondensator zu Eigenschwingungen.
Nun kann leicht die Resonanzfrequenz f gemessen werden.
Aus f und C = 1000 pF ergibt sich dann die Induktivität:
L = 1 / (4*pi^2 * f^2 * C)
Aber das Oszilloskop kann noch mehr, nämlich die Güte des Kreises bestimmen.
Wenn die Schwingung etwa nach 30 Perioden auf den Faktor I/e=0,37 des Höchstwertes abgefallen ist, ist der Gütefaktor Q = 30.
Die Güte sollte möglichst bei der Frequenz gemessen werden, bei der die Spule auch eingesetzt werden soll.
Man muss also den Schwingkreiskondensator entsprechend wählen.
Der Koppelkondensator 47p muss in jedem Fall sehr viel kleiner sein.
elekor 004035-11
Halbleiterheft Elektor 7-8/2000 Seite 41
https://www.elektormagazine.de/magazine/elektor-200007/962 OHNE LCR-MeterMessen einer Induktivität
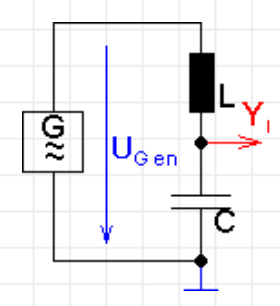
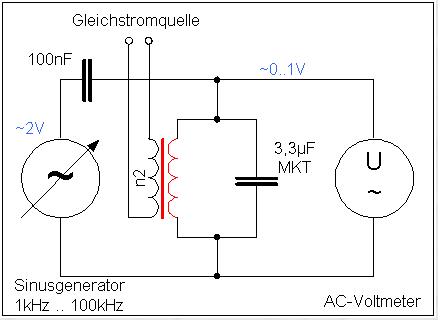
https://www.elektroniktutor.de/analogtechnik/rei_swkr.html
Mit dem Frequenzgenerator stellt man eine feste Spannung UGen ein.
Nun dreht man die Frequenz rauf und runter, bis der Schwingkreis in Resonanz ist.
D.h., die mit dem Oszilloskop gemessene Spannung beträgt die Hälfte von UGen.
Die Induktivität messen - 3 Methoden
Die meisten Multimeter messen alle elektrischen Eigenschaften einer Komponente mit Ausnahme der Induktivität, sodass Sie sich selbst überlassen sind.
Es gibt mehrere Methoden, die wir in diesem Tutorial-Artikel besprechen werden.
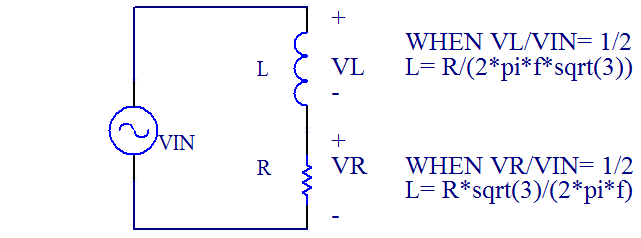
Methode 1 - Induktivität mit Hilfe eines Widerstands messen
Die erste besteht darin, die Induktivität in Reihe mit einem bekannten Widerstand guter Präzision zu schalten, beispielsweise ist ein 100 Ohm 1%-Widerstand eine gute Wahl.
Stimulieren Sie die Schaltung mit einem Funktionsgenerator und betrachten Sie die Verbindung zwischen Widerstand und Induktivität auf dem Oszilloskop sowie die Eingangsspannung.
Stimmen Sie den Funktionsgenerator ab, bis die Sperrschichtspannung die Hälfte der Eingangsspannung beträgt.
Die Beziehung zwischen R und L ist wie unten abgeleitet.
L = unbekannte Spule
R = 100 Ohm +-1% (br-sw-br-br)
Der Vorteil dieser Methode liegt in der Genauigkeit, da Kalibrierwiderstände mit Toleranzen im Bereich von 0,1 % gefunden werden können.
Wenn Sie die Spannung von Spitze zu Spitze am Widerstand messen, verwenden Sie diese Gleichung:
L= R*sqrt(3)/(2*pi*f)
Wenn Sie die Spannung von Spitze zu Spitze am Induktor messen, verwenden Sie diese Gleichung:
L= R/(2*pi*f*sqrt(3))
Ich bevorzuge es, die Spannung am Widerstand statt am Kondensator zu messen, da die Einrichtung einfacher ist,
da Sie Ihre Oszilloskopsonden über den Widerstand legen und dann die Induktivität oder den Kondensator ein- und auswechseln können.
Beachten Sie, dass die Stimulationsfrequenz bei der Messung über den Widerstand 3x höher ist als die des Induktors.
Abhängig vom Frequenzbereich Ihres Geräts und der Eigenresonanz des Induktors kann es vorkommen, dass eine Methode der anderen vorgezogen wird.
Es sollte auch beachtet werden, dass dies für Kondensatoren gilt, die Formel jedoch mit R unten etwas anders ist, wenn über den Widerstand gemessen wird:
C= sqrt(3)/(2*pi*F*R)
Hier ist ein einfacher Rechner:
L= R / (2 * pi * f * sqrt(3) )
Für die Berechnung der Induktivität L brauchst du also den Widerstand (R) und die zuvor bestimmte Frequenz (f).
Die andere Möglichkeit wäre, deine Messwerte in einen Induktivität-Rechner, wie Quelle: https://daycounter.com/Articles/How-To-Measure-Inductance.phtml einzugeben. Multipliziere zuerst den Widerstand mit der Quadratwurzel von 3.
Zum Beispiel:
R = 100R
f = 20 kHz
100 x 1,732 / (2 * 3,141 * 20) =
173 / 125,66 = 1,377 mH (milli-Henry) = 1377uH
Quelle:
https://www.thefastcode.com/de-eur/wiki/Die-Induktivität-messen
https://de.wikihow.com/Die-Induktivität-messen
https://www.daycounter.com/Articles/How-To-Measure-Inductance.phtml
********************************************************I*
Versuch zur Bestimmung der Induktivität einer Spule - Experiment
L = N⋅Φ/I Einheit [L] = Vs/A = H (Henry)
Formel für die Berechnung einer Induktvität L = µ0⋅ µr⋅ A⋅ N² / l L = N² x (µ0*µr*A/l)
D = innen Durchmesser
L = Induktivität N = Anzahl der Windungen µ0 = Magnetische Feldkonstante = 4pi * 10^-7 = 1,2566 x 10 hoch -6 = 0,0000012566 Vs/Am
µ0: magnetische Feldkonstante µ0 = 1,2566⋅10-6 Vs/Am
µr = Permiabilität von Luft 1 + 0,4*10^-6 Permeabilitätszahl 1,0000004 Ohm
µr = Materialkonstante
A: Querschnitt des Spulenkerns
A = Querschnittsfläche der Spule = d2*pi/4 = r2*pi (von einer Windung eingeschlossene Fläche (meistens kreisförmig))
Querschnittsfläche senkrecht zur Spulenachse.
N: Windungszahl
lm: mittlere Feldlinienlänge im Eisenkern l = Länge der Spule Lange Spule l = 1 bis 5x Durchmesser
a) Innendurchmesser d_i verwenden A=di^2∗pi / 4 = 10^2 * 3,14 / 4 = 78,53
Mehrlagige Spulen
b) Mittleren Durchmesser d_m verwenden dm=(da + di) / 2 A=dm^2∗pi / 4 = (20+10/2)^2 * 3,14/4 = 176,71 c) Mittlere Querschnittsfläche verwenden A=(da^2∗pi/4 + di^2∗pi/4) / 2 = (20^2 * 3,14/4 + 10^2 * 3,14/4) / 2 = 196,35
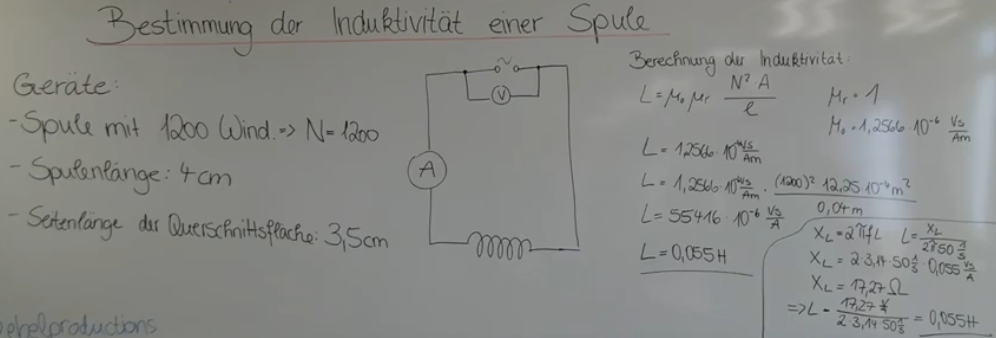
Berechnung:
L = InduktivitätN = 1200 Anzahl der Windungen
l = 4cm = 0,04m Länge der Spule
D = 3,5cm = 0,035m
r = D / 2
µr = Permiabilität von Luft 1 + 0,4*10^-6 Permeabilitätszahl = 1,0000004 Ohm
µ0 = Magnetische Feldkonstante = 4pi * 10^-7 = 1,2566 x 10 hoch -6 = 0,0000012566 Vs/Am (VoltSekunden / AmperMeter)
A = von einer Windung eingeschlossene Fläche (meistens kreisförmig)
A = D^2 = 0,035 * 0,035 = 0,001225m2 = 12,25*10^-4m2
Formel für die kurze Spule L = 0,4..1,5 x D
L = µ0 * µr * N² * A / ( l + 0,9 * r)
Formel für die lange Spule L > D
L = µ0 * µr * N² * A / l = 1,2566*10^-6 * 1 * 1200^2 * 12,25*10^-4 / 0,04 = 5,542*10^-2 = 55,42mH = 0,0554H Vs/A (VoltSekunden/Ampere)
Experiment:
Induktiver Widerstand
L = XL / 2 * pi * f
f = 50 Hz
XL = 2 * pi * f * L = 2 * 3,14 * 50 * 0,0554 = 17,40 Ohm V/A (Volt / Ampere)
Uac = 6,79V
Iac = 0,39A
R = U / A = 6,79 / 0,39 = 17,4 Ohm
Quelle:
https://www.youtube.com/watch?v=zKUFsnmWU88
********************************************************I*
Bestimmung der Induktivität einer Spule mit FG 20kHz~
R = 4,7k Ohm
f = 20 kHz
Mit einem Multimeter wird nun der Spannungsabfall am Widerstand R und an der Spule L gemessen.
In unserem Fall messen wir für
UR=4,44V
UL=2,52V.
Da wir den Wert des Widerstandes kennen, können wir so den Strom bestimmen, der durch diese Serienschaltung und damit auch durch die Spule fließt
I=UR/R = 4,44V / 4,7k = 945uA
Daraus können wir nun den Blindwiderstand XL der Spule bestimmen.
XL = UL / I = 2,52V / 0,945mA = 2,666k Ohm
Nach der Formel
L = XL / (2 * pi * f) = 2666 / (2*3,14*20.000) = 0,0212h = 21,21mH
erhalten wir den Wert für unsere Spule. Bestimmung der Induktivität mittels R-L-C-Serienschwingkreis 
Um den Wert unserer Induktivität bestimmen zu können, benötigen wir den Blindwiderstand XL.
Da die Resonanzbedingung für einen Schwingkreis XL = XC bzw. UL = UC ist, berechnet man den Blindwiderstand des Kondensators mit:  Wir messen die Spannungen am Kondensator und an der Spule und verändern die Frequenz solange, bis beide Spannungen gleich groß sind!
In unserem Fall haben wir UL = UC = 0,282V gemessen.
Hier haben wir Resonanz bei einer Frequenz von fr=925Hz.
Die Werte werden nun in obige Formel eingesetzt.
XC = 78,21 Ohm und damit ist auch (nur bei Resonanz)
XL = 78,21 Ohm Band 1: Gleichstromnetze, Operationsverstärkerschaltungen, elektrische und magnetische FelderDa wir nun unser XL wissen, können wir durch Umwandeln der Formel  L bestimmen. L = 13,5mH
Bestimmen der Induktivität einer Spule durch Wechselspannung schalte die unbekannte Spule mit einem bekannten Kondensator zu einem Parallelschwingkreis.Rege das ganze mit deinem Funktionsgenerator und einen Vorwiderstand an. Such mit dem Oszi die Frequenz, bei der Spannung am Schwingkreis das Maximum erreicht.
Dann rechne aus Frequenz und Kapazität die Induktivität aus (nach Thomson)
Der Widerstand sollte schon etwa genausogross wie der erwartete Blindwiderstand sein.
Ausserdem sollte die Frequenz zu der Arbeitsfrequenz der Spule passen. Bei der Errechnung der Induk- tivität muss man natürlich mit den Phasenwinkeln rechnen.
https://www.youtube.com/watch?v=74fz9iwZ_sM Dafür muss die Kapazität des Kondensators aber wirklich genau bekannt sein. Widerstände haben eine geringere Toleranz.
Das Spannungsverhältnis sollte aber in etwa angeglichen sein um eine höhere Genauigkeit zu erhalten.
Wenn schon mit Widerstand, dann entweder einen kleineren Wert verwenden, oder eine höhere Frequenz benutzen.
1,654V zu 1,49mV ist ein ungünstiges Verhältnis.
Und an die geometrische Addition denken!
Quelle:
https://www.avr-programmierung.com/induktivitaet-einer-spule
Induktivität
Der induktive Blindwiderstand wird von der Frequenz der Wechselspannung und seiner Induktivität beeinflusst.
Der induktive Blindwiderstand ist umso größer, je größer die Induktivität der Spule und je höher die Frequenz der anliegenden Wechselspannung ist.
Das Formelzeichen der Induktivität ist L.
Die Einheit wird zu Ehren des Physikers Joseph Henry mit dem Kurzzeichen H versehen und Henry genannt.
Eine Spule hat die Induktivität 1 Henry, wenn sich die Stromstärke in 1 Sekunde gleichmäßig um 1 Ampere ändert, und dabei eine Spannung von 1 Volt induziert wird.
Mit einem präzisen LCR Meter lässt sich die Induktivität einfach messen.
Quelle:
https://www.lernhelfer.de/schuelerlexikon/physik/artikel/induktiver-widerstand#
https://www.lernhelfer.de/schuelerlexikon/physik/artikel/induktivitaet
https://de.wikipedia.org/wiki/Schwingkreis
********************************************************I*
Bestimmung der Induktivität einer Spule +++ (1A)
Supertester 680R
302_d_ICE-x_I.C.E. Analog-Messinstrument, Supertester Modell 680R (20kOhm-Volt) Anleitung 2_1a.doc Reproduzierbare Messergebnisse erhält man nur mit einem guten Drehspulmessinstrument.Marktübliche digitale Messinstrumente für den Hobbybereich eignen sich bei Wechselstrommessungen unterschiedlicher Frequenzen nicht.
Berechnung der Induktivität
Die Spannung über dem ohmschen Widerstand ergibt sich aus dem Oszillogramm zu Uss = 16,87 V; dies entspricht einem Wert Ueff = 5,96 V. Die Stromstärke in der Reihenschaltung liegt nach Voreinstellung bei Ieff = 25 mA. Der Scheinwiderstand ergibt sich nach (8) zu Z = 238,5 Ohm. Die Induktivität L der Spule errechnet sich dann über (9) mit R = 15,8 Ohm zu L = XL / 2*PI*f = 11,7 mH Der vom Hersteller angegebene Wert für die untersuchte Spule liegt bei L = 10 mH +/- 10%.
Eine Kontrollmessung mit einem digitalen Meßgerät ergibt einen Wert von 8,4 mH.
Quelle:
https://www.rahner-edu.de/grundlagen/signale-richtig-verstehen/rl-schaltung-2/
https://xplainme.com/44983-bestimmung-der-induktivitat
https://www.youtube.com/watch?v=zKUFsnmWU88
https://www.youtube.com/watch?v=w49Ops7rffo
https://www.youtube.com/watch?v=_ziQZkBUTKw
https://de.wikipedia.org/wiki/Induktivität
********************************************************I*
Messungen anInduktivitätenund Kondensatoren (1A)
MessungderSpulenparameterSpulen gehören zu den wenigenBauteilen,die man immer noch selbst anfertigen kann.
Aber auch wenn man siekauft,weiß man nicht wirklich alles über die Spule.
Für denBetriebder Spule in einem Schaltregler sind vor allem drei Parameter vonBedeutung
BestimmungdesSpuleninnenwiderstandes
R = 0,178 * L / A = 0,227* L/ d2 [in Milliohm]
BestimmungderSpuleninduktivität
AL = L / N2
BestimmungderKernsättigung/
Quelle:
http://www.sprut.de/electronic/switch/lc/lc.html
********************************************************I*
Methoden zur Messung der Induktivität mit hoher Präzision
Quelle:
https://meettechniek.info/passive/inductance.html
https://qastack.com.de/electronics/417354/methods-to-measure-inductance-with-high-1-precision-using-standard-equipment
********************************************************I*
Was ist der beste / einfachste Weg, um eine unbekannte Induktivität ohne RLC-Messgerät zu messen?
Gibt es eine gute Möglichkeit, die Induktivität mit einem Oszilloskop und einem Funktionsgenerator genau zu messen?
Die beste Methode, die ich finden kann, besteht darin, einen Tankkreis aufzubauen und die Frequenz zu überstreichen, bis die höchste Spannung auftritt.
Verwenden Sie dann die folgende Formel, um zu lösen:
Es scheint einen einfacheren Weg zu geben!
Ich habe einen Oszillator mit zwei Anschlüssen verwendet, bei dem der Induktor parallel zu einem geeigneten Kondensator ist,
mit einem Oszilloskop oder Zähler, um die Schwingungsfrequenz zu messen.
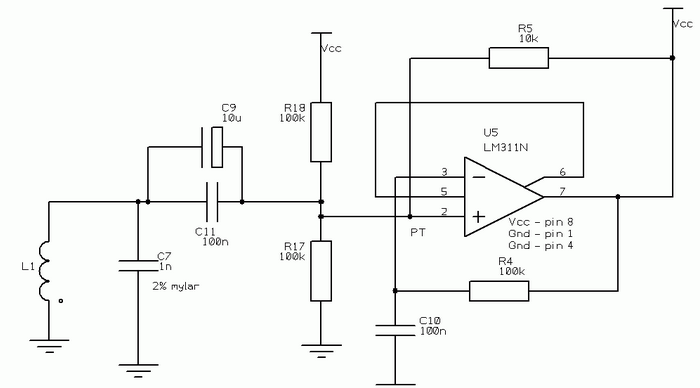
Ich habe einmal einen Induktor an einem sehr teuren Induktivitätsmesser bei der Arbeit überprüft, und die Werte waren identisch. Der quellengekoppelte Oszillator mit zwei FETs ist ideal für diese Anwendung oder den LM311:
Die Sweep- und Oszillator-Methoden sind beide anständige Methoden, aber Sie müssen in vielen Fällen den Wert der parasitären Eigenkapazität des Induktors berücksichtigen.
Sie sollten auch überlegen, welche Fehler auftreten können, wenn das Q des abgestimmten Schaltkreises niedrig ist.
Mehr dazu unten, aber im Moment gehe ich davon aus, dass Sie einen Resonanzkreis mit hohem Q aus einem unbekannten L und einem bekannten C erstellen können.
Quelle:
https://qastack.com.de/electronics/61858/whats-the-best-easiest-way-to-measure-an-unkown-inductance-without-an-rlc-meter
Induktivität mit dem Oszilloskop messen
Für den Bau einer Speicherdrossel mit ca. 470 µH habe ich keinen kleinen Ringkern (ausgebaut aus einer Energiesparlampe) bewickelt.
Bei einem unbekannten Kern weiß man nie, welche Induktivität dabei herauskommt.
Deshalb kam wieder eine bewährte Messmethode mit dem Oszilloskop zum Einsatz:
Ich löte einen bekannten Kondensator an die Spule und verbinde den Parallelschwingkreis mit dem Oszilloskop.
Das heiße Ende wird dann nahe an den 1 kHz Rechteckausgang des Oszis gelegt oder ich benutze einen sehr kleinen Koppelkondensator (< 100 pF).
Dabei entstehen freie Schwingungen auf der Resonanzfrequenz.
Mit dem Oszi lässt sich die Frequenz ausreichend genau durch Abzählen von Schwingungen bestimmen.
In diesem Fall konnte die Resonanzfrequenz mit 360 kHz gemessen werden.
Nun kommt mein Programm LCFR zum Einsatz.
Ich tippe die Kapazität 330 pF ein und probiere so lange an der Induktivität herum, bis die Frequenz stimmt.
Drei bis vier Versuche reichen, dann steht das Ergebnis fest: 580 µH.
Das liegt ausreichend nahe an dem gewünschten Wert von 470 µH.
Glück gehabt!
Man könnte es natürlich auch einfach ausrechnen.
Quelle:
https://www.elektronik-labor.de/Elo/OsziL.html
http://www.b-kainka.de/bastel95.htm
********************************************************I*
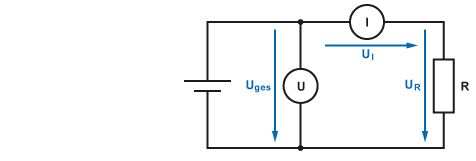
Induktivitäten messen Ich machs mit dieser Methode:
1. Spule mit Vorwiderstand an Wechselspannung (z.B. 1kHz) anlegen (RL in Serie)
2. Mit Oszi den Strom messen
3. Aus dem Strom die Impedanz berechnen
Z=U/I
4. Aus der Impedanz und dem Widerstand R, XL berechnen:
Z=√ R^2+XL^2 = Wurzel aus R Quadrat + XL Quadrat
5. Mit der Formel für XL, L berechnen:
XL=2⋅π⋅f⋅L
Spule
Die Spule speichert magnetische Energie.
Die wichtigste Kenngröße der Spule ist die Induktivität.
Die Induktivität ist ein Maß für die Speicherfähigkeit von magnetischer Energie. Die Induktivität wird als Verhältnis des gesamten magnetischen Flusses NΦ zur Stromstärke I definiert: L = N⋅Φ/I Einheit [L] = Vs/A = H (Henry) Formel für die Berechnung einer Induktvität L = µ0⋅ µr⋅ A⋅ N2/lm
µ0: magnetische Feldkonstante µ0 =1,257⋅10-6 Vs/Am.
Berechnung der Induktivität einer Spule
Wenn sich die Anzahl der Windungen N verdoppelt, vervierfacht sich die Induktivität L.
Magnetische Energie einer Spule Wmagn = 0,5⋅L⋅I2 Berechnung der gespeicherten EnergieDer Zusammenhang zwischen Stromstärke und Spannung: Das InduktionsgesetzWenn sich die Stromstärke in einer Spule ändert, dann wird in der Spule eine Spannung erzeugt (induziert).
Die Spannung kann mit dem Oszilloskop gemessen werden.
u(t) = L⋅Δi/Δt Berechnung des induktiven Spannungsfalls Je kleiner die Zeitänderung (Zeitdifferenz) Δt, desto größer die induzierte Spannung
Quelle:
http://home.teleos-web.de/vsteinkamp/get/spule/spule.htm
********************************************************I*
Induktivität von Spulen ermitteln
beim ausmessen von Spulen für mein Audion ist mir aufgefallen, dass mein L-Messgerät ein Problem hat.
Bei einer Spule, die 470uH haben sollte, zeigt mir mein Gerät 505uH an.
Ich kann mir nicht vorstellen, dass die Spule so weit abweichen sollte.
Aus diesem Grund habe ich mir mal eine kleine Messschaltung aufgebaut.
Eine Spule wird ja in einem Schwingkreis ermittelt, also habe ich die Spule über eine sehr niedrige Kapazität an meinen Oszillator angekoppelt.
Mit dem Oszi habe ich jetzt nach der obersten Resonanzfrequenz (grösste Amplitude) gesucht.
Um die Eingangskapazität meiner Prüfspitze weitgehenst auszuschliessen habe ich noch einmal über einen 3,3pF Kondensator gemessen.
Wie erwartet lag die Resonanzfrequenz natürlich daneben.
Die 12,5pF (lt. meiner Messung 16,8pF) machen sich doch stark bemerkbar.
Ein Problem habe ich aber immer noch.
Wie ermittelt man (oder mein L-Meter) die 'echte' Induktivität, da man ja nicht die parasitäre Kapazität kennt?
Wenn man annimmt, dass die Angabe des Herstellers der Spule stimmt, dann kann man die Kapazität über die Resonanzfrequenz ermitteln,
aber wenn die Induktivität und Kapazität abweicht, dann hat man auch die gleiche Resonanzfrequenz.
Kann mir vielleicht hier jemand von Euch weiterhelfen, denn Ich stehe voll auf dem Schlauch. Ein Problem habe ich aber immer noch.
Wie ermittelt man (oder mein L-Meter) die 'echte' Induktivität, da man ja nicht die parasitäre Kapazität kennt?
Norbert Hallo Norbert, wenn ich Dich richtig verstehe, möchtest Du folgendes wissen: eine reale Spule ist immer ein Gebilde mit einer Induktivität, einer Eigenkapazität und einem Ohmschen Widerstand. Wenn man den ohmschen Widerstand mal vernachlässigt bzw. dieser 'sehr' klein ist, kann man die Spule als einen Schwingkreis
mit einer Eigenresonanz auffassen, die sich aus Eigeninduktivität und Eigenkapazität ergibt.
Wie groß ist die Eigeninduktivität bzw. die Eigenkapazität?
Ich könnte Dir so auf die Schnelle zwei Methoden vorschlagen, das herauszufinden . . . Die erste ist die algebraische Methode: Du mißt einmal die Resonanzfrequenz Deiner Spule mit Deiner Meßanordnung wie gehabt. Dann schaltest Du einen bekannten Kondensator parallel zur Spule (z.B. das 10fache der vermuteten Eigenkapazität)
und mißt die Resonzfrequenz mit der gleichen Meßanordnung nochmal.
Jetzt hast Du zwei Gleichungen, Thomsonsche Schwingungsgleichungen, für Deine beiden Unbekannten, Eigeninduktivität und Eigenkapazität.
Der Rest ist einfache Algebra.
W1^2 = 1/(L*C1) und W2^2 = 1/(L*(C1+C2)) wobei W1 und W2 = Kreisfrequenz bei Resonanz = 2*pi*f1 bzw. 2*pi*f2 f1 = Resonanzfrequenz ohne ZusatzKondensator nur mit (Eigenkapazität + SchaltKapazität) C1 f2 = Resonanzfrequenz mit ZusatzKondensator C2 L = Eigeninduktivität der Spule Unbekannt sind L und C1. Gemessen werden W1 und W2 und C2. Voraussetzung ist wie oben angenommen, daß der ohmsche Widerstand der Spule gering ist.
Die Thomsonsche Schwingungsformel gilt exakt nur für verlustlose Spulen.
Die andere Methode ist die graphische Methode. Du machst mehrere Messungen wie oben aber mit mehreren unterschiedlichen aber bekannten ZusatzKondensatoren. Dann trägst Du auf Millimeterpapier auf der X-Achse (Abszisse) die jeweilige Zusatzkapazität ein
und darüber in Richtung Y-Achse (Ordinate) den jeweils dazugehörigen gemessenen Wert von 1/W^2.
Wenn alles richtig läuft, kannst Du eine Gerade durch alle Meßpunkte legen.
Die Steigung der Geraden ist die gesuchte Induktivität. (Werte natürlich im MKS-System, also in V, A und sec einsetzen.)
Dort wo die Gerade die Ordinate schneidet kannst Du die Eigenresonanz Deiner Spule ablesen (bzw. aus dem Ordinatenwert berechnen). Statt Millimeterpapier kann man natürlich auch Excel o.ä. nehmen. Hallo Norbert Eine Frage ist, mit welcher tatsächlichen Genauigkeit dein L-Messgerät bei solch relativ kleinen Induktivitätswerten messen kann? Der andere Punkt ist, ob sich sich im Laufe der Zeit an dieser Spule nicht irgend etwas verändert hat. Ich habe mir ein R-L-C-Messgerät beim blauen C gekauft.
Das misst leider in den kleineren für uns interessanten Messgrößen der Schwingkreistechnik relativ ungenau.
Für genauere Messungen habe ich mir für ca. 30 € einen Selbstbausatz gekauft, der die kleinen Bereiche der Induktivität und Kapazität mit guter Genauigkeit misst.
Das Multimeter ist eben nur als R-Messer und ansonsten für die größeren Maßeinheiten tauglich.
Freundliche Grüße von Dietmar die Berechnung ist mir ja klar, nur habe ich zwei Unbekannte. Mal als Beispiel, ich habe hier eine Spule die bei 984,3kHz in Resonanz ist. L und C sind unbekannt.
Jetzt schalte ich einen 3,3pF Kondensator parallel zur Spule, wodurch die Resonanz jetzt bei 919,1kHz liegt.
Trotzdem komme ich aber immer noch nicht auf die Werte der Spule.
Zugegeben, ich habe hier eben gerade etwas geschummelt, denn ich kenne den auf der Spule angegebenen Wert (1mH).
Wenn er stimmen sollte, dann müsste die parallele Kapazität 26,145pF sein. Wie erkennt aber das Messgerät den Wert?
Übrigens, bei C=29,445pF und L=887,92uH komme ich auch auf eine Resonanzfrequenz von 984,3kHz. Die einzige Möglichkeit, die mir eingefallen ist, das ist eine zusätzliche Strommessung.
Da im Resonanzfall ja Xl=Xc ist, kennt man somit den Blindwiderstand und mit der Formel L=Xl/2*Pi*f lässt sich dann die Induktivität (bzw. Kapazität) errechnen.
Wenn ich mal vieeeeeel Zeit habe, dann werde ich mir mal eine kleine Schaltung zur Messung des Stroms aufbauen.
Bis dahin werde ich mich aber weiterhin auf mein LCR-Messgerät verlassen müssen.
Dietmar Ich glaube, ich habe das gleiche Gerätchen (LCR4080) wie Du.
Die Kapazitäten misst es eigentlich recht gut. Man muss vorher nur immer kalibrieren.
Gruss Norbert Hallo Heinz, Mal als Beispiel, ich habe hier eine Spule die bei 984,3kHz in Resonanz ist. L und C sind unbekannt.
Jetzt schalte ich einen 3,3pF Kondensator parallel zur Spule, wodurch die Resonanz jetzt bei 919,1kHz liegt.
Trotzdem komme ich aber immer noch nicht auf die Werte der Spule.
leichtsinnigerweise habe ich angenommen, daß die Sache mit den zwei Gleichungen und den zwei Unbekannten jedem mitlesenden hier ohne weiteres geläufig ist.
In einem früheren Leben war das für mich tägliches Brot.
Deshalb erliege ich immer wieder der irrigen Annahme, daß das für alle anderen genauso ist.
Hier also der Rechengang noch einmal ausführlicher und in Schönschrift: Der 'Fehler' von ca. 16% bei der Induktivität dürfte sich im wesentlichen daraus ergeben, daß ich angenommen habe,
daß der Kapazitätswert von 3.3pF exakt stimmt (immer vorausgesetzt, daß auch die Angabe: 1mH exakt stimmt).
Tatsächlich haben kleine Keramikkondensatoren in dieser Kapazitätsgröße eher Toleranzen bis zu +/- 30...40%.
Da kann das Endergebnis Induktivität natürlich nicht genauer sein.
Bei der graphischen Methode, wo man mehr Messungen macht und über diese mittelt - dadurch, daß man eine Ausgleichsgerade zieht - wird der Fehler noch geringer. Wie erkennt aber das Messgerät den Wert? Ich denke mal, daß Du kein Meßgerät finden wirst, das die Kapazität richtig erkennt, wenn dieser Kapazität ein etwa gleichgroßer induktiver Scheinwiderstand parallel liegt. In solchen Fällen wird man wohl auf andere Meßmethoden zurückgreifen müssen.
So wie die hier vorgeschlagene.
Auch die von Dir angedachte Strom-Messung liefert eine zweite Gleichung zur Bestimmung der beiden Unbekannten. Hallo Norbert, man muss wohl mit zwei unterschiedlichen Messfrequenzen und auch Kondensatoren messen.
Dann ergibt sich folgende Rechnung:
http://www. radiomuseum.org/forum/eigenkapazitaet_von_spulen.html (Leerzeichen eingefügt) Bei meiner Messbrücke soll das auch so funktionieren. .... http://www.wumpus-gollum-forum.de/forum/...r-3-54_122.html erzählte mir der Vorbesitzer.
Ich glaube das macht wirklich Sinn.
Bei meinem Gerät wird die Frequenz verdoppelt um
C_eigen zu bestimmen. Auf dem Bild in meinem Beitrag ist eine aufgeklebte handschriftliche Notiz mit dem Ablauf sichtbar. Ich bin noch nicht dazu gekommen mit dem Oszi nachzumessen.
Ich kannte dieses Prinzip auch noch nicht. Im Link siehst Du einen
Techniker der alten Schule..nur mit Papier und Bleistift ausgerüstet. Heinz hat dieses Prinzip in seinen Berechnungen ja auch schon aufgezeigt.
Bei meiner Messbrücke kann ich die Eigenkapazität direkt am linken Messwerk in pF ablesen und muss nicht rechnen.
Das ist natürlich eine feine Sache. Bekannte Referenzspulen brachten exakt das Ergebnis.
Zitat zum Messaufbau von Hr. Birkner: " - Arbeitet man mit ausreichend großen Entkopplungswiderständen, dann entfällt der Einfluss der Messköpfe.
Allerdings bildet das einen RC-Tiefpass. der einen starken Amplitudenverlust am Messkopf verursacht und entsprechend hohe Anzeigeempfindlichkeit verlangt.
Man kann sich da auch mit einen HF-Millivoltmeter oder einem geeigneten Empfänger behelfen.
- Man kann aber auch die Eingangskapazität des Messkopfes ermitteln.
Gute 1:10 Messköpfe zeigen dabei nach meiner Erfahrung sehr genau 10 pF bei exaktem (!) Abgleich.
"
Zitat Ende.
Hallo Norbert und zusammen, bei mir läuft es einwandfrei. Zusammen mit Deiner einfachen Testschaltung dürfte es wohl eine der billigsten Methoden sein, Induktivität und Eigenkapazität einer Spule zu ermitteln. Die hier von 'Joe' verlinkten Methoden arbeiten im wesentlichen nach dem gleichen Prinzip soweit ich das mit einem flüchtigen ersten Blick erkennen konnte.
Mein Vorschlag bezog sich aber speziell auf die oben im Thread dargestellte Testschaltung.
Das Prinzip aller dieser Messungen, wie sie auch im Radiomuseum-Forum zitiert werden, ist übrigens nicht auf die Ermittlung von Eigenkapazitäten beschränkt.
Es geht zurück auf das mathematische Problem, zwei Unbekannte zu ermitteln aus zwei Gleichungen, die diese Unbekannten enthalten.
Dieses Prinzip wird in den Naturwissenschaften seit 'ewigen' Zeiten, also schon vor der Erfindung der Elektronk, bei vielen verschiedenen Meßproblemen benutzt.
Zur Bestimmung der beiden Unbekannten sind also schon aus mathematischen Gründen immer (mindestens) zwei Messungen notwendig.
Wie man diese durchführt ist dann dem eigenen Ermessen überlassen. Auch für die mathematische Auswertung dieser Messungen sind natürlich verschiedene Wege denkbar.
Mit moderner Digitaltechnik wäre es wohl realisierbar, beide Messungen mit einem Knopfdruck durchzuführen.
Es werden im Prinzip aber immer zwei Messungen benötigt.
Möglicherweise unterscheiden sich die verschiedenen Methoden in ihrer Genauigkeit etwas.
Der Ingenieur würde hier eine Fehleranalyse durchführen (heute nennt man das 'Sensitivitäts-Studie') und sich dann für die einfachste Methode entscheiden, die seinen Anforderungen genügt.
Als Bastler strebt man meist eine Methode an, die den geringsten Aufwand verursacht.
Auch hier lohnt es sich aber, mal über die erreichbare Genauigkeit nachzudenken.
Gruß Heinz
Quelle:
https://www.wumpus-gollum-forum.de/forum/thread.php?board=54&thread=126
********************************************************I* Arduino Induktivität / Kapazität / WiderstandsmessgerätARDUINO UNO mit ATmega328P Arduino-UNO-R3-based-LC-meter LM741 LM393 Regulatorischen L7805CV LCD 16 X 2 X = 16MHz Crystal Kondensatoren: 0.33uF 100nF 2x 22pF Polyester 1uF Widerstände: 10k Potentiometer 7x 10k 2x 220 Ohm 1M 150 Ohm 330 Ohm Dioden: 1N4004 Anschlüsse: Block 2-Klemme 4x MOLEX 100 verbrachte 2-pin 4-Pin MOLEX 100 ausgegeben 4x Borne 2x Schalter 2x Taster
Chasis
Quelle:
https://www.genstr.com/arduino-induktivitat-kapazitat-widerstandsmessgerat.htmlhttps://github.com/alpop/Arduino-UNO-R3-based-LC-meter https://github.com/alpop/Arduino-UNO-R3-based-LC-meter/blob/master/LC_meter.ino
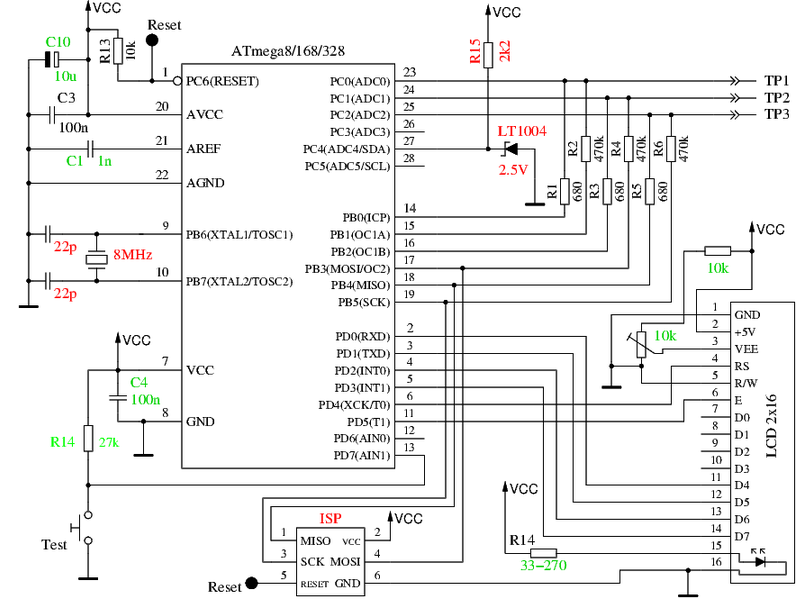
ARDUINO LCR Meter ArduTester V1.13 ArduTester V1.13: The Arduino UNO Transistor TesterArdutester - Arduino Component Tester TransistorTester mit AVR-Mikrocontroller STAND 22.03.2021
Ein Gerät zur Bestimmung und Messung von elektronischen Bauteilen und ein wenig mehr . . . Karl-Heinz KübbelerVersion 1.13k [email protected] ArduTester Fritzing schematics Schaltplan ardutester_v113_otPu7eBf45.fzz Downloads (deutsch) Die aktuelle Version von Software und Dokumentation ist nun auf GitHub.com/Mikrocontroller-net/transistortester abrufbar. Die Doku ist auf deutsch und englisch und russisch und tschechisch verfügbar. Die Benutzer können mit dem Kommando "git clone https://github.com/Mikrocontroller-net/transistortester" eine vollständige Kopie des Archivs in ein neu erstelltes transistortester Verzeichnis herunterladen. Im Arbeitsverzeichnis transistortester kann man mit "git checkout" die Kopie auf den letzten Stand bringen. Messung eines bipolaren PNP Transistors
Quelle:
300_d_Kübbeler-x_TransistorTester mit AVR-Mikrocontroller (2021) - Bauanleitung (149 Seiten)_1a.pdf https://create.arduino.cc/projecthub/plouc68000/ardutester-v1-13-the-arduino-uno-transistor-tester-dbafb4
https://www.mikrocontroller.net/articles/AVR_Transistortester#Downloads_.28English.29
https://github.com/svn2github/transistortester?ref=https://githubhelp.com
[1] Markus Frejek AVR-Transistortester,. Embedded Projects Journal, 11. Ausgabe, 2011 [2] https://github.com/mikrocontroller-net/transistortester/blob/master/Doku/trunk/pdftex/german/ttester.pdf [3] Atmel Corporation 8-bit AVR with 8KBytes In-System Programmable Flash - ATmega8(L),.Manual, 2486Z-AVR-02/11, 2011 [4] Atmel Corporation 8-bit AVR with 4/8/16/32KBytes In-System Programmable Flash - ATmega48- ATmega328,. Manual, 8271D-AVR-05/11, 2011 [5] Atmel Corporation Atmel AVR126: ADC of megaAVR in Single Ended Mode,. Application Note,8444A-AVR-10/11, 2011 [6] Atmel Corporation Atmel AVR121: Enhancing ADC resolution by oversampling,. ApplicationNote, 8003A-AVR-09/05, 2005 [7] http://en.wikibooks.org/wiki/LaTeX LaTeX documentation,. Guide to the LaTeX markuplanguage, 2012 [8] http://en.wikibooks.org/wiki/Gnuplot Gnuplot documentation,. Documentation for theplotting tool gnuplot, 2012 [9] Wikipedia http://de.wikipedia.org/wiki/Equivalent_Series_Resistance Erläuterungzum ESR. Normung und Ersatzschaltbild eines Kondensators, 2012 [10] http://www.xfig.org/userman Xfig documentation,. Documentation of the interactive drawingtool xfig, 2009 [11] http://docs.gimp.org/2.6/de gimp documentation. Documentation of the GNU Image Mani-polation Program, 2010 [12] http://www.mikrocontroller.net/articles/AVR-Transistortester Online Dokumentationdes Transistortester, Online Article, 2009-2011 [13] http://www.mikrocontroller.net/articles/AVRDUDE Online Dokumentation des avrdudeprogrammer interface, Online Article, 2004-2011 [14] http://www.mikrocontroller.net/topic/131804 Thread von Markus F., Forum thread, 2009 [15] http://www.mikrocontroller.net/articles/AVR_Transistortester Kurze Eigenschaftenbeschreibung des TransistorTester von Karl-Heinz K., Online Article, 2012 [16] http://www.mikrocontroller.net/topic/248078 Thread von Karl-Heinz K., Thread und Software Versionen, 2012 [17] http://www.mikrocontroller.net/articles/WinAVR Artikel über WinAVR, Online Artikel, 2012 [18] http://sourceforge.net/projects/winavr/files Quelle für WinAVR, Download Quelle, 2012 [19] http://www.mikrocontroller.net/topic/248078?page=5#2922341 Patch für WinAVR, Setzen der Fuses mit avrdude, Download Quelle, 2012 [20] http://www.orientdisplay.com/pdf/ST7565.pdf Datenblatt des grafischen Controllers ST7565, Download Quelle, 2014 [21] Maxim Integrated Products, Inc. http://maximintegrated.com DS3231: Extremely Accurate I2C-Integrated RTC/TCXO/Crystal, Data Sheet, 19-5170;Rev 10; 3/15, 2015 [22] Maxim Integrated Products, Inc. http://maximintegrated.com DS3231M: 5ppm I2C Real-Time Clock, Data Sheet, 19-5312;Rev 7; 3/15, 2015
********************************************************I*
Ein Meßgerät für Induktivitäten und Kapazitäten mit einem Atmel ATMega163 Microcontroller (LC-Meter)
Anforderungen
1) Das LC-Meßgerät muß sowohl sehr kleine Induktivitäten (kleiner 1 μH) als auch sehr große Induktivitäten (nicht unter 100 mH) messen können. 2) Das LC-Meßgerät muß in der Lage sein, Kapazitäten aufgrund des Layouts und des Oszillators zu ermitteln und bei der Berechung der Induktivität zu berücksichtigen.
Diese Forderung ist gleichbedeutend mit dem Wunsch, auch unbekannte Kapazitäten messen zu können.
3) Eine zum vorigen Punkt verwandte Forderung ist, daß eine Induktivität bereits einen Kondensator parallel geschaltet haben darf, der die L-Messung nicht beeinträchtigt. 4) Idealerweise sollte die Induktivitätsmessung direkt oder indirekt auf eine Widerstandsmessung zurückgeführt werden.
Grund ist vor allem, daß man nicht an jeder Straßenecke Induktivitäten mit geringer Toleranz und hoher Langzeitstabilität beschaffen kann.
Bei Kondensatoren ist die Situation schon besser - Kondensatoren mit 2,5% Toleranz sind durchaus im einschlägigen Versandhandel erhältlich.
Noch geringere Toleranzen sind bei Widerständen möglich - vor allem, wenn sie für Meßzwecke ausgelegt wurden (0,1%).
Quelle:
https://www.dl8nci.de/lc-meter-001.html
********************************************************I*
LC-Meter Bausatz mit PIC16F628A - Accurate LC Meter Kit
Voltage Supply: 6 - 16V Accuracy: 1% Full Automatic Ranging Inductance Resolution: 10nH Capacitance Resolution: 0.1pF LC Meter's Inductance Measurement Ranges: - 10nH - 1000nH - 1uH - 1000uH - 1mH - 100mH LC Meter's Capacitance Measurement Ranges: - 0.1pF - 1000pF - 1nF - 900nF
1x 16x2 LCD Display with Green / Blue Backlight
1x PIC16F628A Programmed Microcontroller 1x LM311 IC 1x Accurate LC Meter PCB with red solder mask 1x Enclosure 1x Gold Plated Machined 18 DIP IC Socket 1x Gold Plated Machined 8 DIP IC Socket 1x L/C Pushbutton Switch with Black Cap 1x Tactile momentary reset switch with Black Cap 1x Gold Plated 16-PIN LCD Female Header 1x Gold Plated 16-PIN LCD Male Header 1x Gold Plated 2-PIN Header 2x Gold Plated 1-PIN Header 1x 4.000 MHz Crystal 1x High Precision 82uH Inductor 1x 5V Ceramic Reed Relay 1x LM7805 Regulator 1x 10K LCD Contrast Trimmer 2x 1000pF High Precision WIMA Capacitor 1x 100nF High Quality WIMA Capacitor 2x 10pF High Stability Capacitor 2x 10uF Panasonic Capacitor 1x 33 1% Metal Film Resistor 1x 100 1% Metal Film Resistor 1x 1K 1% Metal Film Resistor 2x 6.8K 1% Metal Film Resistor 1x 47K 1% Metal Film Resistor 3x 100K 1% Metal Film Resistor
Quelle:
http://electronics-diy.com/lc_meter.php
********************************************************I*
Vorsicht:
Entladung vor der Kapazitätmessung !!
Mit Funktionsgenerator und Echt-Effektiv-Wert-Messung Multimeter (TrueRMS).
Kapazität bestimmen
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| U in Volt | I in mA |
R in Ω (berechnet) Stromfehlerschaltung |
R in Ω (berechnet) Spannungsfehlerschaltung |
|---|---|---|---|
| 20 | 90 | 222 | 222 |
| 0,2 | 0,91 | 220 | 333 |
Typischerweise ist der Innenwiderstand von Spannungsmessern sehr groß.
Die Stromfehlerschaltung eignet sich deshalb nur zur Widerstandsmessung an kleinen Widerständen,
Sobald man mit dieser Schaltung an einem großen Widerstand messen will, verfälscht die Parallelschaltung
Spannungsfehlerschaltung (Spannungsmesser vor Strommesser)
Bei der Spannungsfehlerschaltung entsteht ein Spannungsteiler aus dem Innenwiderstand des Strommessgerätes und dem zu messenden Widerstand.
Der Spannungsabfall Ui am Strommessgerät verfälscht die Spannungsmessung.
Die gemessene Spannung Uges ist um die Spannung Ui zu groß.
Messung mit R = 10 kΩ
| U in Volt | I in mA |
R in Ω (berechnet) Stromfehlerschaltung |
R in Ω (berechnet) Spannungsfehlerschaltung |
|---|---|---|---|
| 20 | 2,4 | 8333 | 10000 |
| 0,2 | 0,024 | 8333 | 10000 |
Typischerweise ist der Innenwiderstand von Strommessern sehr klein.
Die Spannungsfehlerschaltung eignet sich deshalb nur für Messungen an großen Widerständen, wo der Spannungsabfall am Innenwiderstand des Strommessers die Messung sehr wenig beeinflusst.
Sobald man mit dieser Schaltung einen kleinen Widerstand messen will, verfälscht die Reihenschaltung aus Innenwiderstand des Strommessers und dem zu messenden Widerstand das Ergebnis.
Elektronische Multimeter sind bei der Spannungsmessung sehr hochohmig (1,0..10M Ohm).
Daher hat die Stromfehlerschaltung nur dann eine Bedeutung wenn sehr kleine Ströme (µA-Bereich) gemessen werden.
Die Spannungsfehlerschaltung kommt aber ebenso zur Anwendung, weil der Shunt-Widerstand im Messgerät einen relevanten Spannungsabfall bewirkt.
Quelle:
http://www.elektronik-kompendium.de/sites/grd/0306091.htm
Weitere verwandte Themen:
DIN A4 ausdrucken
ENDE