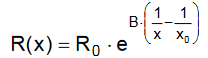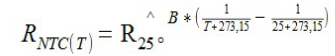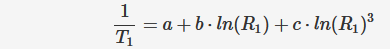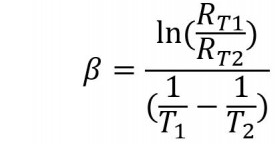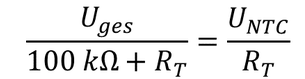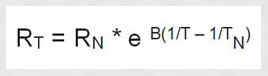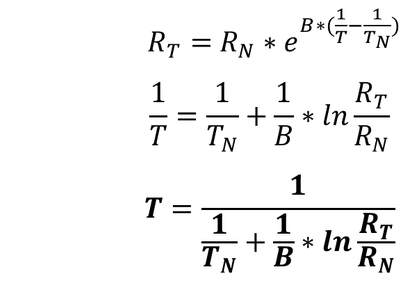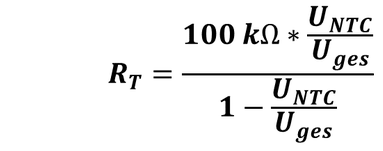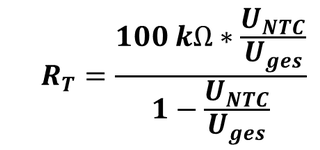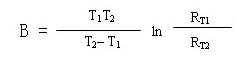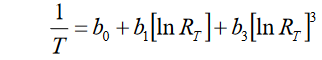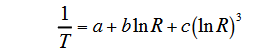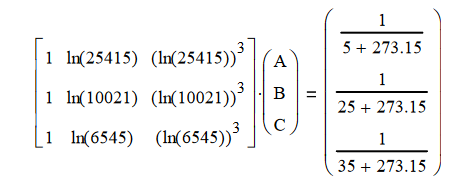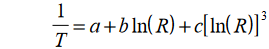|
http://sites.schaltungen.at/elektronik/ntc-ptc
Wels, am 2021-11-20BITTE nützen Sie doch rechts OBEN das Suchfeld [ ] [ Diese Site durchsuchen]DIN A3 oder DIN A4 quer ausdrucken
*******************************************************************************I** DIN A4 ausdrucken (Heftrand 15mm / 5mm) siehe http://sites.schaltungen.at/drucker/sites-prenninger
********************************************************I* 015_b_PrennIng-a_elektronik-ntc.ptc (400 Seiten)_1a.pdf
Untergeordnete Seiten (1):
Temperaturen messen ist möglich mit
1) Thermoelemente Typ K 41uV/°C bis 1.200°C es wird eine Vergleichsstelle benötigt z.B. AD84942) Widerstandsthermometer (RTD-Sensoren) PT100 (100 Ohm bei 0°C) bis 500°C präziser Treiberstrom notwendig (Vierleiter-Schaltung) 3) Thermistoren NTC-PTC kostengünstig aber nichtliniares Verhalten (Steinhart-Hart-Gleichung) kalibrieren mit LTC2986 4) Transistor-Temperatursensoren temperaturabhängigkeit der B-E Spannung mit 2N2222
492_b_Vordruck-OH_VHS2.3.27 Temperaturabhängigkeit eines Transistors_1a.pdf
493_b_Text-x_VHS3.2.38 Op-Amp als Temperatur-Fernkontrolle, mit Transistor als Sensor_1a.pdf
493_b_Text-x_VHS3.2.40 Op-Amp als Temperatur-Meßgerät (Transistor als Sensor)_1a.pdf
Temperaturmessung mit mini Transistoren Verwenden sollte man die Basis-Emitter-Diode (B-C kurschluss) eines Niederfrequenztransistors mit hoher Stromverstärkung (z.B. 2N2907).mini NF Transistor als Temperatursensor (B-C kurschluss)
http://www.michael-muth.de/lectures/TempSens/chap05.html
5) Halbleiter-Temperatursensoren ADT7422 +/-0,1°C ADT7320 Messgenauigkeit +/-0,2°C für Fieberthermometer
ADT7422 +/- 0,8°C
Analoge-Sensoren: AD592 KTY81 LM135 LM235 LM335
Digitale-Sensoren: DS1820 DS18S20 TSic-206 TSic 306 TSic-506 AD7314
https://de.wikipedia.org/wiki/Halbleiter-Temperatursensor
6) IR-Temperatursensoren / Thermosäulen / Infrarot-Sensoren - kontaktlosen Sensoren - Ohrthermometer - Glatteiswarnsysteme
Pyrometer
Temperaturen messen mit Genauigkeiten von +/- 0,1%
https://www.elektronikpraxis.vogel.de/temperaturen-messen-mit-genauigkeiten-von-01-c-a-1105348/
http://www.suessbrich.info/elek/Bauanleitung_Thermo.pdf
300_b_fritz-x_Messen von Temperaturen mit Halbleitern LM35 LM135 LM235 LM335 oder npn-Transistor_1a.pdf
http://www.suessbrich.info/elek/elektherm1.html Messen und Regeln von Temperaturen mit Halbleitern Welchen Sensor nimmt man wann? Ein kurzer Ratgeber 300_b_fritz-x_Auswahl Temperatursensoren - Welche Temperatursensoren nimmt man wann!_1a.pdf
https://de.wikipedia.org/wiki/Thermoelement
https://de.wikipedia.org/wiki/Halbleiter-Temperatursensor http://www.ti.com/lit/ds/symlink/lm335.pdf
********************************************************I*
1) Beachte die unterschiedliche Schreibweise von Zahlen ! . , ^ E+03 E-03
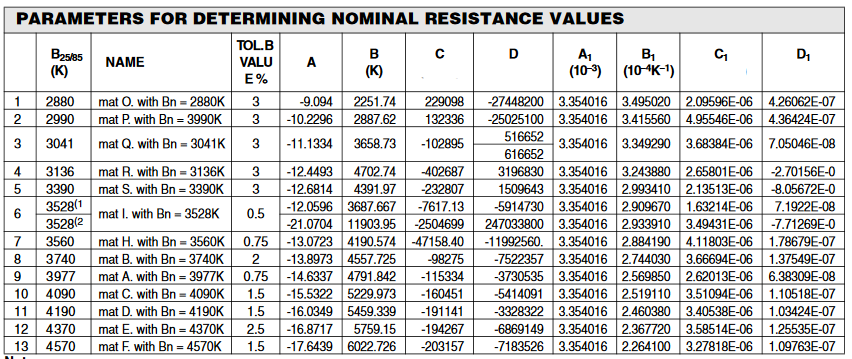
For the 10k-2 Thermistor the "B" constants over the 0°C to 70°C temperature range are;
Europa USA
B0 = -5,380125E+00 -5,380125 ( -5.380125 )
B1 = 4,777517E+03 4777,517 (4,777.517) B2 = -1,2001468E+05 -120014,68 (-120,014.68) B3 = -2,168775E+06 -2168775 (-2,168,775) B1= 0,000256985 2.56985E-04 C1 = 0,000002620131 2.620131E-06 D1= 0,00000006383091 6.383091E-08 und allgemein in englischsprachigen Ländern "log" zur Basis e ist, also dem deutschen "ln" entspricht. Vielleicht ist "ln" sogar nur in deutschsprachigen Ländern gebräuchlich ! ! !
ln = Natural Log (Log to the Napierian base 2.718281828...)
=1/( A1 + (B1*ln(F1/E1)) + (C1*(ln(F1/E1)^2)) + (D1*(ln(F1/E1)^3)) ) ln = RICHTIG
=1/( A1 + (B1*log(F1/E1)) + (C1*(log(F1/E1)^2)) + (D1*(log(F1/E1)^3)) ) log = in Europa FALSCH
T=1/( A1 + (B1*LOG(F1/E1)) + (C1*(LOG(F1/E1)^2)) + (D1*(LOG(F1/E1)^3)) )
T=1/( A1 + (B1*LN(F1)) + (C1*(LN(F1)^2)) + (D1*(LN(F1)^3)) )
e = 2,718281828459 Eulersche-Zahl
wobei exp EXP die Umkehrung von ln im natürlichen Logarithmus ist.
EXP ODER e ^
Rt = R25 * exp ( B * (1/T1 - 1/T2 )
Rt = R25 * e ^ ( B * (1/T1 - 1/T2 )
Rt =10000*EXP(4000*(1/(273,15+0) - 1/(273,15+25))) = 34140,6 Ohm bei 0 °C
Rt =10000*2,718281828459^(4000*(1/273,15 - 1/298,15)) = 34140,6 Ohm bei 0 °C
Rt = R25 * exp ( B * (T2-T1) / (T2*T1) )
Rt = R25 * e ^ ( B * (T2-T1) / (T2*T1) )
Rt =10000*EXP(4000*((273,15+25) - (273,15+0)) / ((273,15+25) * (273,15+0))) = 34140,6 Ohm bei 0 °C
Rt =10000*2,718281828459^(4000*((273,15+25) - (273,15+0)) / ((273,15+25) * (273,15+0))) = 34140,6 Ohm bei 0 °C
R25 = 10k
T1= 0 °C = 273,15K ist die aktuelle zu messende Temperatur in Kelvin Grad.
T2 = 25 °C = 298,15K ist die NTC Referenztemperatur bei 25 °C aber in Kelvin
Es kommen die unterschiedlichsten Schreibweisen von Formeln und Bezeichnungen vor T2 = R0 = Rt = Rref = R25 = 10000 Ohm bei NTC 10k bei Normtemperatur von 25°C R25 = 10k TC R0 Nennwiderstand in Ohm bei 25 °C B25/75 = 4000K Exponentensteigung in Ohm
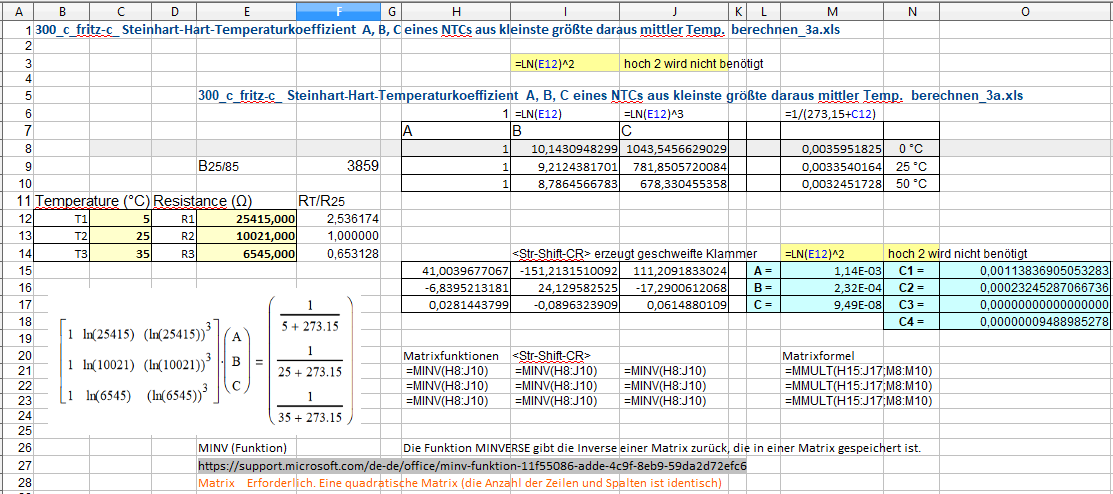
Das Polynom (1) von Extended Steinhart
(1) Wir betrachten Nominalwerte und ignorieren Minimal- und Maximalwerte.
Da es vier Koeffizienten gibt, müssen wir ein System von vier Gleichungen wie folgt erstellen:
wo wir eine Tabelle mit Widerstandsmessungen findenbei bekannten Temperaturen (1).
(1) Wir betrachten Nominalwerte und ignorieren Minimal- und Maximalwerte.
Aus dieser Tabelle entnehmen wir vier Werte, die möglichst weit auseinander liegen sollten.
T1 = 0 °C R1 = 35563
T2 = 25°C R2 = 10000
T3 = 50 °C R3 = 3336,3
T4 = 100°C R4= 549,4
300_c_fritz-x_NTC Widerstand B57164 K164 10k B25=4300K - Normierte R-T-Kennlinien_1a.xls
Jetzt kennen wir die Werte für Widerstand und Temperatur und können die Koeffizienten A, B, C und D berechnen.
300_fritz-x_Steinhart–Hart Coefficients Calculator - North Star Sensors_4a.xls
calculation-003_1.pdf
T =1 / ( A1 + (B1*LN(F1)) + (C1*(LN(F1)^2)) + (D1*(LN(F1)^3)) )
vereinfacht
T1 = 0 °C R1 = 35563
T2 = 25°C R2 = 10000
T3 = 50 °C R3 = 3336,3
300_c_fritz-x_NTC Widerstand B57164 K164 10k B25=4300K - Normierte R-T-Kennlinien_1a.xls Jetzt kennen wir die Werte für Widerstand und Temperatur und können die Koeffizienten A, B, C und D berechnen.
T =1 / ( A1 + (B1*LN(E1)) + (C1*(LN(E1)^3)) )
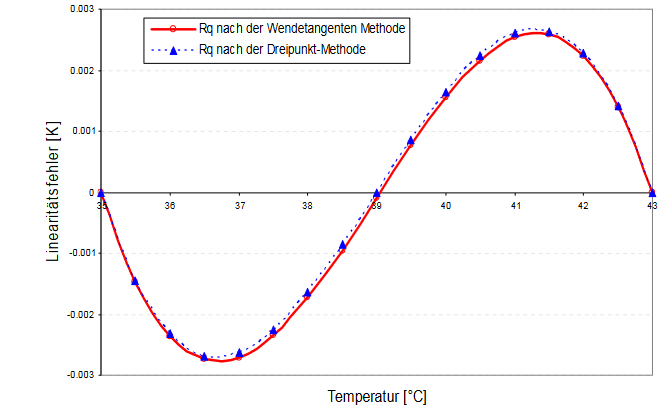
2k2 Ohm bei 25 °C,
10k Ohm bei 25 °C
47k Ohm bei 25 °C
NTC & PTC
INHALTSVERZEICHNIS
0) Temperaturmessung mit Temperatursensoren / Temperaturfühler
Analog Digital Sensoren
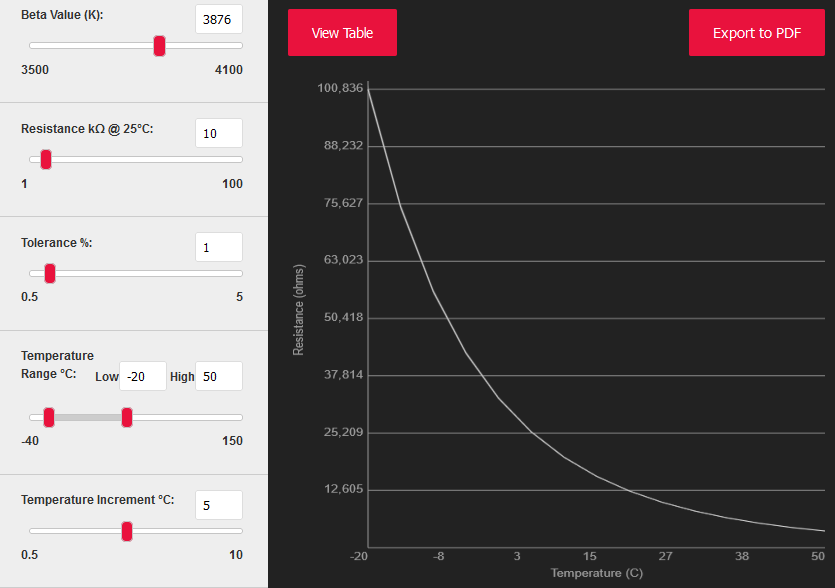
1.0) Unbekannten NTC Widerstand berechnen und messen! (1A)
B-Wert = NTC Thermistorkonstante berechnen z.B. B25/50= 3976K 1.1) NTC (Temperatursensoren) B-Wert berechnen 1.2) NTC-Spannungsteiler Lookuptable Koeffizienten-Version A, B, C, D - A1, B1, C1, D1 1.3) Calculate the Resistance of an NTC at different Temperatures Widerstand - Spannung Untc - Strom ntc - Leistung ntc - Erwärmung ntc
2) Steinhart and Hart Calculator
a, b, c Coeffizient - DR/DT - alpha - beta eines NTC Thermistor berechnen. 3) Steinhart-Hart Thermistor Calculator (Rechner)
4.0) Unbekannten NTC Widerstand berechnen und messen!
4.1) Steinhart-Hart-Thermistor Calculator Konstanten A, B, C, D 4.2) Temperaturmessung mit NTC Thermistoren B-Konstanten B0, B1, B2, B3, B4 Koeffizienten A, B, C 5) Thermistor Calculator LabJack Corporation (1A) A, B, C, D aus der Tabelle 6) Steinhart-Hart Temperature Calculator Coeffizient A, B, C 7) Diverse Calculators NE555 - Impedanz - LM317 - Ohm - LED - LM3914 - LM3915 - Thermistor 8) Si7013 Thermistor Correction CalculatorBerechnung des Thermistorfehlers 9) Steinhart and Hart Calculator Koeffizient A, B, C
10) NTC R/T Calculation 5.0 - Web-basierte Anwendung (1A)
TDK Electronics NTC R/T Tabellen-Ersteller z.B. B57332V5103F360 10k 1%
11.0) NTC Thermistor Resistance Calculator V2.0
Ohm und Vout 11.1) NTC Thermistor Resistance Calculator V2.0 Ohm und Vout mit Diagramm 12) Voltage Divider Circuit Calculator - For NTC Thermistor Ohm und Vout 13.0) Potenzialteiler mit NTC-Thermistor Ohm und Vout mit B25/75
13.1) Qti Thermistor R/T Calculators (1A) Online Rechner
A, B, C Coeffizients Rechner
13.2) LaserCalculator - NTC thermistor calculator
14) VISHAY NTC RT Calculation ToolTabellen erstellen mit A, B, C Coeffizienten
15) Thermistors and Sensor CalibrationTabelle a, b, c 16) Thermistor with Series and Parallel Resistor (1A) Excel-Rechenformular Tabellenwerte zu Rechenwerte 17) Thermistor Coefficient Calculator for TI Advanced Fuel Gauges Texas Instruments Berechnung der A0, A1, A2, A3 Coeffizienten 18) Leitfaden zur Auswahl der NTC WiderstandswerteFormeln 19) NTC Thermistor Tools - Table Generator NTC Thermistor Tabellen Erzeuger
20) SELF-CALIBRATE YOUR THERMISTORS
Formeln
21.0) Calculating Temperature from Resistance (A B C D Koeffizienten)
North Star Sensors Steinhart-Hart A, B, C,D Coeffizienten Rechner
21.1) Berechnen der Temperatur aus dem Widerstand
North Star Sensors Steinhart-Hart Formeln und Tabellen 22) Thermistor Calculator Adrien RICCIARDI ADC value 23) ARDUINO Temperaturmessung mit NTC-the Steinhart-Hart Formula Formeln B- oder β- Parametergleichung Sketch 24) Präzise Temperaturmessung mit 12bit-ADC und NTC
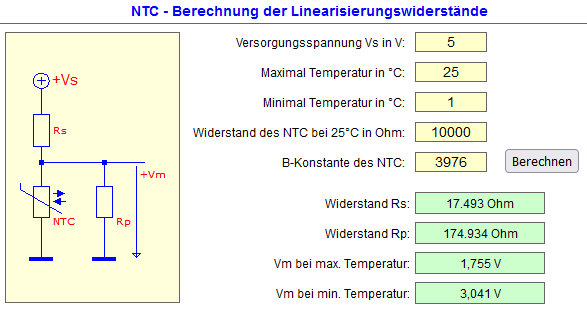
25) NTC als Spannungsteiler linearisieren?
Reihen- und Parallel-Schaltung 26) NTC-Thermistor Parameter - B Wert Beschreibung & Berechnungsmethode Der B-Wert ist der Wärmekoeffizient des Thermistors mit negativem Temperaturkoeffizienten. 27) Steinhart-Hart-Thermistorkalibrierung in Excel mit Matrixformel 28) NTC-Berechnung (1A) Excel-Formeln Diagramm Linearisierung 29) Linearisierung von resistiven Sensoren Spannungsquelle oder Stromquelle
30) Sensordateien für einfache Sensoren
NTC und LDR 31) 10k NTC - Mikrocontroller.net NTC-Tabelle_1a.xls (1A) Excel-Formeln Diagramm Linearisierung Mikrocontroller 32) Steinhart-Hart-Gleichung Formeln 33) Steinhart-Hart NTC - Links
https://www.mathscinotes.com
https://www.newport.com https://www.cypress.com https://qastack.com.de https://www.computerwissen.de 34) ARDUINO NTC lesen - Gunther Breu Arduino Sketch 35) NTC-Widerstände - Grundlagen (1A)Reihen- und Parallel-Schaltung - Tabellen-Generator 36) Linearisierung eines NTC mit 2 Widerständen Linearisierung mit Reihen- und Parallel-Schaltung 37) WeTec's Technikseite NTC & PTC Online-Rechner 38) NTC - Berechnung der LinearisierungswiderständeElectronic Developer Online calculator 39) SEBULLI Code Generator für eine NTC-Tabelle NTC-Tabellen Code Generator für eine
40) Potentiometer mit Parallelwiderstand - WeTec's Technikseite
Zwei Widerstände parallel zu einem linearem Potentiometer geschaltet ergibt logarithmische Kennlinie 41) NTC Thermistor Heißleiter Linearisierung mit sogar 3 Widerständen
42) Bauen und Programmieren von AVR-Mikrocontrollern ATMega8Diagramm
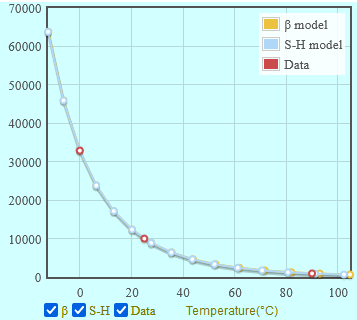
43) NTC Heißleiter Berechnung nach Formel Online-Berechnung 44.0) SRS Thermistor Calculator 1.10 mit Diagramm R-T - A, B, C - S-H model B25/75 = beta modell
44.1) NTC Thermistors Steinhart and Hart Equation
Thermistorcalc Berechnung mit A, B, C coeffizient 44.2) NTC Thermistors Berechnung von b-Wert Beta Wert B25/50 44.3) NTC Thermistor Beta Value Calculator b-Wert Beta-Wert B25/50 45) Steinhart-Hart Thermistor Calibration in Excel 46) NTC thermistor calculator
47) BUCH: Sensorschaltung -Simulation mit PSPICE
48.0) Steinhart-Hart Calculation Example
48.1) Arduino Tutorial: Der Temperatursensor mit NTC
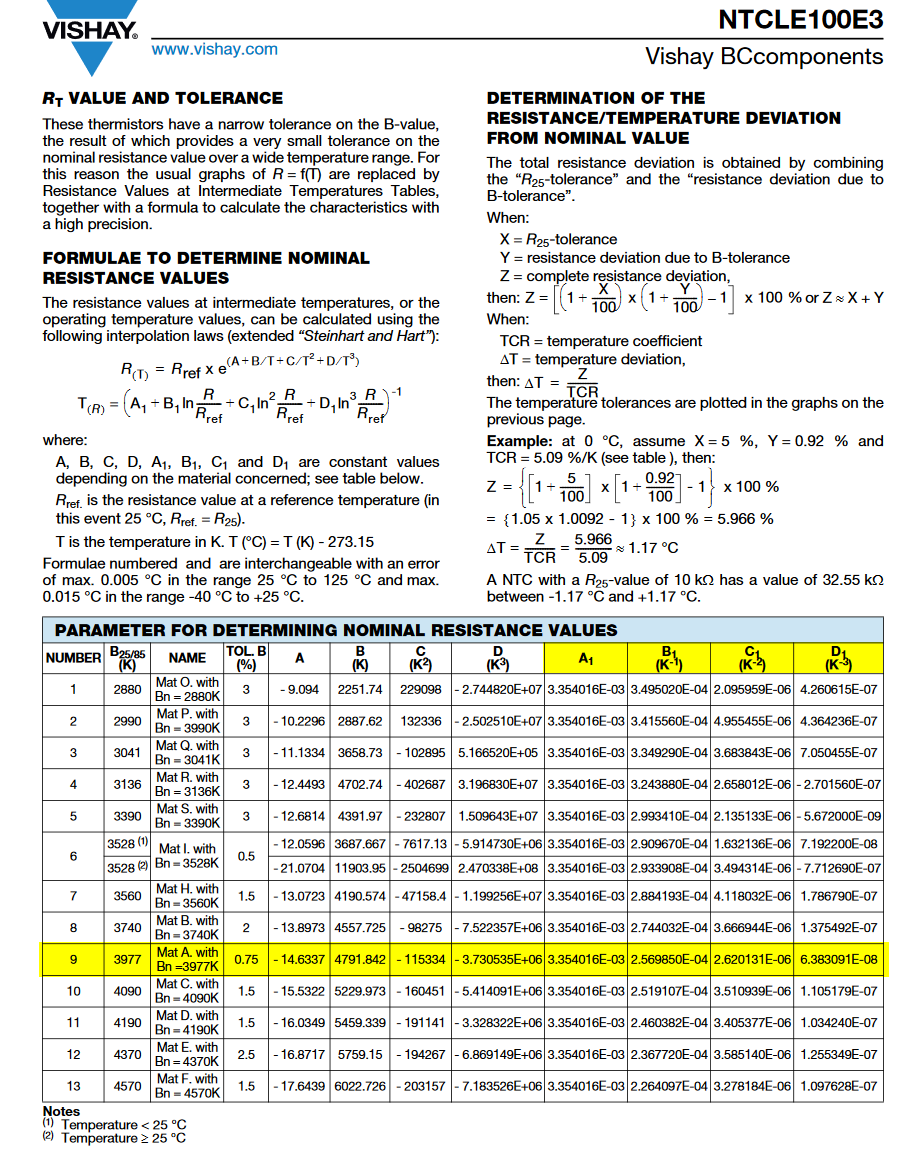
Sketch 48.2) VISHAY Konstanten A1, B1, C1, D1 Constante A, B, C, D - A1, B1 C1, D1 49) BUCH: Ausgewählte Sensorschaltungen - Vom Datenblatt zur Simulation
50) Linearisierung von resistiven Sensoren/ Heissleiter
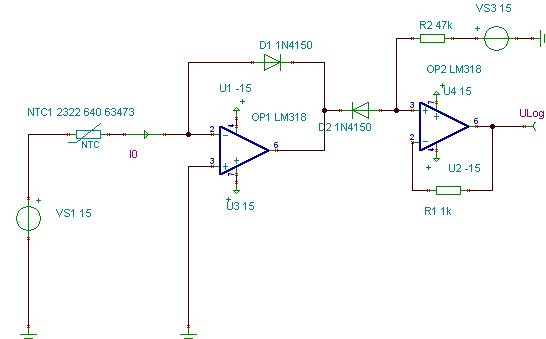
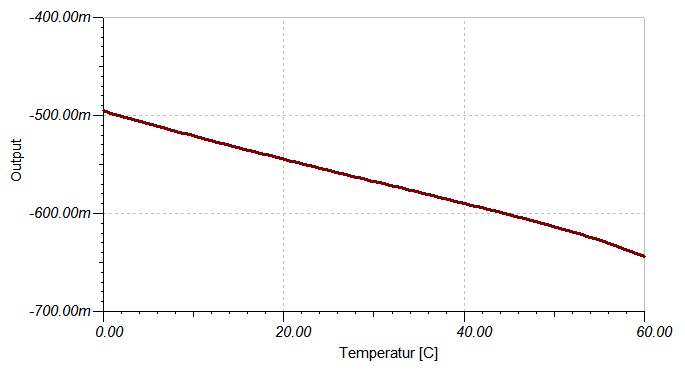
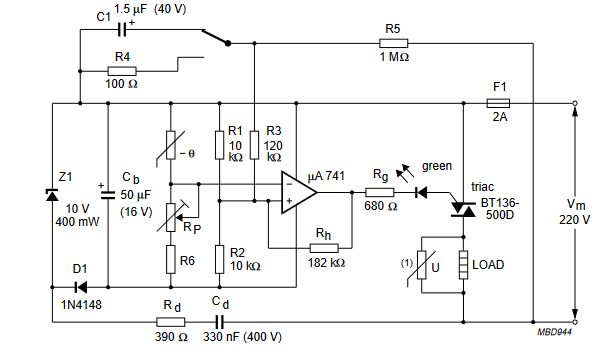
Linearisierung mit Op-Amp und Dioden 1N5150 51) 230Vac Kühlschrankthermostat mit NTC-Temperatursensor NTC47k Op-Amp uA741 BT136-500D 52) NTC Wert unruhig (solved)
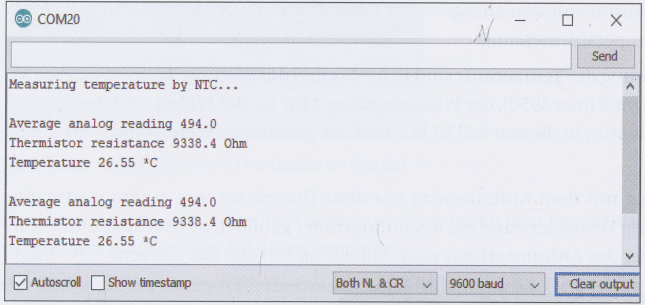
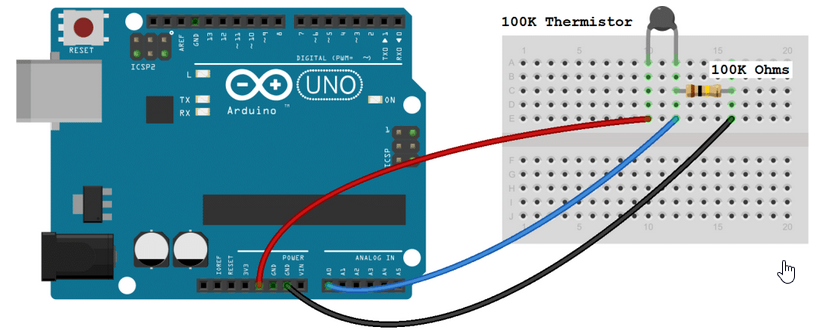
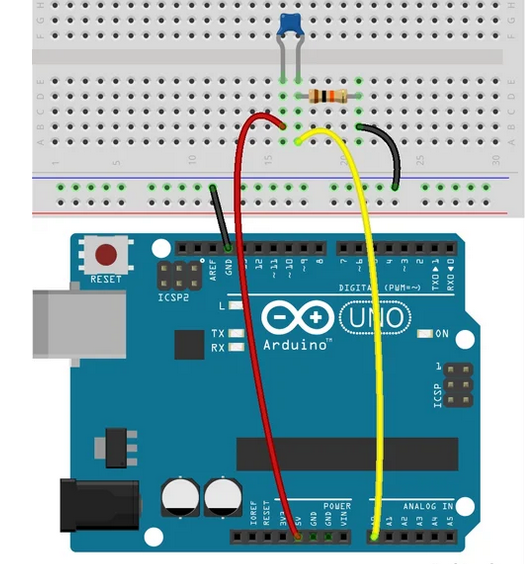
53) ARDUINO Temperaturmessung mit NTC 10k
54) Arduino Temperatur analog messen mit einem NTC
Sketch 55) ARDUINO Temperaturmessung mit einem 10k NTC Sketch 56) Arduino Tutorial: Der NTC Temperatursensor Sketch 57) BUCH: ARDUINO - Das umfassende Handbuch
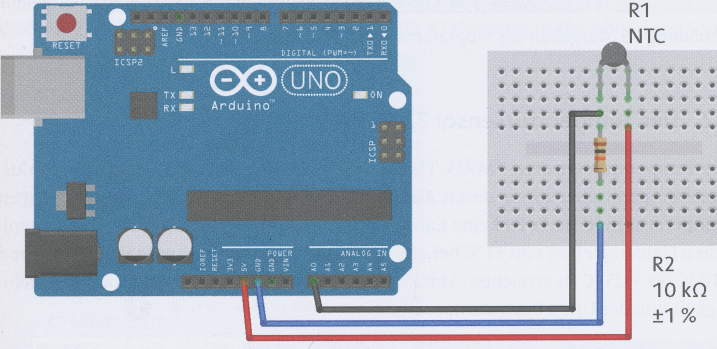
58) NTC-Thermistor am ARDUINO UNO R3
Sketch
59.0) Arduino Lektion 84: NTC-Widerstand (Heißleiter)
59.1) Thermistor adafruit learning system ARDUINO UNO
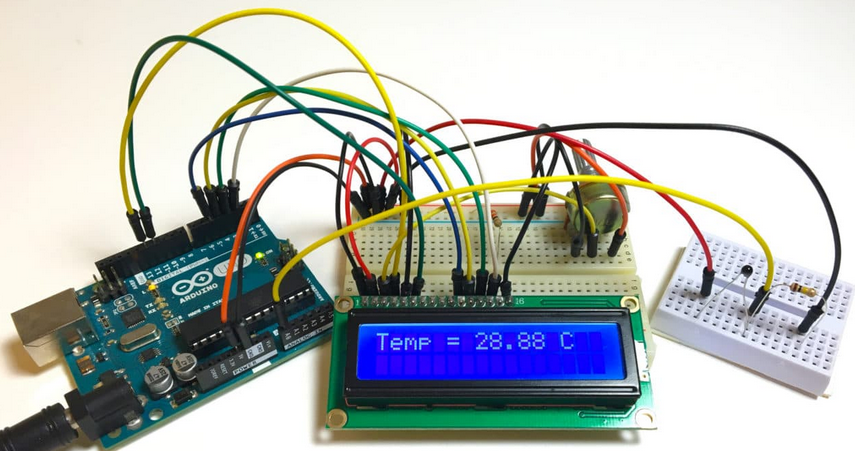
Tabelle - Sketch 60) Make an Arduino Temperature Sensor (Thermistor Tutorial) Sketch 61) 10k THERMISTOR WITH ARDUINO UNO R3 Thermistor.ino Sketch 62) Make an Arduino Temperature Sensor (Thermistor Tutorial) Thermistor Sketch mit LCD Anzeige
63) Arduino Temperatur analog messen mit einem NTC
YouTube 64) Wie berechne ich die Temperatur eines NTC Sensors Excel Formeln mit Linearitäts-Diagramm 65) Arduino Tutorial: Der Temperatursensor Formeln - Sketch 66) Nr.10 Temperatur messen Formeln - Sketch 67) Wie messe ich die Temperatur mit einem Arduino Uno? 68) Arduino Lektion 84: NTC-Widerstand (Heißleiter) 69) Arduino Lektion 48: Temperatursensor DS18B2070)
5.1 - Temperaturmessung mit einem 10kΩ NTC Wiederstand
70)
71) NTC-Thermistor-Testverfahren für Fahrzeug-Klimaanlage 72) NTC-Thermistor Parameter - B Wert Beschreibung & Berechnungsmethode
73) XVI Temperaturanzeige und Simulation
Sketch 74) Bestimmung der Messunsicherheiten bei der Temperaturmessung 75) Bestimmung von Thermometerkennlinien 76) Physikalische Trainingsaufgaben
77) Regression des Widerstands eines Thermistors
Formeln - Regressionswerte: A, B, C, D 78) Calibrate Steinhart-Hart Coefficients for Thermistors
79) NTC Temperatursensor am wired 12/14 IO-Modul
Excel-Tabelle VISHAY NTCLE100E3103JB0
80) NTC Thermistor Widerstandsrechner
81)Thermistor Rechner Datenblatt PDF
Sketch
82) SOURCEFORGE
83) EFI Testen eines unbekanten NTC Thermistors
Online Rechner A, B, C 84) Temperaturen mit dem TMP36 und ARDUINO messen Sketch 85) Temperaturen mittels Thermistor und seriellen Plotter der Arduino IDE als Graph darstellen 86) Hohe Temperaturen bis 1000°C mit dem MAX6675 und einem Thermoelement vom Typ-K mit dem Arduino messen 87) DHT11 & DHT22 Sensoren zur Messung von Temperatur und Feuchte mit dem Arduino im Vergleich 88) Präzise analoge Spannungsmessungen mit dem Arduino anhand einer Referenzspannung messen 89) Drei Methoden zur Filterung von verrauschten ADC-Messungen mit dem Arduino
90) Arduino Lektion 44: BME280 Temperatur, Luftfeuchtigkeit und Luftdruck Sensor
91) Digital thermometer with Arduino and LM335 temperature sensor 92) Ein Sieben-Segment Display direkt mit dem Arduino ansteuern 93) Aufzeichnen serieller Daten vom Arduino in eine Log-Datei auf dem PC 94) Die Feuchtigkeit in der Erde / Boden mit dem Arduino UNO messen. 95) Mit dem Arduino alle angeschlossenen I2C / TWI Adressen scannen 96) Das Schema und Funktionsprinzip des Thermistors 97) Wie man mit Thermistoren die Temperatur genau messen kann
98) How to Measure Temperature with an NTC Thermistor
Sketch 99) ARDUINO - Messen der Temperatur mit einem NTC-Thermistor
100) Wie erhalte ich A-, B-, und C-Werte für diesen Thermistor? 101) NTC-TemperatursensorenSketch 102) Technische Temperaturmessung (1A)
103) NTC-Tabelle - Werte aus Datenblätter
104) Widerstands- und Temperaturwerte B25/85 beta-Berechnung 105) Thermistors and NTC Thermistors
106) Handy-App Thermometer Calculator Matthew Vernon Was ist ein NTC-Thermistor?107) Completely Integrated, 0.1°C Thermistor Measurement System 108) Arduino Measuring temperature with NTC – Steinhart-Hart Formula 109) Measuring temperature with NTC-The Steinhart-Hart Formula 110) elektor Differenz-Temperaturindikator
********************************************************I*
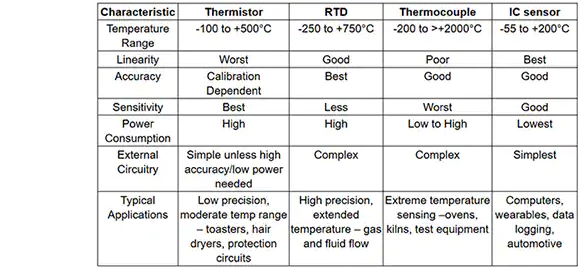
Ein NTC-Widerstand, auch NTC-Thermistor genannt, ist ein Widerstand mit einem negativen Temperaturkoeffizienten, was bedeutet, dass der Widerstand mit steigender Temperatur abnimmt.
NTC steht für „Negativer Temperaturkoeffizient“ (eng.: „Resistance Temperature Detectors“).
Abbildung 1: NTC-Widerstand Schalt-Symbol
Sie werden in erster Linie als resistive Temperatursensoren und Strombegrenzungsvorrichtungen verwendet.
Der Temperaturempfindlichkeitskoeffizient ist etwa 5x größer als der von Silizium-Temperatursensoren (Silistoren) und etwa 10x größer als der von Widerstandstemperaturfühlern (RTDs).
NTC-Sensoren werden typischerweise in einem Bereich von -55°C bis 200°C eingesetzt.
Die Nichtlinearität des Verhältnisses zwischen Widerstand und Temperatur bei NTC-Widerständen stellte bei der Verwendung von Analogschaltungen zur genauen Temperaturmessung eine große Herausforderung dar, aber die rasche Entwicklung digitaler Schaltungen löste dieses Problem und ermöglichte die Berechnung präziser Werte durch Interpolation von Nachschlagetabellen oder durch Lösung von Gleichungen, die eine typische NTC-Kurve approximieren. Eigenschaften des NTC-Widerstand Im Gegensatz zu RTDs (Resistance Temperature Detectors), die aus Metallen bestehen, werden NTC-Thermistoren im Allgemeinen aus Keramik oder Polymeren hergestellt. Unterschiedliche verwendete Materialien führen zu unterschiedlichen Temperaturreaktionen sowie zu anderen Eigenschaften.
Temperatur-Ansprechverhalten
Während die meisten NTC-Thermistoren typischerweise für den Einsatz in einem Temperaturbereich zwischen -55 °C und 125 °C geeignet sind, wo sie ihre präzisesten Messwerte liefern, gibt es spezielle Familien von NTC-Thermistoren, die bei Temperaturen nahe dem absoluten Nullpunkt (-273,15 °C) eingesetzt werden können, sowie solche, die speziell für den Einsatz über 150 °C ausgelegt sind. Die Temperaturempfindlichkeit eines NTC-Sensors wird als „prozentuale Änderung pro Grad C“ ausgedrückt.
Abhängig von den verwendeten Materialien und den Besonderheiten des Produktionsprozesses reichen die typischen Werte der Temperaturempfindlichkeiten von -3% bis -6% pro °C.
Abbildung 2: Widerstands-Temperatur-Charakteristik eines NTC-Widerstand
Wie aus der Abbildung 2 ersichtlich ist, haben die NTC-Thermistoren im Vergleich zu den RTDs aus Platinlegierung einen viel steileren Widerstands-Temperaturverlauf, was zu einer besseren Temperaturempfindlichkeit führt.
Trotzdem sind RTDs mit einer Genauigkeit von ±0,5% der gemessenen Temperatur nach wie vor die genauesten Sensoren, und sie eignen sich für den Temperaturbereich zwischen -200 °C und 800 °C, ein viel größerer Bereich als der der NTC-Temperatursensoren.
Vergleich mit anderen Temperatursensoren Im Vergleich zu FTE haben die NTCs eine kleinere Größe, schnelleres Ansprechverhalten, größere Schock- und Vibrationsfestigkeit bei geringeren Kosten.
Dafür sind sie etwas weniger präzise als RTDs.
Im Vergleich zu Thermoelementen ist die von beiden erzielte Präzision ähnlich;
jedoch können Thermoelemente sehr hohen Temperaturen (in der Größenordnung von 600°C) standhalten und werden in solchen Anwendungen anstelle von NTC-Thermistoren verwendet, wo sie manchmal als Pyrometer bezeichnet werden.
Dennoch bieten NTC-Thermistoren bei niedrigeren Temperaturen eine höhere Empfindlichkeit, Stabilität und Genauigkeit als Thermoelemente und werden mit weniger zusätzlichen Schaltungen und daher zu geringeren Gesamtkosten eingesetzt.
Die Kosten werden zusätzlich durch den Wegfall von Signalkonditionierungsschaltungen (Verstärker, Pegelumsetzer usw.) gesenkt, die bei RTDs oft benötigt werden und bei Thermoelementen immer erforderlich sind.
Selbsterwärmungseffekt Der Selbsterwärmungseffekt ist ein Phänomen, das immer dann auftritt, wenn ein Strom durch den NTC-Widerstand fließt.
Da der Thermistor im Grunde ein Widerstand ist, gibt er Leistung als Wärme ab, wenn ein Strom durch ihn fließt.
Diese Wärme wird im Thermistorkern erzeugt und beeinträchtigt die Genauigkeit der Messungen.
Das Ausmaß, in dem dies geschieht, hängt von der Menge des fließenden Stroms, der Umgebung (ob es sich um eine Flüssigkeit oder ein Gas handelt, ob es einen Fluss über den NTC-Sensor gibt usw.), dem Temperaturkoeffizienten des Thermistors, der Gesamtfläche des Thermistors usw. ab.
Die Tatsache, dass der Widerstand des NTC-Sensors und damit der Strom durch ihn von der Umgebung abhängt, wird häufig bei Flüssigkeitsanwesenheitsmeldern, wie sie
z.B. in Lagertanks zu finden sind, genutzt.
NTC-Widerstand Wärmekapazität
Die Wärmekapazität stellt die Wärmemenge dar, die erforderlich ist, um die Temperatur des Thermistors um 1°C zu erhöhen, und wird normalerweise in mJ/°C ausgedrückt.
Die Kenntnis der genauen Wärmekapazität ist bei der Verwendung eines NTC-Thermistorfühlers als Einschaltstrombegrenzer von großer Bedeutung, da sie die Ansprechgeschwindigkeit des NTC-Temperaturfühlers definiert.
Auswahl und Berechnung Thermistoren Bei der sorgfältigen Auswahl müssen Dissipationskonstante, thermische Zeitkonstante, Widerstandswert, Widerstands-Temperatur-Kurve und Toleranzen des NTC-Widerstand berücksichtigt werden, um die wichtigsten Faktoren zu nennen. Da die Beziehung zwischen Widerstand und Temperatur (die R-T-Kurve) hochgradig nichtlinear ist, müssen beim praktischen Systemdesign bestimmte Näherungen verwendet werden.
1) Approximation erster Ordnung
Eine Annäherung, die am einfachsten zu verwenden ist, ist die Annäherung erster Ordnung, die besagt, dass:
Dabei ist k der negative Temperaturkoeffizient, ΔT die Temperaturdifferenz und ΔR die aus der Temperaturänderung resultierende Widerstandsänderung.
Diese Näherung erster Ordnung ist nur für einen sehr engen Temperaturbereich gültig und kann nur für solche Temperaturen verwendet werden, bei denen k über den gesamten Temperaturbereich nahezu konstant ist.
2) Beta-Formel Eine weitere Gleichung liefert zufriedenstellende Ergebnisse, die auf ±1°C über den Bereich von 0 °C bis +75 °C genau sind.
Sie ist abhängig von einer einzigen Materialkonstante β, die durch Messungen erhalten werden kann.
Die Gleichung kann wie folgt geschrieben werden:
Dabei ist R(T) der Widerstand des Thermistor bei der Temperatur T in Kelvin, R(T0) ist ein Referenzpunkt bei der Temperatur T0.
Die Beta-Formel (B25/75) erfordert eine Zweipunktkalibrierung, und sie ist typischerweise nicht genauer als ±5°C über den gesamten Nutzbereich des NTC-Thermistors.
3)Steinhart-Hart-Gleichung
Die beste bisher bekannte Annäherung ist die 1968 veröffentlichte Steinhart-Hart-Formel: Dabei ist ln R der natürliche Logarithmus des NTC-Widerstand bei der Temperatur T in Kelvin, und A, B und C sind aus experimentellen Messungen abgeleitete Koeffizienten.
Diese Koeffizienten werden normalerweise von Thermistorherstellern als Teil des Datenblatts veröffentlicht.
Die Steinhart-Hart-Formel ist typischerweise auf etwa ±0,15°C über den Bereich von -50°C bis +150°C genau, was für die meisten Anwendungen ausreichend ist.
Wenn eine höhere Genauigkeit erforderlich ist, muss der Temperaturbereich reduziert werden, und eine Genauigkeit von besser als ±0,01°C über den Bereich von 0°C bis +100°C ist erreichbar ?
Auswahl der richtigen Annäherung Die Wahl der Formel, die zur Ableitung der Temperatur eines NTC-Widerstand aus der Widerstandsmessung verwendet wird, muss sich nach der verfügbaren Rechenleistung sowie den tatsächlichen Toleranzanforderungen richten.
In einigen Anwendungen ist eine Näherung erster Ordnung mehr als ausreichend, während in anderen Anwendungen nicht einmal die Steinhart-Hart-Gleichung die Anforderungen erfüllt, und der NTC-Widerstand muss Punkt für Punkt kalibriert werden, wobei eine große Anzahl von Messungen durchgeführt und eine Nachschlagetabelle erstellt werden muss.
Aufbau und Eigenschaften von NTC-Thermistoren
Materialien, die typischerweise an der Herstellung von NTC-Widerständen beteiligt sind, sind Platin, Nickel, Kobalt, Eisen und Siliciumoxide, die als reine Elemente oder als Keramiken und Polymere verwendet werden.
NTC-Thermistoren können je nach dem verwendeten Herstellungsverfahren in 3 Gruppen eingeteilt werden.
NTC-Widerstand in Perlen-Bauweise.
1) Perlen-Thermistoren
Diese NTC-Thermistoren werden aus direkt in den Keramikkörper eingesinterten Bleidrähten aus Platinlegierung hergestellt.
Sie bieten im Allgemeinen schnelle Ansprechzeiten, bessere Stabilität und ermöglichen den Betrieb bei höheren Temperaturen als Scheiben- und Chip-NTC-Sensoren, sind jedoch zerbrechlicher.
Es ist üblich, sie in Glas zu versiegeln, um sie vor mechanischer Beschädigung während der Montage zu schützen und ihre Messstabilität zu verbessern.
Die typischen Größen reichen von 0,075 – 5 mm Durchmesser.
NTC-Widerstand in Scheiben-Bauform
2) Scheiben- und Chip-Thermistoren Diese NTC-Thermistoren haben metallisierte Oberflächenkontakte.
Sie sind größer und haben daher eine langsamere Reaktionszeit als NTC-Widerstände vom Perlentyp.
Aufgrund ihrer Größe haben sie jedoch eine höhere Verlustleistungskonstante (Leistung, die erforderlich ist, um ihre Temperatur um 1°C zu erhöhen), und da die Verlustleistung des Thermistors proportional zum Quadrat des Stroms ist, können sie höhere Ströme viel besser bewältigen als Perlthermistoren.
Scheibenthermistoren werden hergestellt, indem eine Mischung von Oxidpulvern in eine runde Form gepresst wird, die dann bei hohen Temperaturen gesintert wird.
Chips werden normalerweise durch ein Bandgussverfahren hergestellt, bei dem eine Aufschlämmung des Materials als dicker Film ausgebreitet, getrocknet und in Form geschnitten wird.
Die typischen Größen reichen von 0,25-25 mm im Durchmesser.
Ein glasgekapselter NTC-Widerstand
Glasgekapselte NTC-Thermistoren Dabei handelt es sich um NTC-Temperatursensoren, die in einer luftdichten Glasblase eingeschlossen sind.
Sie sind für den Einsatz bei Temperaturen über 150°C oder für die Leiterplattenmontage vorgesehen, wo Robustheit ein Muss ist.
Die Einkapselung eines Thermistors in Glas verbessert die Stabilität des Sensors und schützt ihn gleichzeitig vor der Umgebung.
Sie werden durch hermetisch versiegelte NTC-Widerstände vom Wulsttyp in einem Glasbehälter hergestellt.
Die typischen Größen reichen von 0,4-10 mm im Durchmesser.
Typische Anwendungen für NTC-Widerstände NTC-Thermistoren werden in einem breiten Spektrum von Anwendungen eingesetzt.
Sie werden zur Temperaturmessung, Temperaturregelung und zur Temperaturkompensation eingesetzt.
Sie können auch zur Erkennung des Fehlens oder Vorhandenseins einer Flüssigkeit, als Strombegrenzungsvorrichtungen in Stromversorgungskreisen, zur Temperaturüberwachung in Automobilanwendungen und vieles mehr eingesetzt werden.
NTC-Sensoren können in 3 Gruppen unterteilt werden, je nach der in einer Anwendung ausgenutzten elektrischen Eigenschaft.
1. Widerstands-Temperatur-Charakteristik
Zu den Anwendungen, die auf der Widerstands-Zeit-Kennlinie basieren, gehören Temperaturmessung, -regelung und -kompensation.
Dazu gehören auch Situationen, in denen ein NTC-Widerstand verwendet wird, so dass die Temperatur des NTC-Temperaturfühlers mit einigen anderen physikalischen Phänomenen zusammenhängt.
Diese Gruppe von Anwendungen erfordert, dass der Thermistor im leistungslosen Zustand arbeitet,
d.h. dass der Strom durch den Thermistor so gering wie möglich gehalten wird, um eine Erwärmung des Fühlers zu vermeiden.
2. Strom-Zeit-Kennlinie Anwendungen, die auf der Strom-Zeit-Kennlinie basieren, sind:
Zeitverzögerung, Einschaltstrombegrenzung, Überspannungsunterdrückung und viele andere.
Diese Eigenschaften hängen mit der Wärmekapazität und der Verlustleistungskonstante des verwendeten NTC-Thermistors zusammen.
Die Schaltung ist normalerweise darauf angewiesen, dass sich der NTC-Thermistor aufgrund des durch ihn fließenden Stroms erwärmt.
Irgendwann löst er je nach der Anwendung, in der er eingesetzt wird, eine Art Änderung in der Schaltung aus.
3. Spannungs-Strom-Kennlinie
Anwendungen, die auf der Spannungs-Strom-Kennlinie eines Thermistors basieren, beinhalten im Allgemeinen Änderungen der Umgebungsbedingungen oder Schaltungsvariationen, die zu Änderungen des Arbeitspunktes auf einer gegebenen Kurve in der Schaltung führen.
Je nach Anwendung kann dies für Strombegrenzung, Temperaturkompensation oder Temperaturmessungen genutzt werden.
Quelle: Carsten Hack ist begeisterter Hobby-Bastler
https://www.e-hack.de/was-ist-ein-ntc-widerstand-eine-definition/
Steinhart-Hart-Gleichung
Die Koeffizienten A0 A1 A2 A3 und werden als Steinhart-Hart-Koeffizienten bezeichnet.
Die Bezeichnung A B C D wird auch verwendet.
Findet man in Tabellen nur 3 Koeffizienten dann bei C 0 eingeben
Für praktische Anwendungen haben nur 3 Terme mit den Koeffizienten A0 A1 A2 A3 A4 A5 A6 .... eine Bedeutung, die restlichen Koeffizienten sind in Relation so klein, dass sie für praktische Anwendungen im Bereich der Messtechnik im Messbereich um 0 °C bis +70 °C vernachlässigt werden können.
Der Steinhart-Hart-Temperaturkoeffizient des Thermistors kann den Wert von A, B, C über die obigen 3 Temperaturpunkte berechnen.
1. Temperatur-Widerstandskurve
Geben Sie drei Datensätze gemäß den tatsächlichen Daten (R1, T1), (R2, T2) und (R3, T3) ein, die unter verschiedenen Temperatur bedingungen gemessen werden müssen.
Das beste Ergebnis von Datenauswahl punkten ist die Auswahl der beiden Endpunkte und des Mittelpunkts des zu testenden Temperaturbereichs.
Wenn Sie beispielsweise die Temperatur zwischen 25 und 85 Grad testen möchten, wählen Sie für die drei Punkte 25, 55 und 85 Grad aus.
2. Berechnen Sie den Temperaturkoeffizienten des Steinhart-Hart-Modus Der Steinhart-Hart-Temperaturkoeffizient des Thermistors kann den Wert von A, B, C über die obigen 3 Temperaturpunkte berechnen.
Wenn Sie hier direkt die Werte der Temperatur koeffizienten A, B und C eingeben, zeigt die Temperaturkurve die neue Kurve direkt basierend auf den von Ihnen eingegebenen Werten A, B und C an, wobei die Werte von ignoriert werden über drei Punkten.
3. Berechnen Sie den Temperatur koeffizienten des B-Werts Der B-Wert wird basierend auf den obigen Angaben (R1, T1) und (T2, R2) berechnet.
Wenn Sie hier den B-Wert eingeben, zeichnet die Kurve die R-T-Kurve direkt basierend auf dem B-Wert und ignoriert sie
NTC2 ist eine kostenlose Software zur Berechnung des Thermistorwiderstands.
Geben Sie den Widerstandswert von 25 Grad und den Wert B ein, um den entsprechenden Widerstandswert zu berechnen.
Das Ergebnis kann auch als Datei gespeichert werden.
Dies ist das beste Hilfsmittel zur Berechnung des Widerstandswerts.
Freunde, die es benötigen, können es von dieser Website herunterladen
NTC Calc Sheet 20150706.xlsx
Anleitung
Geben Sie den Widerstandswert und den Wert von 25 Grad ein, stellen Sie den Schritt zur Berechnung des Widerstandswerts bei jeder Temperatur ein und das Ergebnis kann als Datei exportiert werden.
Berechnungsformel für die NTC-Thermistortemperatur
Rt = R * EXP (B * (1 / T1 - 1 / T2)) Hier beziehen sich T1 und T2 auf K Grad, dh Kelvin-Temperatur, K Grad = 273,15 (absolute Temperatur) + Grad Celsius, wobei T2 = (273,15 + 25) Rt ist der Widerstandswert des Thermistors bei der Temperatur T1; R ist der Nennwiderstand des Thermistors bei normaler Temperatur T2; Der B-Wert ist ein wichtiger Parameter des Thermistors; e^ = EXP ist die n-te Potenz von e (der Eulerschen Zahl 2,71828182845904) Finden Sie T1 = ln (Rt / R) / B + 1 / T2
C-Programm:
#include "math.h" const float Rp=10000.0; //10K const float T2 = (273.15+25.0);;//T2 const float Bx = 3950.0;//B const float Ka = 273.15; float Get_Temp(void) { float Rt; float temp; Rt = Get_TempResistor(); //like this R=5000, T2=273.15+25,B=3470, RT=5000*EXP(3470*(1/T1-1/(273.15+25)), temp = Rt/Rp; temp = log(temp);//ln(Rt/Rp) temp/=Bx;//ln(Rt/Rp)/B temp+=(1/T2); temp = 1/(temp); temp-=Ka; return temp; }
Quelle:
https://www.ntcsensors.com/Thermistor_rechner_Datenblatt_PDF/
https://www.ntcsensors.com/NTC_Thermistor_Widerstands_rechner/
https://www.ntcsensors.com/Thermistorrechner_Datenblatt_pdf/
Der B-Wert ist der konstante Wert des NTC-Thermistors.
Das heißt, NTC-Thermistorchip (Halbleiterkeramik) nach Hochtemperatursintern, Bilden eines Materials mit negativem Temperaturkoeffizienten mit einem spezifischen Widerstand.
Unterschiedliche Formulierungen und Sintertemperaturen der Widerstandsbildung haben unterschiedliche B-Werte, sogenannte Materialkonstanten.
Oder als thermischer Index bezeichnet.
NTC-Thermistor, der B-Wert ist, wie man berechnet? Temperaturkoeffizient bezieht sich auf den Temperaturanstieg von 1 Grad, Widerstandsänderungsrate.
Konvertieren Sie den Wert von B in die Formel für den Widerstandstemperaturkoeffizienten:
Thermistortemperaturkoeffizient = B-Wert / T ^ 2 (T ist die absolute Temperatur des zu konvertierenden Punktes) Bei gleicher Temperatur ist der Widerstand umso kleiner, je größer der B-Wert ist. B-Wert Berechnungsformel: T1 / T2 ist in der Regel 25/85 oder 25/50 oder 25/100, abhängig von der Definition der verschiedenen Hersteller R1 = der Widerstandswert bei der Temperatur T1 R2 = Widerstand bei Temperatur T2 T1 = 298,15 K (273,15 + 25 ° C) ist als Kay-Temperatur definiert T2 = 358,15 K (273,15 + 85 ° C) ist als Kay-Temperatur definiert Widerstand bei Temperaturänderungen im wärmeempfindlichen Index,
Die Einheit ist K.
Dieser Parameter ähnelt der Steigung der RT-Kurve des NTC-Produkts.
Je größer der Wert, umso größer die Widerstandsänderung.
Quelle:
https://www.ntcsensors.com/Was_ist_der_B_Wert_des_NTC_Thermistors_/
https://wetec.vrok.de/rechner/cntcptc.htm
https://de.wikipedia.org/wiki/Steinhart-Hart-Gleichung
Quelle:
https://www.ahlborn.com/de_DE/temperaturmessung
Pt100, Pt1000, NTC, KTY und Ni1000 KennlinienDie Kennlinien der verschiedenen Messelemente können Sie aus der nachfolgenden Übersicht ersehen:
Quelle:
https://blog.beamex.com/de/temperatursensoren-kalibrieren-so-funktionierts
https://www.digikey.at/de/articles/how-to-accurately-sense-temperature-using-thermistors
0) Temperaturmessung mit Temperatursensoren / Temperaturfühler
Analog Digital Sensoren
Analog Ausgang : PT100 PT500 PT1000 LM34 LM35
Digital Ausgang : DHT11 DHT22 AM2302 TMP36 LM335 DS18B20 in Edelstahl
Digital Ausgang I2C, SPI, 1Wire : TMP101 LM75 DS1621 DS1821
PWM-Ausgang : MAX6673
Wenn man digitale Sensoren (-40 °C bis +125 °C +/-2 °C) verwendet ist alles einfacher und genauer !
ARDUINO UNO Temperatursensoren
Quelle:
300_ARDUINO-x_Der ARDUINO als Steuerzentrale - Einführung in Mikrocontroller - Arbeitsheft (56 Seiten)_1a.pdf
https://test-wetterstation.de/temperaturmessung-mit-dem-arduino Digitaler versus analoger Temperatursensor Was ist ein digitaler Temperatursensor und was sollten Sie wissen, wenn Sie einen digitalen Temperaturfühler einsetzen möchten?
In diesem Beitrag bekommen Sie einen ersten Überblick.
1) Analog versus digital Thermoelemente, Widerstandsthermometer, NTC und PTC liefern Ausgangssignale, die sich kontinuierlich mit der Temperatur ändern.
Wir nennen sie analoge Signale. Auch ein nachgeschalteter Messwertumformer, der das Ausgangssignal in ein normiertes Signal,
z.B. 0 bis 10 V, wandelt, liefert ein analoges Signal.
Ein digitaler Temperaturfühler ist ein Messfühler mit integriertem Analog-Digital-Wandler.
Er wandelt das analoge Signal in ein digitales Signal; der Messwert wird im einfachsten Fall über einen 1-Draht-Bus übertragen.
Aber auch komplexere Bus-Systeme, wie CANopen, Profibus oder USB können zum Einsatz kommen.
2) Vorteile digitaler Temperatursensoren Während analoge Temperaturfühler an der Messstelle lediglich mit dem eigentlichen Messelement bestückt sind, ist bei einem digitalen Temperaturfühler gleich noch die notwendige Elektronik integriert.
Wohl und Weh sind aber dicht beieinander.
Positiv Das Temperatursignal wird nach der AD-Wandlung nicht mehr durch äußere Effekte und Störungen beeinflusst
– das ist ein klarer Vorteil gegenüber dem empfindlichen Analogsignal.
3) Nachteile digitaler Temperatursensoren Negativ Durch die integrierte Elektronik wird der Temperaturbereich deutlich eingeschränkt:
Während ein Widerstandsthermometer, klug konstruiert, bis über +500°C an der Messstelle verträgt, ist bei digitalen Temperaturfühlern bei +80 bis +125°C die Grenze erreicht, denn die Elektronik verkraftet nicht mehr.
Außerdem sind die Preise für digitale Temperaturfühler deutlich höher als für klassische analoge Fühler.
4) Auswahlkriterien Neben dem Temperaturbereich spielt die Auflösung des Messwertes bei digitalen Fühlern eine große Rolle
– hier geht es darum, wie feinteilig der ursprüngliche analoge Wert als Digitalwert dargestellt wird.
Die Auflösung ist nicht zu verwechseln mit der ebenfalls sehr wichtigen Genauigkeit, die angibt, wie weit das Messergebnis vom physikalisch absoluten Ergebnis abweicht.
NTC = Heißleiter PTC = Kaltleiter
(Negative Temperature Coefficient) (Positive Temperature Coefficient) für hohe Temperaturen
https://de.wikipedia.org/wiki/Heißleiter https://de.wikipedia.org/wiki/Kaltleiter
NTC billig aber ungenau wegen der Unlinearität eigentlich nur für 25° +- 20 °C geeignet !
Quelle:
300_Sprut-x_Platinenherstellung - Platinentips - Layouterstellung - belichten, entwickeln, ätzen_1a.pdf
300_Sprut-x_Temperaturmessung mit NTC, PTC, PT100, Thermoelement § B511 AD590J AD592A_1a.pdf
300_Springer-x_Passive Bauelemente - Hering und Bressler - Linearisierung der Kennlinie (21 Seiten)_1a.pdf
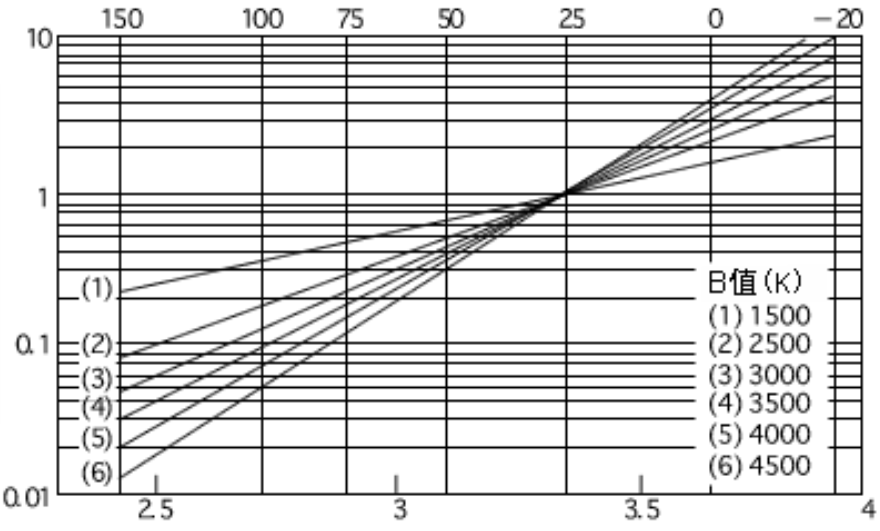
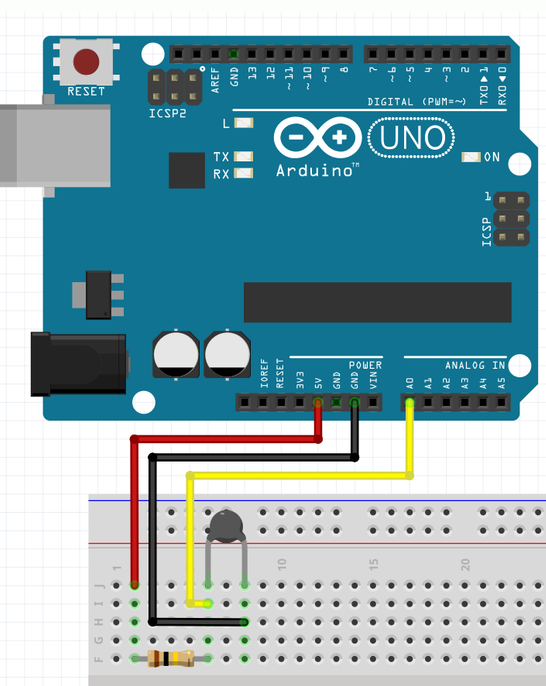
1) Unbekannten NTC Widerstand berechnen und messen!
B-Wert = NTC Thermistorkonstante berechnen z.B. B25/50= 3976K
NTC in 0 °C Eiswasser geben (nicht die Zuleitungen) Rn = 34.175 Ohm
NTC in 25 °C Wasser geben Rn = 10.010 Ohm
in Excel-Tabelle
300_c_fritz-x_Unbekannten NTC Widerstand berechnen und messen_1a.xls
die Werte eintragen !
Thermistorkonstante üblicherweise um B= 4000K
Berechnung der B-Werte für drei verschiedene Arten von Thermistoren
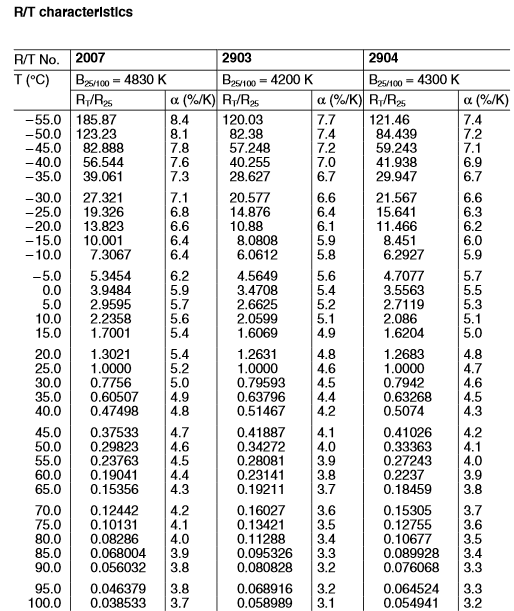
Thermistoreigenschaften von drei verschiedenen Typen von MMTL-Thermistoren sind in Tabelle 1 gezeigt.
Die Kennlinie eines Thermistors wird durch den Widerstand bei 25 °C (R25) und den Beta-Wert (B) definiert
Kennlinien als Temperaturkoeffizient (B25/50 oder B25/75 oder B25/85 oder B25/100).
Der B-Wert wird bestimmt durchfolgende Formel:
R: Widerstand bei absoluter Temperatur T (K)
R0: Widerstand bei absoluter Temperatur T0 (K)
B: B-Wert
T(K) = t(ºC) +273,15
Tabelle 1. Eigenschaften von drei verschiedenen Arten von Thermistoren basierend auf dem Beta-Wert B25/50
Quelle:
300_d_TI-x_Thermistor Selection Guide - TH1 TH2 TH3 - slua621_1a.pdfhttp://www.ti.com/lit/an/slua398/slua398.pdf https://www.ti.com/lit/an/slua398/slua398.pdf?ts=1636766039607
300_d_TDK-x_NTC Thermistor - General technical information - Formeln_1a.pdf
Dies ist notwendig bei unbeschrifteten / unbekannten NTC-Typen, für die kein Datenblatt vorhanden ist.
B-Wert = NTC Thermistorkonstante
Diese Formel wird zur Berechnung des B-Wertes verwendet.
R25 = R1ntc = 10,010k gemessener NTC-Widerstand bei Temperatur T1 von 25 °C
Rmes =R2ntc = 34,175k gemessener NTC-Widerstand bei Temperatur T2 von 0 °C
Excel-Formel
B-Werte sind üblicherweise um die 4000 K
ODER
NTC-Widerstand in Eiswürfelwasser = 0 °C und kochendes Wasser = 100 °C
Unbekannten B-Wert ermitteln: Sollte kein Datenblatt für den NTC vorhanden sein, kann man den B25/75 Wert (Thermistorkonstante) ermitteln, indem man den Widerstandswert des NTC bei zwei unterschiedlichen Temperaturen misst und diese Daten dann in obige Tabelle einträgt. Sollte der NTC beschriftet sein, kann man anstelle eines Messwertes auch den aufgedruckten Wert verwenden, z.B. 10k Ohm bei 25°. Je nach Temperaturbereich können unterschiedliche B-Werte ermittelt werden
z.B. B-Wert für 0 °C 25 °C 40 °C um eine höhere Genauigkeit zu erreichen.
Quelle:
http://www.afug-info.de
http://www.afug-info.de/Download/
http://www.afug-info.de/Download/tab/NTC/
Mit dieser Tabelle kann man Widerstands- und Temperaturwerte auch von unbekannten Typen berechnet lassen.
Die Ausgabe erfolgt als Liste und als Diagramm.
Zudem bietet sie die Möglichkeit unbekannte B-Werte (Thermistorkonstante) zu ermitteln sowie einen Konverter für Kelvin/Celsius/Fahrenheit (in beliebige Richtung)
und die Formeln.
Dieses Video zeigt die Funktionsweise von NTCs und wie man unbeschriftete und bekannte NTC-Widerstände messen und berechnen kann.
Mit kleiner Hilfe für Einsatz von Mikrocontroller (PIC, Atmel). NTCs (Thermistoren) können
u.a. als Temperaturfühler bzw. Temperatursensor, Temperatur-Schalter usw. eingesetzt werden.
NTC-Thermistor B-Wertformel.
Berechnungsformel für den NTC-Thermistorwiderstand:
EXP ODER e ^
R25 ODER R0
Rt = R25 * exp ( B * (T2-T1) / (T2*T1) )
Rt = R25 * exp ( B * (1/T1 - 1/T2 )
Rt = R25 * e ^ ( B * (1/T1 - 1/T2 )
R25 = 10k N TC R0 Nennwiderstand in Ohm bei 25 °C
e = 2,718281828459 Eulersche-Zahl
B25/75 = 4000K Exponentensteigung in Ohm
T1= 0 °C = 273,15K ist die aktuelle zu messende Temperatur in Kelvin Grad.
T2 = 25 °C = 298,15K ist die NTC Referenztemperatur bei 25 °C aber in Kelvin
Rt=10000*EXP(4000*(1/(273,15+0)-1/(273,15+25))) = 34140,6 Ohm bei 0 °C
Rt=10000*2,718281828459^(4000*(1/273,15-1/298,15)) = 34140,6 Ohm bei 0 °C
Rt=10000*2,718281828459^(4000*((273,15+25)-(273,15+0))/((273,15+25)*(273,15+0))) = 34140,6 Ohm bei 0 °C
T1= 40 °C = 313,15K
T2 = 25 °C = 298,15K Rt=10000*2,718281828459^(4000*(1/313,15-1/298,15)) = 5259,1 = Ohm bei 40 °C
R25 = 10000 Ohm
Rmess = 10000 Ohm
B25/75 = 4000K B-Wert od. beta
NTC Rechner zur ermittlung des B-Wertes - Afug-info.de - NTC_1a.ods
Quelle:
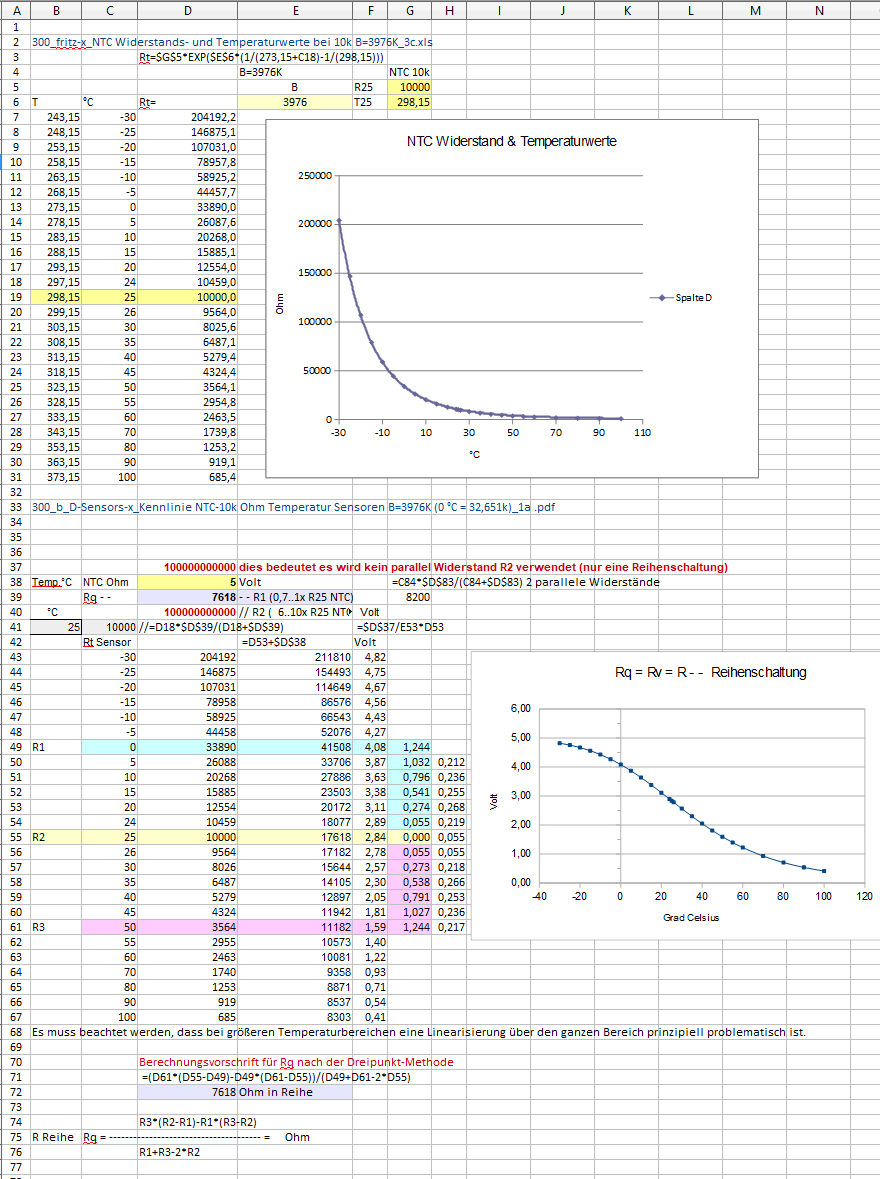
300_c_fritz-x_NTC Widerstand berechnen und Ausgangsspannung erhalten_1b.xls
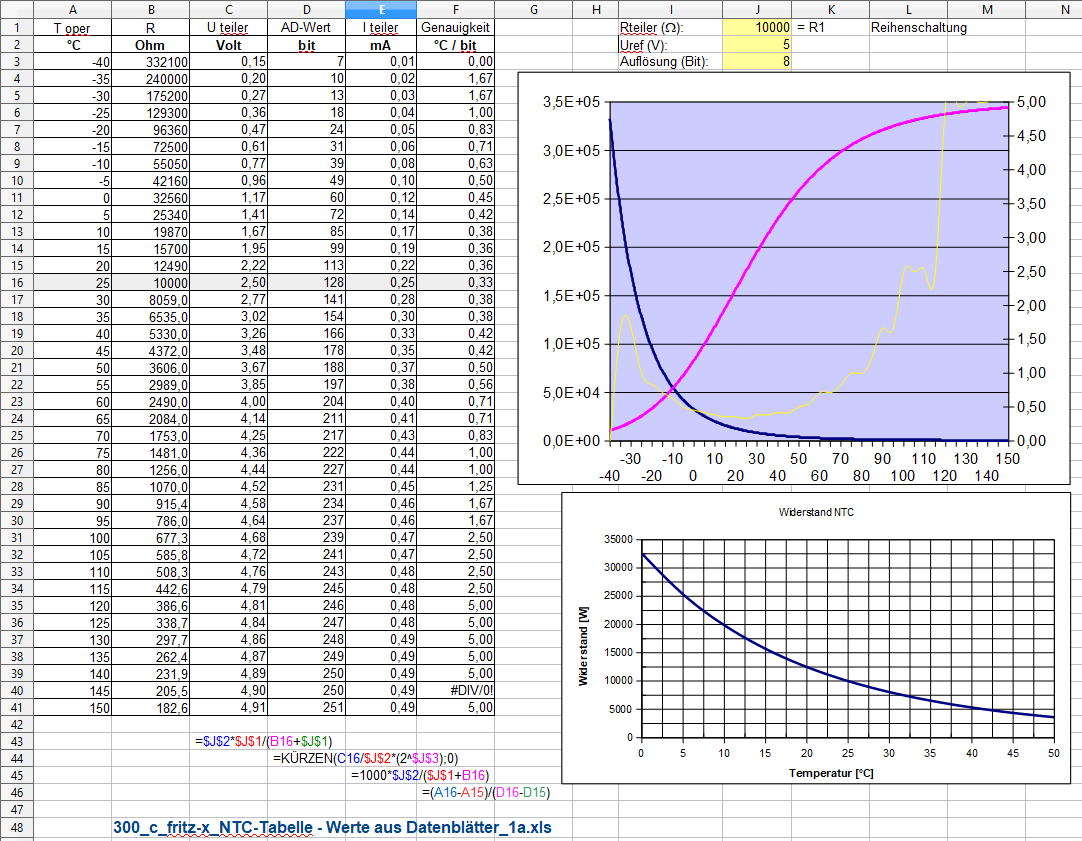
Die Tabelle gibt die Temperaturwerte von -50 bis +125 Grad Celsius mit den zugehörigen Widerstandswerten des NTC aus
- als Tabelle und Diagramm
- und beinhaltet zudem einen Rechner, um unbekannte Thermistorkonstanten (B-Wert) zu ermitteln.
Da in der Physik meist mit Kelvin gerechnet wird, rundet ein Temperatur-Konverter für Celsius, Fahrenheit und Kelvin die Tabelle ab.
Die Formeln für alle drei Rechner sind auf einem weiteren Tabellenblatt vermerkt.
Für die Programmierung von Microcontrollern wird zusätzlich der AD-Wert (8-bit und 10-bit) ausgegeben.
Alle Werte werden für normale und reverse Beschaltung angezeigt.
Nach dieser Methode - wie UNTEN zu sehen - zwischen 0 und 50 °C weitgehend linear !!!
Quelle:
NTC.ods
300_c_fritz-x_Unbekannten NTC Widerstand berechnen und messen_1a.xls
Download-Link Tabelle:
http://www.afug-info.de/Download/
http://www.afug-info.de/Download/tab/NTC/
www.Afug-Info.de
********************************************************I*
Koeffizienten-Version A, B, C, D - A1, B1, C1, D1
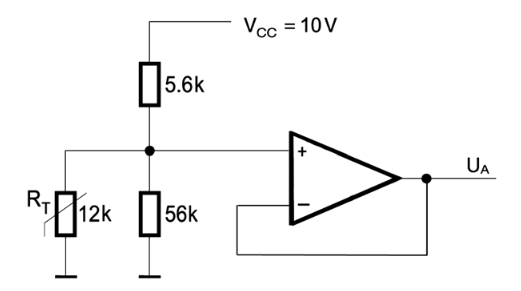
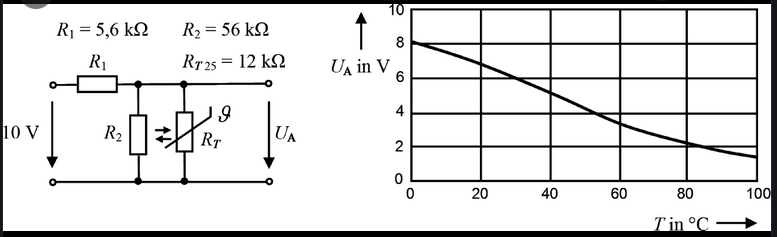
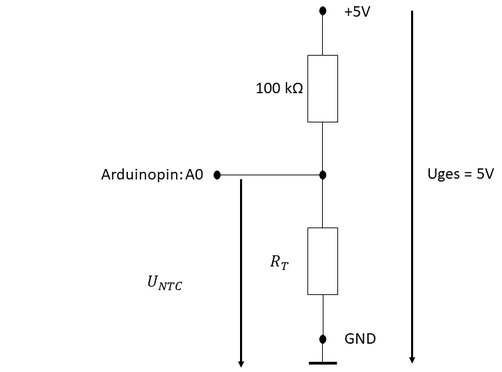
Einige Hersteller geben in ihren Datenblättern Koeffizienten für die Extended-Steinhart-Hart-Formel an. Gegeben sei eine Spannungsteilerschaltung aus dem Festwiderstand R1 gegen Vplus (plus) und dem NTC R2 gegen Vagnd (minus).
Varef kann gleich Vplus sein, kann aber auch abweichend angegeben werden.
Ein schneller Microcontroller könnte nun aus den Koeffizienten die Temperatur direkt in Fließkomma berechnen, oft braucht man jedoch nur wenige diskrete Werte die man besser einer Lookuptable entnehmen kann.
Daten der Schaltung
Die Extended Steinhart-Hart-Formel dient zum Berechnen des NTC-Widerstandswerts bei einer bestimmten Temperatur. 1/T=A1+B1*ln(R)+C1*ln2(R)+D1*ln3(R) T=1/( A1 + (B1*LN(R)) + (C1*(LN(R)^2)) + (D1*(LN(R)^3)) )
bzw. für den Widerstand
R(t)=R25 * exp(A+B/t+C/t2+D/t3) R25 ist dabei der Widerstand bei 25°C.
Einzelwerte
Einzelwert T(R)
Einzelwert R(T)
Einzelwert T(AD)
Tabellen
bei 25 °C R25 = 10000 Ohm
Tabelle für Grad-Stufen
Quelle:
http://www.loosweb.de/calculator/en/ntc_adc_v.html
http://www.loosweb.de/calculator/de/index.html
http://www.loosweb.de/calculator/de/notes.html
http://www.loosweb.de/calculator/de/uteiler.html
http://www.loosweb.de/calculator/de/muteiler.html
http://www.loosweb.de/calculator/de/cmin-linear.html
http://www.loosweb.de/calculator/de/lc_res.html
http://www.loosweb.de/calculator/de/linedrop.html
http://www.loosweb.de/calculator/en/uteiler.html
http://www.loosweb.de/calculator/de/cmin-sps.html
http://www.loosweb.de/calculator/de/bmax.html
http://www.loosweb.de/calculator/de/rc-snubber.html
http://www.loosweb.de/calculator/en/muteiler.html
http://www.loosweb.de/calculator/en/notes.html
http://www.loosweb.de/calculator/en/cmin-linear.html
http://www.loosweb.de/calculator/en/linedrop.html
********************************************************I*
1.3) Calculate the Resistance of an NTC at different Temperatures
Berechnen Sie den Widerstand eines NTC bei verschiedenen Temperaturen
Widerstand - Spannung Untc - Strom ntc - Leistung ntc - Erwärmung ntc
=LN(B1/B2) * ((A1+273,15) * (A2+273,15)) / ((A2+273,15) – (A1+273,15))
Quelle:
NTC Calc Sheet 20150706.ods
NTC Calc Sheet 20150706.xlsx
********************************************************I*
A) Standard NTC-Formel
T=B*Tn / (B+log (Rt/Rn)*Tn)
Wenn man die Daten des NTC hat dann kann man auch die Standardgleichung nehmen.
Steinhart-Hart macht vor allem Sinn, wenn man die Kennlinie des NTC erst selbst ermitteln muß.
B) Steinhart-Hart-Gleichung
Quelle:
https://de.wikipedia.org/wiki/Steinhart-Hart-Gleichung
https://en.wikipedia.org/wiki/Steinhart-Hart_equation
Berechnungsformel für den NTC-Thermistorwiderstand:
Rt = R25 * e ^ (B * (1/T1 - 1/T2)
R25 = 10k NTC
e = 2,718281828459 Eulersche-Zahl
B(25/75) = 4000K
T1= 125 °C = 398,15K
T2 = 25 °C = 298,15K
Rt=10000*2,718281828459^(4000*(1/398,15-1/298,15)) = 344,0 Ohm bei 125 °C
2) Steinhart and Hart Calculator
|
| 25 | 10000 | T1 / R1 | obere °C |
| 0 | 34141 | T2 / R2 | untere °C |
| B= | 4000 | K |
|
Der NTC-Thermistorwiderstand ist mit der Temperatur in Grad Kelvin durch die folgende Formel verbunden:
Wir können den NTC-Widerstand bei einer bestimmten Temperatur mit der Umkehrung der obigen Gleichung berechnen:
Beta ist wie folgt definiert:
Um R2 zu berechnen, können Sie diese Formel verwenden:
Ebenso können wir eine Temperatur für einen gemessenen Widerstand berechnen:
Alpha kann aus Beta wie folgt angenähert werden:
Alpha= -B/T2 *100
Delta(R)= [(1+Delta(RT25))/100)*(1+Delta(B)/100) - 1]*100 (%)
Dabei steht Delta für die Toleranz in %.
Wenn wir das Delta(R) bei einer bestimmten Temperatur kennen, können wir Alpha (TCR, der Temperaturkoeffizient) verwenden, um die Temperaturabweichung herauszufinden:Delta(T)= Delta(R) / min(Alpha).
https://daycounter.com/Calculators/Steinhart-Hart-Thermistor-Calculator.phtml
4a) Steinhart-Hart-Thermistor Calculator
Steinhart-Hart-Thermistor-Rechner
Steinhart-Hart Temperaturrechner
Der Thermistorwiderstand ist mit der Temperatur in Grad Kelvin durch die folgende Formel verbunden:
1/T= A + B*ln(R/Rt) + C*ln(R/Rt) 2 + D*ln(R/Rt) 3
In der Standard-Steinhart-Hart-Gleichung wird der C-Parameter auf Null gesetzt.Einige Hersteller verwenden jedoch alle 4 Koeffizienten. Im folgenden Rechner können Sie festlegen,
Ziehen Sie 273,15 ab, um Kelvin in Celsius umzurechnen.
Wenn das Ergebnis nicht 25C beträgt, liegt ein Problem mit den Koeffizienten vor.
Konstanten für die Berechnung der Temperatur aus NTC-Widerstand
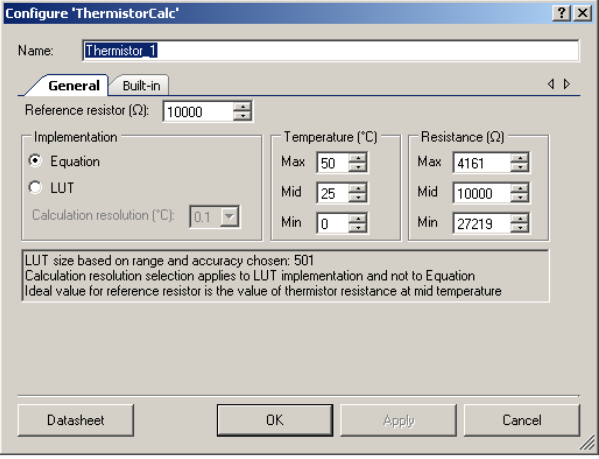
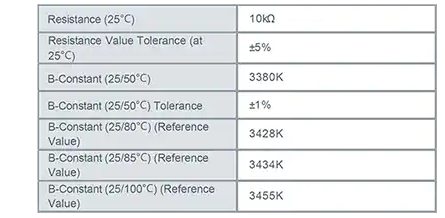
B25 = 3977K
Rref = 2200 Ohm
A=3.354016E-03 0.003354016
B=2.569850E-04 0.0002569850
C=2.61013E-06 0.00000262013
D=6.38309e-08 0.0000000638309
R = Widerstand des NTC bei Meßtemperatur
Viele Hersteller vernachlässigen es, diese Parameter in ein Datenblatt aufzunehmen, und müssen daher durch Lösen von 3 gleichzeitigen Gleichungen berechnet werden.
Je enger der Temperaturbereich ist, desto höher ist die Genauigkeit.
Beachten Sie, dass die Gleichung für einzelne Thermistoren, deren ABC-Koeffizienten individuell bestimmt werden, extrem genau ist.
Bei einer Gruppe von Thermistoren kann die resultierende Temperatur jedoch aufgrund von Abweichungen in der Charge abweichen.
Das Datenblatt sollte die Toleranz in %C angeben.
R= Rt*exp (A1 +B1 /T+C1 /T 2 + D1 /T 3 )
wobei exp die Umkehrung von ln im natürlichen Logarithmus ist.
Beachten Sie, dass sich die Werte für A 1 , B 1 , C 1 , D 1 von den Koeffizienten für die obige Gleichung unterscheiden!
Dieser Rechner berechnet einen Widerstand.Beachten Sie, dass Sie wählen können, ob Sie den dritten Begriff verwenden möchten oder nicht, indem Sie das Kontrollkästchen aktivieren.
B25 = 3977K
Rref = 2200 Ohm
A1=3.354016E-03 0.003354016
B1=2.569850E-04 0.0002569850
C1=2.61013E-06 0.00000262013
D1=6.38309e-08 0.0000000638309
R = Widerstand des NTC bei Meßtemperatur
R= Rt*exp (A1 +B1 /T+C1 /T 2 + D1 /T 3 )
Rt =10000*EXP(A1+B1/(273,15+25)+C1/(273,15+25)^2+D1/(273,15+25)^3) = 10k 25°C ergibt 10k Widerstand
Es ist ratsam, eine schnelle Überprüfung durchzuführen, indem Sie die Koeffizienten und 25 ° C
für die Temperatur eingeben, der resultierende Widerstand sollte nahe bei Rt liegen.
Die meisten Hersteller geben Alpha und Beta sowie die R-Toleranz bei Umgebungstemperatur an.
Beta ist temperaturabhängig und wird zwischen zwei Temperaturpunkten angegeben und kann verwendet werden,
Beispielsweise wird ein Beta zwischen 25 und 85 oft als B 25/85 bezeichnet.
Alpha der Temperaturkoeffizient wird auf Datenblättern oft als TCR bezeichnet.
Alpha ist für NTC-Thermistoren negativ und für PTC-Thermistoren positiv.
Beta ist wie folgt definiert:
B T1/T2 = 1/(1/T 1 -1/T 2 )ln(R 1 /R 2 ) (Kelvin)
Um R2 zu berechnen, können Sie diese Formel verwenden:
R2 = R1 / (exp( B*(1/ T1 - 1/ T2) ))
| 50 | 3603 | T1 / R1 | obere °C |
| 25 | 10000 | T2 / R2 | untere °C |
| B= | 3934 | K |
|
Ebenso können wir eine Temperatur für einen gemessenen Widerstand berechnen:
T 2 = T 1 *B/ln(R 1 /R 2 ) / (B/ln(R 1 /R 2 ) - T 1 ),
Beachten Sie, dass T Einheiten von Kelvin hat.
| 50 | 3603 | T1 / R1 | obere °C |
| 0 | 32650 | T2 / R2 | untere °C |
| B= | 3891 | K |
|
Thermische Zeitkonstante
Die thermische Zeitkonstante ist ein Maß dafür, wie schnell sich der Thermistor an Temperaturänderungen anpassen kann.
Wenn Sie schnelle Temperaturänderungen messen möchten, ist eine kleine Zeitkonstante wichtig.
Temperaturabweichung
Angesichts der Vielzahl von Parametern auf einem Datenblatt kann es eine Herausforderung sein, die Endgenauigkeit einer Thermistorfamilie zu kennen.
Die erste Berechnung ist die Gesamtwiderstandsabweichung:
Delta(R)= [(1+Delta(R T25 ))/100)*(1+Delta(B)/100) - 1]*100 (%)
Dabei steht Delta für die Toleranz in %.
Wenn wir das Delta (R) bei einer bestimmten Temperatur kennen, können wir Alpha (TCR, der Temperaturkoeffizient) verwenden, um die Temperaturabweichung zu berechnen:
Delta(T) = Delta(R)/min(Alpha).
Beachten Sie, dass Alpha umgekehrt proportional zur Temperatur ist.Wir erhalten also die maximale Abweichung, wenn Alpha bei der höchsten Temperatur im Bereich ausgewählt wird.
Aus der obigen Gleichung können wir Alpha von B bei einer gegebenen Temperatur abschätzen.
********************************************************I*
Um sie zu verwenden, müssen wir lernen, wie man aus dem gemessenen Widerstand einen Temperaturwert berechnet.
4b) Temperaturmessung mit NTC Thermistoren
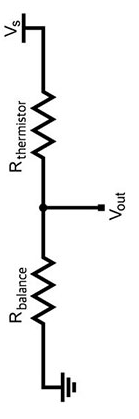
Im letzten Tutorial haben wir uns verschiedene Arten von Thermistoren und ihre Einsatzmöglichkeiten angesehen.In diesem Tutorial werden wir uns ansehen, wie man mit einem NTC-Thermistor einen Temperaturwert ermitteln kann.
Der erste Schritt besteht darin, den Widerstand des Thermistors zu messen.
Dies kann mit einer einfachen Spannungsteilerschaltung wie der unten gezeigten erfolgen.
Die Spannung kann dann mit dem ADC eines Mikrocontrollers gemessen
Zu Testzwecken kann auch ein Multimeter zur Widerstandsmessung verwendet werden.
Sobald wir den Widerstand des NTC gemessen haben, können wir mit der Berechnung des Temperaturwertes fortfahren.
Bevor wir uns die Formeln ansehen, ist es wichtig zu verstehen, dass sie alle die Temperatur in Kelvin (K) verwenden.
Die Steinhart-Hart-Gleichung wurde ursprünglich für Temperaturmessungen in der Ozeanographie entwickelt und 1968 erstmals veröffentlicht.
Hier ist sie:
1/T = A0 + A1(lnR) + A2(lnR)^2 + A3(lnR)^3
T = Temperatur in Kelvin (Kelvin = Celsius + 273.15)
A0, A1, A3 = aus Thermistormessungen abgeleitete Konstanten
R = Widerstand des Thermistors in Ohm
ln = Natural Log (Log zur Napierian-Basis 2.718281828...) Die drei Koeffizienten
 ,
,  und
und  werden als Steinhart-Hart-Koeffizienten bezeichnet und sind für verschiedene, handelsübliche Typen von Heißleiterwiderständen in deren technischen Datenblättern tabelliert.
werden als Steinhart-Hart-Koeffizienten bezeichnet und sind für verschiedene, handelsübliche Typen von Heißleiterwiderständen in deren technischen Datenblättern tabelliert.
B1 = 4.777517E+03 4777,517
B2 = -1.201468E+05 -120146,8
B3 = -2.168775E+06 -2168775
Die Gleichung enthält noch ein quadratisches Glied, welcher aber öfters weggelassen wird, da angeblich vernachlässigbar klein.
Bei unbekannten Steinhart–Hart-Koeffizienten lassen sie sich durch Messungen von drei, über den Messbereich verteilten Punkten, ermitteln.
Die drei Koeffizienten a, b, und c werden normalerweise im Datenblatt angegeben.
Hat man die drei Koeffizienten für seinen NTC-Thermistor gefunden, kann man mit der Gleichung die Temperatur für den gemessenen Widerstand berechnen.
Es muss nur noch der Temperaturwert von Kelvin in Grad Celsius umgerechnet werden.
Die Grafik zeigt ein Beispiel für die R-T-Kennlinie eines NTC-Thermistors.
Für praktische Anwendungen haben nur die Terme mit den Koeffizienten A0 A1 A3 eine Bedeutung, die restlichen Koeffizienten sind in Relation so klein, dass sie für praktische Anwendungen im Bereich der Messtechnik im Messbereich um 0 °C bis +70 °C vernachlässigt werden können.[2]
Damit reduziert sich die Steinhart-Hart-Gleichung für praktische Anwendungen auf die vereinfachte Form:
Die drei Koeffizienten A0 A1 A3 werden als Steinhart-Hart-Koeffizienten bezeichnet und sind für verschiedene, handelsübliche Typen von Heißleiterwiderständen in deren technischen Datenblättern tabelliert.[3] Bei unbekannten Steinhart–Hart-Koeffizienten lassen sie sich durch Messungen von drei, über den Messbereich verteilten Punkten, ermitteln.
>> R1 = 74400
R1 = 74400
>> T2 = 408.15
T2 = 408.15
>> R2 = 428.8
R2 = 428.80
>> T3 = 572.5
T3 = 572.50
>> R3 = 37.7249
R3 = 37.725
1, log(R2), log(R2) ^ 3;
1, log(R3), log(R3) ^ 3 ]
A =
1.0000 11.2172 1411.4149
1.0000 6.0610 222.6542
1.0000 3.6303 47.8448
>> b = [ 1/T1; 1/T2; 1/T3 ]
b =
0.0039502
0.0024501
0.0017467
ans =
6.9835e-004
2.8865e-004
9.9147e-009
A = 6.9835E-04 0,00069835
B = 2.8865E-04 0,00028865
Das ist eine ziemlich komplexe Gleichung, die mehrere Parameter (A, B, C) erfordert, die wir normalerweise nicht für den normalen NTC haben.
1. Vorbereitungen: zuvor ist zu messen:
R_lowest bei T_lowest
R_middle bei T_middle
R_highest bei T_highest
R_current bei gesuchter Temperatur (in °C)
float Divisor;
float edTl, edTm, edTh;
float lnRm, lnRh;
float ln3Rm, ln3Rh;
float Ergebnis;
float lgR;
float R_current;
edTl = 1/(Temp_lowest + 273.15);
edTm = 1/(Temp_middle + 273.15);
edTh = 1/(Temp_highest + 273.15);
lnRm = log(R_middle);
ln3Rm = lnRm*lnRm*lnRm;
lnRh = log(R_high);
ln3Rh = lnRh*lnRh*lnRh;
Divisor = lnRm*ln3Rh - lnRh*ln3Rm;
AA = 1/(Temp_lowest + 273.15);
BB = ((edTm - edTl)*ln3Rh - (edTh - edTl)*ln3Rm) / Divisor;
CC = ((edTh - edTl)*lnRm - (edTm - edTl)*lnRh) / Divisor;
2. die Temperaturberechnung
lgR = log(R_current/R_lowest);
Ergebnis = 1.0/(AA + BB*lgR + CC*lgR*lgR*lgR) - 273.15; // in °Celsius
https://www.mikrocontroller.net/topic/210255
Geben Sie drei Datensätze gemäß den tatsächlichen Daten
A = 0,7016010760E-03 0,0007016010760
B = 2,880146315E-04 0,0002880146315
C = 0,126859E-07 0,0000000126859
C2 = 2,880146315E-04 0,0002880146315
A) B-Parameter-Gleichung
Die B-Parameter-Gleichung kann auf NTC-Sensoren (Heißleiter), d.h. RTD-Elemente mit negativem Koeffizienten k, angewendet werden.

Dabei gibt der Koeffizienten RT0 den Widerstand bei der Temperatur T0 an, der B-Parameter kann den Angaben des Sensorherstellers entnommen oder durch Messung des Widerstandes bei zwei bekannten Temperaturen bestimmt werden.
Zur Berechnung des B-Parameters kann folgende Beispieldatei (Download: ZIP) verwendet werden.
300_b_Beckhoff-x_B-Parameter-Gleichung - Berechnung - EL3204-0200_1a.xls
Die IEC 751 bzw. die deutsche Übersetzung DIN EN 60751 definiert die elektrischen Eigenschaften von Platin-Temperatursensoren.

Der Parameter R0 gibt den Widerstand in Ohm des Platinsensors bei T=0°C an.
Die in der Norm definierten Parameter A, B und C sind bereits im CoE Verzeichnis 0x8003:yy hinterlegt.
Steinhart-Hart-Gleichung
Die Steinhart-Hart Gleichung kann auf NTC-Sensoren (Heißleiter), d.h. RTD-Elemente mit negativem Koeffizienten k, angewendet werden.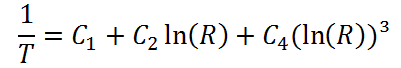
Die Koeffizienten C1, C2 und C4 können entweder direkt den Herstellerdaten entnommen, oder aber berechnet werden.
Zur Berechnung der Steinhart-Hart Parameter steht eine Beispieldatei (Download: ZIP) zur Verfügung.
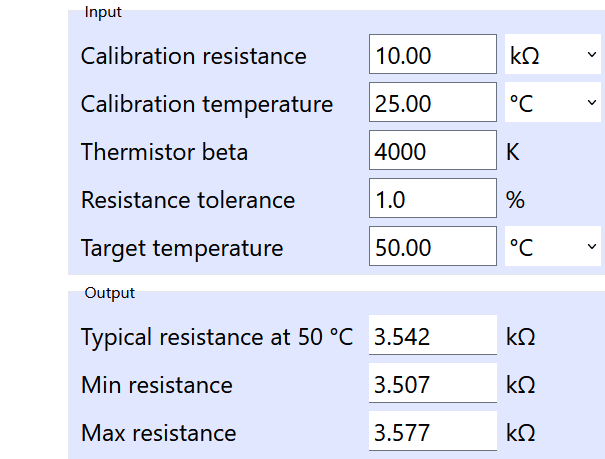
Sensoreigenschaften: NTC 10kΩ +/- 1% bei 25°C, Beta B25/75=3435.
Quelle:
Parameter B = 0,000233
Parameter C = 0 (kann auch 0 sein da Zahl immer sehr klein und unbedeutend)
Wenn beide Parameter bekannt sind, können wir die folgende Formel verwenden, um den gemessenen Widerstandswert in eine Temperatur umzurechnen:
Wir können auch den Widerstand für eine gegebene Temperatur berechnen:
Die nachstehende Grafik zeigt eine R-T Kennlinie, wie sie mithilfe der Beta-Gleichung berechnet werden kann.
Die Beta-Formel ist eigentlich eine vereinfachte Version der Steinhart-Hart-Gleichung, die den letzten Korrekturterm wegfallen lässt.Dies habe ich für die Beispielwerte getan, die in der Grafik für die Steinhart-Hart-Gleichung verwendet werden.
Ein häufiges Problem bei vielen Arduino-Kits oder Sensor-Packs ist, dass es keine Datenblätter gibt.
Der erste Schritt besteht darin, den Nennwert bei 25 °C zu bestimmen.
Um die Zwei-Punkt-Kalibrierung durchzuführen, benötigen wir einen zweiten Widerstandswert für eine bekannte Temperatur.
Anhand beider Kalibrierpunkte können wir schließlich den Betawert B25/100 berechnen:
T0 und R0 sind die Werte unseres ersten Kalibrierungspunktes.R ist der gemessene Widerstand bei 100 °C (T=273,15 + 100 = 373,15K).
Zum Schluss wollen wir uns noch mit der Linearität befassen.
Wir können die Linearität zulasten der Empfindlichkeit verbessern, indem wir den Wert von R2 anpassen.
Wenn wir eine gute Linearität im Bereich von 0 °C bis 50 °C wollen, berechnen wir den Wert für 25 °C (T = 298,15 K):
Im Falle eines anderen Mittelpunktes müssen wir zuerst die Beta-Formel anwenden, um den erwarteten Widerstand Rt zu berechnen.
https://devxplained.eu/de/blog/widerstandskombinationen
https://devxplained.eu/de/blog/spannungsteiler
https://devxplained.eu/de/blog/potentiometer
https://devxplained.eu/de/blog/widerstandsmessung
https://devxplained.eu/de/blog/thermistoren
https://devxplained.eu/de/blog/analoge-temperaturmodule
https://devxplained.eu/de/blog/temperaturschwellwertmodul
https://devxplained.eu/de/blog/halbleiter
********************************************************I*
5) Thermistor Calculator LabJack Corporation (1A)
Berechnungsformel für den NTC-Thermistorwiderstand: Rt = R25 * EXP (B * (1/T1 - 1/T2)
1/T= A + B*ln(R) + C*ln(R)^2 + D*ln(R)^3
Daumenregel: bei der Zieltemperatur
(wenn es ein Bereich ist: in der Mitte des Temperaturbereichs)
sollten NTC und Vorwiderstand etwa den gleichen Widerstand haben.
Also bei 10k NTC bei 25° eben 10k (8k)
Ub=2,5V
R25 NTC = 10k
R2 = 1k, 10k 100k
Us=2,5/(A21+1000)*1000
Volts LJTR-1k = 2,5 * 1000 / (A21+1000)= 0.227273
Volts LJTR-10k = 2,5 * 10000 / (A21+10000) = 1.250000
Volts LJTR-100k = 2,5 * 100000 / (A21+100000) = 2.272727
| 25 | 10000 | T1 / R1 |
| 0 | 32650 | T2 / R2 |
|
|
B= | 3854,57 |
| °K | Ohm NTC | = LN(B1/B2) * ((A1+273,15) * (A2+273,15)) / ((A2+273,15) - (A1+273,15)) |
300_b_Calc-x_Diagramme mit OpenOffice.org Calc erstellen_1a.pdf
300_b_Calc-x_OpenOffice.org Kapitel 8 - Die Verwendung von Grafiken in Calc (16 Seiten)_1a.pdf
********************************************************I*
6) Steinhart-Hart Temperature Calculator
Steinhart-Hart-Thermistor-RechnerSteinhart-Hart Temperaturrechner
Der Thermistorwiderstand ist mit der Temperatur in Grad Kelvin durch die folgende Formel verbunden:
1/T= A + B*ln(R/Rt) + C*ln(R/Rt) 2 + D*ln(R/Rt) 3
In der Standard-Steinhart-Hart-Gleichung wird der C-Parameter auf Null gesetzt.
Ziehen Sie 273,15 ab, um Kelvin in Celsius umzurechnen.
Es ist ratsam, eine schnelle Überprüfung der Gesundheit durchzuführen, indem Sie die Koeffizienten und den gleichen Wert für Rt und R eingeben.
TDK 10k B57861S0103F045
0 °C 32650 Ohm
25 °C 10k
50 °C 3603 Ohm
Steinhart-Hart Temperaturrechner
Der Thermistorwiderstand ist mit der Temperatur in Grad Kelvin durch die folgende Formel verbunden:1/T= A + B*ln(R/Rt) + C*ln(R/Rt) 2 + D*ln(R/Rt) 3
In der Standard-Steinhart-Hart-Gleichung wird der C-Parameter auf Null gesetzt.
Einige Hersteller verwenden jedoch alle 4 Koeffizienten.
Im folgenden Rechner können Sie festlegen, ob dieser Begriff verwendet werden soll oder nicht, indem Sie ihn einfach auf Null setzen.
Ziehen Sie 273,15 ab, um Kelvin in Celsius umzurechnen.
Es ist ratsam, eine schnelle Überprüfung der Gesundheit durchzuführen, indem Sie die Koeffizienten und den gleichen Wert für Rt und R eingeben.
Wenn das Ergebnis nicht 25C beträgt, liegt ein Problem mit den Koeffizienten vor.
Viele Hersteller vernachlässigen es, diese Parameter in ein Datenblatt aufzunehmen, und müssen daher durch Lösen von 3 gleichzeitigen Gleichungen berechnet werden.
Beachten Sie, dass die Gleichung für einzelne Thermistoren, deren ABC-Koeffizienten individuell bestimmt werden, extrem genau ist.
Bei einer Gruppe von Thermistoren kann die resultierende Temperatur jedoch aufgrund von Abweichungen in der Charge abweichen.
Das Datenblatt sollte die Toleranz in %C angeben.
Quelle:
https://www.thinksrs.com/downloads/programs/therm%20calc/ntccalibrator/ntccalculator.html
https://labjack.com/sites/default/files/forums/2018-12-03%20%282%29.png
********************************************************I*
7) Diverse Calculators
NE555 - Impedanz - LM317 - Ohm - LED - LM3914 - LM3915 - Thermistor
Thermistor Resistance Calculator
Simple check to verify if the calculated resistance.
Thermistor versus Temperature Plot. V2
Enables the user to see the changes in Thermistor Resistance due Temperature.
555 Timer Calculator (Astable Mode)
Will give you the timing values for the 555 timer such as frequency and duty cycle calculator.
Capacitor Impedance Calculator
Calculate the impedance of a capacitor.
LM317 Calculator
Find the value of the voltage adjustment resistor required to set the output of an LM317.
Ohms Law Calculator
Calculate for current, voltage, resistance, and power.
Resistance Values Calculator
Simple check to verify if the calculated resistance.
LED Series Resistance Calculator
Determines the ideal series resistor value for powering LEDs
LM317 Regulator Calculator V2
Determines the Resistor value for a LM317 regulator
IC555 Type1 Astable Timer Calculator V1.0
Calculates the Frequency and Period of a 555 Type1 Astable Timer Circuit.
IC555 Type2 Astable Timer Calculator V1.0
Calculates the Frequency and Period of a 555 Type2 Astable 50/50 Mark/Space Timer Circuit.
IC555 Monostable Timer Calculator V1.0
Calculates the High Output Period of a 555 Monostable Timer Circuit.
LM3914 Calculator V2
Calculates the LM3914 Circuit Components.
LM3915 Calculator V2
Calculates the LM3915 Circuit Components.
Calculator for PSU's using Rectifier, Smoothing Capacitor and a Regulator. V2
Enables the User to see the effect of different component Values.
Quelle:
https://www.electro-tech-online.com/tools/
********************************************************I*
Silicon Labs Si7013 Relative Humidity and Temperature Sensor I2C driver.
8) Si7013 Thermistor Correction Calculator
Berechnungsformel für den NTC-Thermistorwiderstand: Rt = R25 * e ^ (B * (1/T1 - 1/T2)
Si7013-Thermistor-Correction-Calculator.xlsx
Si7013-Thermistor-Correction-Calculator.ods
Si7013-Thermistor-Correction-Calculator_1a.xls
Si7013-Thermistor-Correction-Calculator.xls
https://www.silabs.com/sensors/humidity/si7006-13-20-21-34/device.si7013-a20-gm1
https://silabs.com/public/miscellaneous
Si7013 Thermistor Correction Calculator Table
********************************************************I*
9) Steinhart and Hart Calculator
Steinhart and Hart Calculator - | MVWautotechniek.nl
NTC_karakteristiek-1 (schreibgeschützt)_1a.xls
********************************************************I*
10) NTC R/T Calculation 5.0 - Web-basierte Anwendung
Das neue Web-basierte Tool erlaubt die Berechnung der Widerstand-Temperatur-Beziehung von EPCOS NTC-Thermistoren.Kennlinien lassen sich durch Einstellen des Temperaturbereichs und der Widerstandstoleranz sowie durch Wählen der gewünschten Schrittweite individuell berechnen und gestalten.
Die Ergebnisse lassen sich als PDF ausdrucken oder zur Weiterverarbeitung in einer Tabellenkalkulation,
z.B. Excel, exportieren.
Die Datenbank des Tools umfasst das aktuelle Spektrum der EPCOS NTC-Thermistoren.
Was ist neu?
Über die Website haben Sie stets Zugriff auf die aktuelle Datenbank.
Bei der Produktauswahl ist nun ersichtlich, welche EPCOS Produkte sich nicht für neue Designs empfehlen.
Die Kennlinien lassen sich durch entsprechende Filterung individuell aufbereiten.
Die Daten können im csv (=comma separated values) Format zur Weiterverarbeitung in einer Tabellenkalkulation exportiert werden.
z.B. B57332V5103F360 1%
https://www.tdk-electronics.tdk.com/download/531152/71487ad65dd78f1844cf52efcee5836d/pdf-rt.pdf
https://www.tdk-electronics.tdk.com/web/designtool/ntc/
https://www.tdk-electronics.tdk.com/de/194578/design-support/tools-fuer-entwickler/ntc-thermistoren/ntc-r-t-calculation-5-0
https://www.tdk-electronics.tdk.com/download/531116/19643b7ea798d7c4670141a88cd993f9/pdf-general-technical-information.pdf
Enter Thermistor Datasheet Values.
Ein Thermistor ist ein elektronischer Temperaturfühler , der bei relativer Temperaturänderung eine Widerstandsänderung zeigt.
Der Name leitet sich von zwei anderen Wörtern ab, "thermischer Widerstand".
Für Temperaturmess- und Regelanwendungen werden im Allgemeinen Geräte mit negativem Temperaturkoeffizienten (NTC) verwendet.
Das „-t°“ im Schaltsymbol bezeichnet in der Regel ein NTC- Gerät.
Diese Komponenten sind sehr nützlich, um Projekte mit Mikrocontrollern zu verbinden.
Um dieses Gerät richtig zur Temperaturmessung zu verwenden, ist ein Potentialteiler- Netzwerk (PD) oft die ideale Schaltungsanordnung.
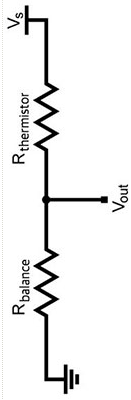
Mit steigender Temperatur steigt Vout
Potenzielle Teilerformel - Mit NTCTaschenrechner
R S :R T :
V ein :
V aus :
Mit steigender Temperatur sinkt Vout
Potenzielle Teilerformel - Mit NTC
Taschenrechner
NTC Temperatur zu Widerstand
Die Geräteleistung ist normalerweise ein Widerstandswert bei einer bestimmten Temperatur, z. B. 4,7 kΩ bei 25 °C.
Somit ist
Die Formel erfordert, dass alle Temperaturen in Kelvin (K) angegeben werden, daher müssen Sie 273,15 umrechnen.
Der Betakonstantenwert ß ist auch ein weiterer gerätespezifischer Parameter, der normalerweise in der Dokumentation des verwendeten Geräts zu finden ist.
NTC-Charts
Hersteller bieten oft eine für ihre NTC-Komponente spezifische Tabelle an, die den Widerstand bei verschiedenen Temperaturen zeigt.
Wenn Sie den Wert nicht berechnen können, kann ein Diagramm sehr nützlich sein.
Leider ist jedes Diagramm spezifisch für ein Gerät; Daher müssen Sie diese Informationen beim Hersteller einholen.
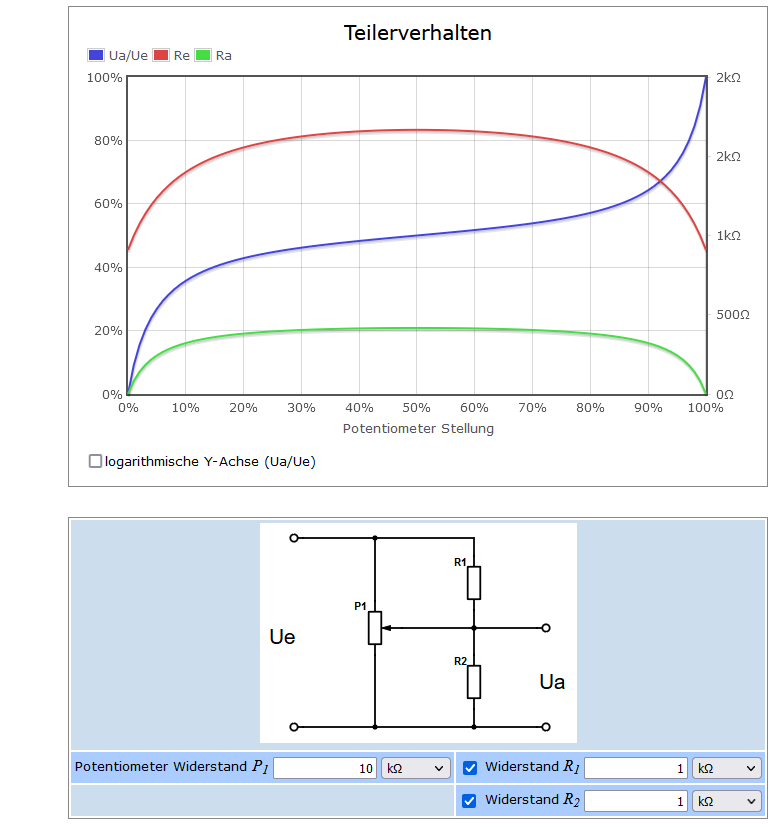
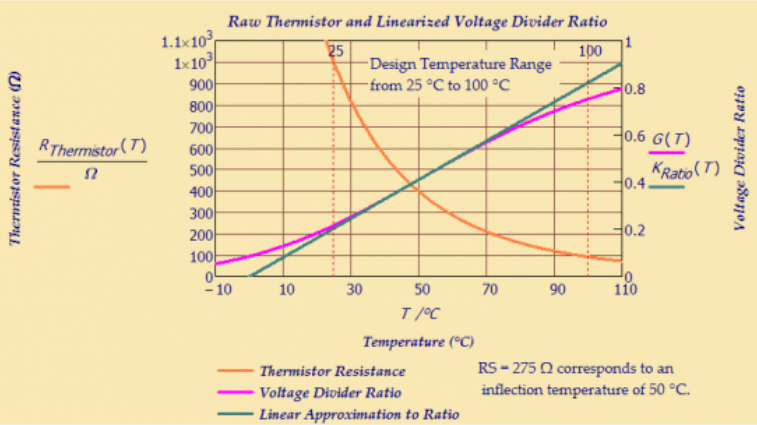
13a) Potenzialteiler mit NTC-Thermistor
Ein Thermistor ist ein temperaturempfindlicher Widerstand, dessen Widerstand sich in Abhängigkeit von der Temperatur ändert.Es verbindet als Teil eines Potentialteilers, auch Spannungsteiler genannt, ein Netzwerk in einen Stromkreis.
Von allen verschiedenen Arten von Temperaturfühlern ist der Thermistor der empfindlichste und liefert die größte Widerstandsänderung bei Temperaturänderungen.
Ein Nachteil dieses Gerätes besteht darin, dass seine Ausgangscharakteristik nichtlinear ist und der Steinhart-Hart-Kurve sehr nahe kommt.
Das Funktionsprinzip ist daher sehr einfach; sein Widerstand ändert sich bei Temperaturänderungen.
Dieser Artikel soll die Grundlagen und Prinzipien der Funktionsweise zeigen und könnte für Studenten auf GCSE- und Abschlussniveau nützlich sein.
NTC-Thermistor
Hier ist ein schematisches Symbol eines Thermistors mit negativem Temperaturkoeffizienten (NTC).Es gibt auch einen Thermistor mit positivem Temperaturkoeffizienten (PTC), der durch +t im Symbol gekennzeichnet ist.
Temperatursensor-IC
Integrierte Temperaturerfassungsschaltungen (IC) sind derzeit auf dem Markt erhältlich.
Ein Vorteil dieser Geräte besteht darin, dass ihre Ausgangscharakteristik linear ist.
Anwendungen
Seine Einsatzmöglichkeiten sind endlos und werden im Allgemeinen dort eingesetzt, wo ein Temperatursensor mit Temperaturregelungsfunktionen erforderlich ist.
- Zentrales Heizsystem
- Auto Motor
- Klimaanlage
- Waschmaschine
- Kühlschrank
- Raketensysteme
Schaltkreis
Hier ist eine Schaltung eines Potentialteilers mit einem NTC-Thermistor.Beispiel 1:
Bei einer Temperatur von 100 °C beträgt der Ausgang 6,0V.
In der obigen Schaltung beträgt bei R1 = 1000 Ohm und Vs = 10V die Ausgangsspannung des Spannungsteilers 9,1V bei einer Temperatur von 25 °C.
Bei einer Temperatur von 100 °C beträgt der Ausgang 4,0 V.
Daher sinkt in dieser Schaltung die Ausgangsspannung mit steigender Temperatur.
Widerstandsrechner
Hinweis:
Alle Temperaturen sollten in °C angegeben werden, da der Rechner die Umrechnung in Kelvin automatisch vornimmt.
Normalerweise messen wir den Widerstand des Thermistors bei jedem Temperaturgrad durch ein Laborexperiment, wie unten auf dieser Seite gezeigt.
Es gibt auch eine Gleichung zur Berechnung des Widerstandswerts bei jeder gegebenen Temperatur; es gibt jedoch einen ungefähren Wert für eine bestimmte Komponente.
Gleichung
Die Parameter der Gleichung sind sehr einfach. RT ist der gesuchte Widerstandswert bei der Temperatur T.
RT0 ist der Widerstand bei der Temperatur T0.
Dies ist typischerweise der im Datenblatt angegebene Widerstand bei 25 °C.
Im Allgemeinen ist eine Beta-Berechnung nicht erforderlich, da sie im Datenblatt des Herstellers für eine bestimmte Komponente leicht verfügbar ist.
T und T0 sind Temperaturen in Kelvin. Die folgende Formel rechnet Celsius in Kelvin um.
Kelvin = Celsius + 273,15
Wenn das Datenblatt beispielsweise einen Thermistor mit einem Widerstand von 10 kΩ bei 25 °C angibt, dann gilt RT0 = 10000 Ω und T0 = 298,15.
Thermistor-Experiment
Das Testen eines Thermistors ist einfach, da Sie nur ein digitales Messgerät benötigen, um seinen Widerstand zu messen.Verwenden Sie dann einen Fön, um heiße Luft darüber zu blasen, um die Temperatur zu erhöhen.
In einem Labor ist es normalerweise genauer, das Bauteil in eine nicht leitende Flüssigkeit zu tauchen, die sich langsam erwärmt.
Da sich das Thermometer in dieser Flüssigkeit befindet, sind die Messwerte genauer.
Graph
Um ein solches Experiment durchzuführen, benötigt man ein digitales Messgerät, um den Widerstand zu messen.
Kurve
Aus der Kurve können Sie sehen, dass mit steigender Temperatur der Widerstand abnimmt.
Berechnungsformel für den NTC-Thermistorwiderstand: Rt = R25 * e ^ (B * (1/T1 - 1/T2)
Widerstandstabelle
| Temperatur (°C) | Thermistorwiderstand (Ω) |
| 0 | 32553 |
| 5 | 25319 |
| 10 | 19843 |
| fünfzehn | 15666 |
| 20 | 12456 |
| 25 | 9970 |
| 30 | 8032 |
| 35 | 6510 |
| 40 | 5309 |
| 45 | 4354 |
| 50 | 3590 |
| 55 | 2976 |
| 60 | 2479 |
| 65 | 2076 |
| 70 | 1746 |
| 75 | 1476 |
| 80 | 1252 |
| 85 | 1066 |
| 90 | 914 |
| 95 | 785 |
| 100 | 674 |
Die obige Tabelle zeigt die Versuchsergebnisse, die auf einer Anwendung vom Typ "OpenOffice" aufgetragen werden.
********************************************************I*
Die fortschrittlichen Batteriemanagement-ICs mit Tankanzeige von TI verwenden ein Polynommodell,
1. Einleitung
Der Firmware-Algorithmus in den Batteriemanagement-ICs der erweiterten Tankanzeige von TI verwendet ein Polynommodell, um Übersetzen Sie die an den Thermistoranschlüssen gemessene Spannung in Temperatur.
Der Thermistor-Koeffizienten-Rechner ist eine Microsoft Excel-Tabelle, die als ZIP-Datei in der gleiche Ort wie dieser Bericht.
2. Betriebstheorie
Solver, ein Add-In-Tool für Excel, das zur Standardinstallation gehört, wird in diesem Fall verwendet, um ein Lösung einer Menge von Polynomen 3. Ordnung.
Die Aufgabe von Solver besteht darin, den Wert in Zelle B33 (siehe Abbildung 1) zu minimieren, der die Summe der Normen für jeden ist bekannten Datenpunkt.
4 Schaltungsänderungen
Für maximale Genauigkeit sollte die Spannungseingangsspannung zum A/D-Wandler in der Tankanzeige begrenzt werden auf etwa 82% der Referenzspannung, die in diesem Fall gleich Vcc ist.
Die empfohlene Thermistorschaltung mit R1 = 8,45k Ohm, R2 = 61,9k Ohm und Thermistor = 10k Ohm bei 25 °C, sollte die obige Anforderung in den meisten Fällen erfüllen.
********************************************************I*
Guide To Choosing Resistance Values
- R1 is the resistance in ohms at t1 (°K)
- R2 is the resistance in ohms at t2 (°K)
-
ß is the temperature constant
- Deg K = Deg C + 273
- e = 2.7184
********************************************************I*
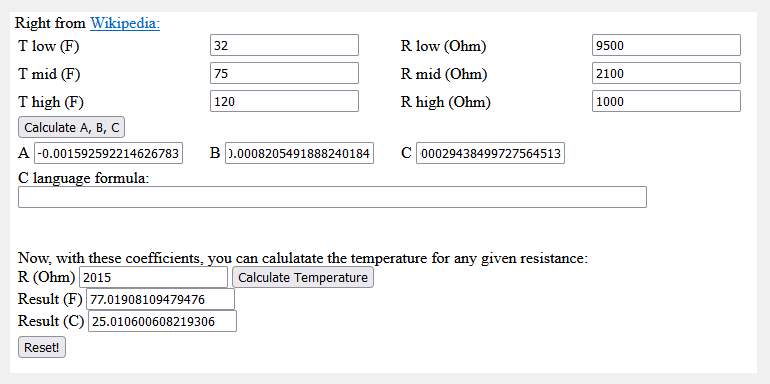
21a) Calculating Temperature from Resistance A B C D
≤ 0.01 °C error for 50 °C temperature spans within the range of temperatures (t) -80 °C ≤ t ≤ 0 °C.
≤ 0.01 °C error for 100 °C temperature spans within the range of temperatures (t) 0 °C ≤ t ≤ 260 °C.
≤ 0.02 °C error for 100 °C temperature spans within the range of temperatures (t) -80 °C ≤ t ≤ 25 °C.
Eine der wichtigsten Eigenschaften des NTC-Thermistors ist seine Fähigkeit, seinen Widerstand in Abhängigkeit von seiner Körpertemperatur wiederholt und vorhersehbar zu ändern.
Es gibt 4 grundlegende Möglichkeiten, wie die NTC-Thermistorindustrie die R/T-Kurveneigenschaften eines NTC-Thermistors definiert:
Die Steinhart-Hart-Gleichung bietet eine hervorragende Kurvenanpassung für bestimmte Temperaturspannen im Temperaturbereich von -80 °C bis 260 °C.
Während es in der Industrie üblich war, den ln(R)^2 Term der Gleichung zu eliminieren, glauben wir bei North Star Sensors auf der Grundlage veröffentlichter Studien, dass diese Praxis auf einer zu starken Vereinfachung der Stein-Hart-Hart-Gleichung beruht und sollte nur in relativ engen Temperaturbereichen verwendet werden.
Um die A-, B-, C- und D-Koeffizienten für einen bestimmten Temperaturbereich zu bestimmen, wird der Widerstand eines NTC-Thermistors unter Nullleistungsbedingungen an vier Temperaturpunkten gemessen, wobei T1 die niedrigste Temperatur des Bereichs ist, T2 und T3 sind die mittleren Temperaturen, und T4 ist die höchste Temperatur des Bereichs.
Es ist wichtig zu beachten, dass Widerstände und Temperaturen für diesen Rechner auf bestimmte NTC-Kurven beschränkt sind .
Bei der Verwendung der Steinhart-Hart-Gleichung müssen bestimmte Vorkehrungen getroffen werden, damit der Benutzer die gewünschte Genauigkeit und Unsicherheit der zu berechnenden Widerstands-Temperatur-Daten erreicht.
≤ 0,001 °C Fehler für 50 °C Temperaturspanne im Temperaturbereich (t) 0 °C ≤ t ≤ 260°C.
≤ 0,01 °C Fehler für 50 °C Temperaturspanne im Temperaturbereich (t) -80 °C ≤ t ≤ 0 °C.
≤ 0,01 °C Fehler für 100 °C Temperaturspanne im Temperaturbereich (t ) 0 °C ≤ t ≤ 260 °C.
≤ 0,02 °C Fehler für 100 °C Temperaturspanne im Temperaturbereich (t) -80 °C ≤ t ≤ 25 °C.
Wenn eine Anwendung eine Kurvenanpassung mit höchstmöglicher Genauigkeit über eine Temperaturspanne von mehr als 50 °C oder 100 °C erfordert, kann die gewünschte Temperaturspanne zur Berechnung von A, B . in 50 °C-Schritte oder 100 °C-Schritte zerlegt werden , C, D-Koeffizienten und Widerstands-Temperatur-Daten.
Die spezifischen A-, B-, C- und D-Koeffizienten eines Thermistors hängen sowohl von der NTC-Thermistorkurve als auch vom R25 dieses Thermistors ab.
North Star Sensoren bieten sechs RT-Kurven zur Auswahl.
Kurve 44
1 °C Rt / R25 Tabelle (.pdf) R/T Spezifikationen (.pdf) Ω vs. °C Rechner (.xlsx)
Als eines der vielseitigsten und am weitesten verbreiteten Materialien ist es in einer Vielzahl von physikalischen Konfigurationen erhältlich, einschließlich Standardspitzen-ODs, Mini-ODs und Mikro-ODs.
Im Allgemeinen fallen die R25-Werte für Kurve 44 in den Bereich von 1 kΩ bis 100 kΩ.
Zum Beispiel hat Kurve 44 einen NTC-Wert von -4,4 %/̊C
Kurve 35
1 °C Rt / R25 Tabelle (.pdf) R/T Spezifikationen (.pdf) Ω vs. °C Rechner (.xlsx)
R25-Werte für Kurve 35 liegen typischerweise im Bereich von 50 Ω bis 500 Ω, was für Tieftemperaturmessungen nützlich ist.
Kurve 38
1 °C Rt / R25 Tabelle (.pdf) R/T Spezifikationen (.pdf) Ω vs. °C Rechner (.xlsx)
R25-Werte für Kurve 38 liegen typischerweise im Bereich von 100 Ω bis 1,5 kΩ, was wie Kurve 35 für Tieftemperaturmessungen nützlich ist.
Kurve 40
1 °C Rt / R25 Tabelle (.pdf) R/T Spezifikationen (.pdf) Ω vs. °C Rechner (.xlsx)
Der Curve 40 10k Ω Thermistor wird in bestimmten Branchen häufig verwendet. R25-Werte sind im Bereich von 5 kΩ bis 50 kΩ erhältlich
Kurve 43
1 °C Rt / R25 Tabelle (.pdf) R/T Spezifikationen (.pdf) Ω vs. °C Rechner (.xlsx)
Die Kurve 43 wird verwendet, wo ein kleiner Thermistor mit hohem Widerstand erwünscht ist. Typischerweise fallen die R25-Werte für Kurve 43 in den Bereich von 20 kΩ bis 50 kΩ, sie können jedoch auch mit einem Wert von nur 5 kΩ angeboten werden.
Kurve 47
1 °C Rt / R25 Tabelle (.pdf) R/T Spezifikationen (.pdf) Ω vs. °C Rechner (.xlsx)
Mit R25-Werten von bis zu 150 kΩ kann die Kurve 47 ideal für [batteriebetriebene] Anwendungen mit geringem Stromverbrauch sein. R25-Werte reichen von 10 kΩ bis 150 kΩ.
R ist der Widerstand in Ohm (Ω)
A, B, C und D sind Koeffizienten, die von der Kurve, dem Temperaturbereich und dem Widerstand bei 25 °C abhängen
North Star Sensors hat R/R25-Verhältnistabellen für jedes seiner Thermistormaterialien veröffentlicht.
Für gängige R25-Werte werden auch 1 °CR/T-Tabellen veröffentlicht.
Bitte kontaktieren Sie North Star Sensors, wenn Sie zusätzliche Informationen oder R/T-Spezifikationen benötigen.
Beta (β)
Der Beta-Wert (β) eines Thermistors ist ein Indikator für die Steigung der Widerstands-Temperatur-Kurve und wird berechnet, indem die Widerstandswerte des Geräts unter Nullleistungsbedingungen an zwei Temperaturpunkten gemessen werden, typischerweise bei 0 °C und 50 °C.Der β-Wert ist keine echte Materialkonstante und temperaturabhängig.
Hier sind verschiedene Temperaturbereiche für β-Werte der Kurven von North Star Sensors:
Widerstand-Temperatur-Verhältnis
Die Hersteller von NTC-Thermistoren definieren ihre verschiedenen R/T-Materialien auch, indem sie Widerstandsverhältnisse und Verhältnistoleranzen für R0/R50, R0/R70 und R25/R125 veröffentlichen, wobei „Rt“ der Nullleistungswiderstand bei der entsprechenden Temperatur in Grad Celsius ist.
Hier sind verschiedene Verhältniswerte der R/T-Kurven von North Star Sensors:
Negativer Temperaturkoeffizient [NTC]
Der Temperaturkoeffizient des Widerstands oder Alpha (∝) eines Thermistors ist definiert als das Verhältnis der Widerstandsänderungsrate mit der Temperatur zum Widerstand des Thermistors bei einer bestimmten Temperatur (T), wie durch den folgenden Ausdruck gezeigt:
Der Alpha-Wert wird verwendet, um den Temperaturkoeffizienten eines NTC-Thermistors an einem Temperaturpunkt zu berechnen.
Bei NTC-Thermistoren wird der Alpha- oder Temperaturkoeffizient in Einheiten von minus Prozent Widerstandsänderung pro Grad Celsius ausgedrückt.
North Star Sensors verwendet den NTC bei R25 für jedes seiner R/T-Kurvenmaterialien in seiner grundlegenden Thermistor-Teilenummer, um den Querverweis seiner Thermistorprodukte auf die Industriestandardkurven zu erleichtern.
Da der NTC für jeden Temperaturpunkt entlang der R/T-Kurve unterschiedlich ist, werden austauschbare NTC-Thermistoren mit einer Temperaturtoleranz anstatt einer Widerstandstoleranz über einen Temperaturbereich spezifiziert [dh ± 0,2 °C von 0 °C bis 100 °C] .
NTC (%/°C) × Temperaturtoleranz (± °C) = ± % Widerstandstoleranz
Um beispielsweise die Widerstandstoleranz eines Curve 44-Thermistors mit einer Toleranz von ± 0,2 ̊C bei 100 ̊C zu bestimmen,
Hier sind die NTC-Werte bei 25 °C für die R/T-Kurven von North Star Sensors: Zum Beispiel hat Kurve 44 einen NTC-Wert von -4,385 %/̊C
Die 1 °C-Tabellen für die NTC-Werte für jede Kurve bei jeder Temperatur neben den Widerstandsverhältniswerten finden Sie auf der folgenden Seite:
Quelle:
Temperaturkurven von North Star Sensoren********************************************************I*
Adrien RICCIARDI
255 3.300000 0.000000 -273.********************************************************I*
Ich weiß, dieses Thema findet sich überall im Web, aber die Berechnungen werden manchmal etwas kryptisch dargestellt, als wollte der Autor so viele verschachtelte Berechnungen in eine Zeile bringen, also wollte ich nur etwas schreiben, das es Schritt für Schritt erklärt , insbesondere wenn es um die eigentlichen Berechnungen geht.
Der Arduino hat mehrere ADC-Ports, mit denen wir eine Spannung oder besser einen "ADC-Wert" lesen können.
Wenn die Temperatur sinkt, erhöht sich der Wert des Widerstands und damit auch der Messwert am Analogport.
Angenommen, wir haben einen 10k Ohm Serienwiderstand und einen NTC, den wir vorerst 'R' nennen.
Dann ist die in der Mitte messbare Spannung
Vo=R / (R+10K) * Vcc
Die analogPort-Messwerte liefern jedoch keine Spannung, sondern einen ADC-Wert, der leicht berechnet werden kann
ADC-Wert = Vo * 1023/Vcc // wenn zum Beispiel Vo = 4 Volt der ADC = 818
oder
ADC-Wert = 1023 * (Vo / Vcc )
Wenn wir nun die beiden Formeln kombinieren oder Vo in der Formel für ADC 'ersetzen', erhalten wir Folgendes:
ADC-Wert = (R/(R+10K))*Vcc*1023/Vcc
Wie wir mit Vcc multiplizieren, aber auch durch Vcc dividieren können wir das aus der Gleichung herausnehmen und erhalten
ADC-Wert = (R / (R + 10k)) * 1023
ADC-Wert = 1023 * R / (10 + R),
wenn wir den Wert von erhalten möchten R aus dieser Gleichung wird
R=10k / (1023 / ADC-1)
Wenn das etwas zu schnell geht, hier ist die Gleichung ausgearbeitet.
Ich bevorzuge Bilder gegenüber den 'in-line'-Formeln, da einige Leute Probleme haben, die PEMDAS / BODMAS- Operationsreihenfolge zu verstehen .
Dies wird zur Subtraktion von R Work -R in die MultiplikationDa wir an R interessiert sind, dividieren Sie beide Seiten durch den eingeschlossenen Bruch
Die '10' stand für '10k' und da wir nicht immer eine 10k Ohm verwenden, machen wir es nur allgemeiner :
Also, solange wir den Wert des Vorwiderstandes kennen, können wir den Wert des NTC aus dem gemessenen ADC-Wert berechnen.
Denken Sie daran, dies gilt für eine Pull-up-Konfiguration.
Wenn es sich um eine Pull-Down-Konfiguration handelt, ist die Berechnung des ADC-zu-Widerstandswerts umgekehrt.
Rntc = R-Serie *(1023/ADC-1); // für Pulldown
Rntc = R-Serie /(1023/ADC – 1)); // für Pull-Up-Konfiguration
Wie würde das in einem Programm / sketch aussehen?
//Measure NTC valuebyte NTCPin = A0;const int SERIESRESISTOR = 10000;void setup(){ Serial.begin(9600);}void loop(){ float ADCvalue; float Resistance; ADCvalue = analogRead(NTCPin); Serial.print("Analog value "); Serial.print(ADCvalue); Serial.print(" = ");//convert value to resistance Resistance = (1023 / ADCvalue) - 1; Resistance = SERIESRESISTOR / Resistance; Serial.print(Resistance); Serial.println(" Ohm"); delay(1000);}//end programDen Widerstand des NTC zu kennen ist schön, aber es sagt uns nicht viel über die Temperatur aus… oder doch?
Nun, viele NTCs haben einen Nennwert, der bei 25 Grad Celsius gemessen wird.
Wenn Sie also einen 10k-NTC haben und ihn auf 10k messen, bedeutet dies, dass er in diesem Moment 25 Grad beträgt.
Das hilft dir nicht viel, wenn die Messung anders ist.
Du könntest eine Tabelle führen, in der jeder Widerstandswert für eine Temperatur steht.
Diese Tabellen sind sehr genau, erfordern jedoch viel Arbeit und Speicherplatz.
Es gibt jedoch eine Formel, die Steinhart-Hart-Gleichung , die eine gute Annäherung an die Umrechnung von Widerstandswerten eines NTC in Temperatur liefert.
Es ist nicht so genau wie die Thermistortabelle (schließlich ist es eine Annäherung), aber es ist ziemlich genau.
Die Steinhart-Hart-Gleichung sieht so aus:
Das ist eine ziemlich komplexe Gleichung, die mehrere Parameter (A, B, C) erfordert, die wir normalerweise nicht für den normalen NTC haben.
Das sieht so aus:
B- oder β- Parametergleichung
NTC-Thermistoren können auch mit der Parametergleichung B25/75 (oder β ) charakterisiert werden,
die im Wesentlichen die Steinhart-Hart-Gleichung mit ist
,
und
,
wobei die Temperaturen in Kelvin angegeben sind und R0 der Widerstand bei der Temperatur T0 (25 °C = 298,15 K) ist. Auflösen nach R ergibt
oder alternativ,
wo .
Dies kann für die Temperatur gelöst werden:
To ist die Nenntemperatur, 25 °C in Kelvin (= 298,15K).
Ro ist der Nennwiderstand des NTC (also bei 25 Grad).
Wir müssen nur R (den gemessenen Widerstand) einstecken , um T (Temperatur in Kelvin) zu erhalten, die wir dann in °C umrechnen.
Das Programm sieht wie folgt aus:
//---------------byte NTCPin = A0;#define SERIESRESISTOR 10000#define NOMINAL_RESISTANCE 10000#define NOMINAL_TEMPERATURE 25#define BCOEFFICIENT 3950void setup(){Serial.begin(9600);}void loop(){float ADCvalue;float Resistance;ADCvalue = analogRead(NTCPin);Serial.print("Analog value ");Serial.print(ADCvalue);Serial.print(" = ");//convert value to resistanceResistance = (1023 / ADCvalue) - 1;Resistance = SERIESRESISTOR / Resistance;Serial.print(Resistance);Serial.println(" Ohm");float steinhart;steinhart = Resistance / NOMINAL_RESISTANCE; // (R/Ro)steinhart = log(steinhart); // ln(R/Ro)steinhart /= BCOEFFICIENT; // 1/B * ln(R/Ro)steinhart += 1.0 / (NOMINAL_TEMPERATURE + 273.15); // + (1/To)steinhart = 1.0 / steinhart; // Invertsteinhart -= 273.15; // convert to CSerial.print("Temperature ");Serial.print(steinhart);Serial.println(" oC");delay(1000);}//-------------Dies ist natürlich
kein ideales Programm.Es ist immer gut, ein paar Proben zu nehmen und sie zu mitteln.
Die folgende Funktion kann das für Sie tun:
float sample(byte z)/* This function will read the Pin 'z' 5 times and take an average. */{ byte i; float sval = 0; for (i = 0; i < 5; i++) { sval = sval + analogRead(z);// sensor on analog pin 'z' } sval = sval / 5.0; // average return sval;}
Float-Sample (Byte z)/* Diese Funktion liest den Pin 'z' 5 Mal und nimmt einen Durchschnitt. */{ Byte i; Schwimmerwert = 0; für (i = 0; i < 5; i++) { sval = sval + analogRead (z); // Sensor am analogen Pin 'z' } sval = sval / 5.0; // Durchschnitt Rückgabewert;}Die Speisung des Vorwiderstands und des NTC aus der 5-Volt-Versorgung des Arduino ist möglich.
Die Arduino-Stromleitung hat jedoch Störungen.
Für genaue Messungen ist es besser, die 3,3 Volt-Leitung als analoge Referenz zu verwenden und den Widerstand von dort zu speisen.
fügen Sie dazu den folgenden Code in das Setup ein
// connect AREF to 3.3V and use that as VCC for the resistor and NTC!
analogReference(EXTERNAL);
https://www.mikrocontroller.net/topic/210255
https://de.wikipedia.org/wiki/Steinhart-Hart-Gleichung
24) Präzise Temperaturmessung mit 12bit-ADC und NTC
NTC 100k, 0,5%, B25/75 4250K
an einem Spannungsteiler mit R2=100k (0,05%, 10ppm)
Quelle:
https://www.mikrocontroller.net/topic/508494
********************************************************I*
25) NTC als Spannungsteiler linearisieren?
Rs = 0,7 .. 1x R25 NTC
Rp = 6 .. 10x R25 NTC
Die, in diesem Arbeitsblatt vorgestellte Variante der Linearisierung hat den Vorteil, dass die Minimal- und Maximalwerte eines Temperaturbereiches mit ausreichender Praxisgenauigkeit linearisiert werden.
Allerdings muss beachtet werden, dass bei größeren Temperaturbereichen eine Linearisierung über den ganzen Bereich prinzipiell problematisch ist.
Einige Werte für die Eingabemaske müssen aus dem Datenblatt des ausgewählten NTC-Widerstandes übernommen werden.
In diesem Beispiel liegt der NTC auf Massepotenzial, mit dem Vorteil, dass sich Störeinflüsse über das Sensorkabel leichter wegfiltern lassen.
Die Änderung der Größe der Ausgangsspannung Vm erfolgt in diesem Beispiel umgekehrt zur Änderung der Temperatur.
Die Spannung Vm muss hochohmig ausgekoppelt werden, damit niederohmige Nachfolgestufen keine Verfälschungen dieses Signals vornehmen.
Quelle:
https://www.electronicdeveloper.de/MesstechnikNTCLinearR.aspx
NTC-47k.plt
https://www.mikrocontroller.net/topic/393997
https://www.mikrocontroller.net/topic/87295
https://www.mikrocontroller.net/topic/324816
https://www.mikrocontroller.net/topic/189467
https://www.mikrocontroller.net/topic/106939
300_d_fritz-x_Temperatursensoren, Temperaturmessung mit NTC, PTC, Thermoelemente, Strahlungsthermometer_1a.pdf
********************************************************I*
26) NTC-Thermistor Parameter - B Wert Beschreibung & Berechnungsmethode
TAG: NTCThermistorTemperatursensor pt100Kfz-SensorenWassertemperatur sensorThermische BeständigkeitPTC-SensorNTC-SensorPTC-ThermistorTemperatursensor10K 3950 thermistorThermoelement-Sensor
Die Hauptparameter des Thermistors:
Der B-Wert ist der Wärmekoeffizient des Thermistors mit negativem Temperaturkoeffizienten.
Das heißt, der Thermistorchip (eine Halbleiterkeramik) bildet nach dem Hochtemperatur Sintern ein Material mit einem spezifischen spezifischen Widerstand.
Der B-Wert kann berechnet werden, indem der Widerstand bei 25 Grad Celsius und 50 Grad Celsius (oder 85 Grad Celsius) gemessen wird.
Der Temperaturkoeffizient bezieht sich auf die Temperatur für jede Erhöhung um 1 Grad.
Widerstand Temperaturkoeffizient = B-Wert / T ^ 2 (T ist der absolute umzurechnende Temperaturwert).
NTC-Thermistor B-Wertformel.
Berechnungsformel für den NTC-Thermistorwiderstand: Rt = R * EXP (B * (1 / T1-1 / T2)
In 1 ist Rt der Thermistor im T1-Temperaturwiderstand;
In 2 ist R der Nennwiderstand des Thermistors bei T2-Umgebungstemperatur;
3, B-Wert ist ein wichtiger Parameter des Thermistors;
4, EXP ist die n-te Potenz von e;
5, wobei sich T1 und T2 auf die K-Grad-Kelvin-Temperatur beziehen, K = 273,15 (absolute Temperatur) + Grad Celsius;
3, B-Wert ist ein wichtiger Parameter des Thermistors laut Datenblatt meist < 4000K.
4, EXP ist die n-te Potenz von e der Eulerschen-Zahl von 2,718281828459.
Rt = 5000 * EXP (3435 (1 / t - 1 / 298,15))
Rt = 5000 * EXP (3950 (1 / T - 1 / 298,15))
Unter der Annahme, dass die beiden NTC-Widerstände den gleichen Widerstand haben,
3435 (1 / t - 0,003354) = 3950 (1 / T - 0,003354)
NTC-Widerstandswert von 3950 B auf 3435 Temperaturwertumwandlungsalgorithmus:
T = 3950 / (3435 / t + 1,727) = 3950 t / (1,727 t + 3435)
Unter ihnen:
NTC-Widerstandswert von 3950 B auf 3435 Temperaturwertumwandlungsalgorithmus:
T = 3435 / (3950 / T-1,727) = 3435T / (3950-1,727T)
Darunter:
Die elektronischen Produktparameter von Yaxun lauten wie folgt:
MF5A-502F-3470 Modelle des Thermistors
Epoxidgehäuse vom Typ MF5A 502
F - Die Toleranz beträgt (Genauigkeit) ± 1%
Rt = 5000 * EXP (3470 * (1 / T1 + 0 / (273,15 + 25)) bei 0 °C
********************************************************I*
Steinhart-Hart Thermistor Calibration in Excel Using Matrix Formulas
27) Steinhart-Hart-Thermistorkalibrierung in Excel mit Matrixformel
Originaltitel:
ExampleThermistor.xlsx
https://www.mathscinotes.com/2019/11/steinhart-hart-thermistor-calibration-in-excel-using-matrix-formulas/
https://www.mathscinotes.com/2011/07/thermistor-mathematics/
https://en.wikipedia.org/wiki/Thermistor#Steinhart-Hart_equation
https://www.mouser.com/datasheet/2/600/Ametherm_09182017_DG103395-1214847.pdf
https://de.scribd.com/document/467599348/ExampleThermistor-xlsx
********************************************************I*
28) NTC-Berechnung (1A)
Berechnungsformel für den NTC-Thermistorwiderstand:
R25 = 298,15K (298,15K- 273,15K = 25 °C)
T = 293,15 - 273,15 = 20 °C
Rt=Rn*e^(B/Tu-B/Tn)
Tu: Aktuelle Temperatur (Umgebungstemperatur / in der Regel Raumtemperatur)
Tn=298,15 Tn ist die NTC Referenztemperatur bei 25 °C aber in Kelvin
R20: Widerstand bei 293,15K
B: 4000K
Rt = 10000 * 2,718281828459 ^ [ 4000 * (1/Tu - 1/298,15) ]
273,15 -30 °C = 243,15
273,15 = 0,00 °C
298,15 K - 273,15 = 25,00 °C
Sensorkennlinien
B-Werte bei B(25/50) =3950K (mittlere Wert zwischen 25 und 50°C)
B-Werte bei B(25/100)=3996K (mittlere Wert zwischen 25 und 100°C)
Temperatur immer in Kelvin (es gibt keine minus Grade)
R25= 10k 0hm bei 25 °C
Rt = R25 * e ^ (B * (1/T - 1/T25))
Rt=10000*EXP(3976*(1/273,15-1/298,15)) = 33890,0 bei 0°C
Rt=10000*EXP(3976*(1/(273,15+50) - 1/298,15)) = 3564,1 bei 50°C
B = ln(R/R25)/(1/T-1/T25)
B = LN (33890,0/10000) / (1/273,15-1/298,15) = 3976,0
B = LN (3564,1/10000) / (1/(273,15+50) - 1/298,15) = 3976,0
NEU
300_fritz-x_NTC Widerstands- und Temperaturwerte bei 10k (B=3976K)_3c.xls
Quelle:
300_NTB-x_Linearisierung von resistiven Sensoren - NTC Temperatursensoren_1a.pdf
300_fritz-x_NTC Widerstands- und Temperaturwerte bei 10k_1c.xls
Spalten markieren > MENU > Einfügen > Diagramm > XY > Punkte und Linien >
https://adetnhugmo.cloudimg.io/v7/www.mikrocontroller.net/attachment/38117/NTC.pdf?width=800
Spannungsteiler Ausgangsspannung
Rv = R1
Rntc = R2
| Vcc = | 5,0 |
| Rv = | 10000 |
| Rntc = | 10000 |
| Us = | 2,500 |
|
|
=B10/(B11+B12)*B12 |
| PIC1023 = | 512 |
|
|
=B13/(B10/1023) |
Vcc / 1023
********************************************************I*
29) Linearisierung von resistiven Sensoren
1.2 Dreipunkt-Methode zur Berechnung von Rq
Bei dieser Methode wird Rq so gewählt, damit drei Punkte des Verlaufs von UR(x) auf einer Geraden liegen.
Üblicher weise werden dies die Endwerte UR(x1) und UR(x3) des zu linearisierenden Bereiches sein und ein Wert UR(x2) in etwa der Mitte des Bereichs.
Dabei verschwindet der Linearitätsfehler im Messwerte x2 exakt.
Zur Dimensionierung werden nur die drei Widerstandswerte R(x) des Sensors bei den drei Messgrößenwerten benötigt (R(x1)=R1).
Eine vereinfachte Formel für Rq ergibt sich, wenn x2 genau in der Mitte zwischen x1 und x3 liegt.
z.B
R1 = 33890 Ohm (bei 0 °C)
R2 = 10000 Ohm (bei 25 °C)
R3 = 3564 Ohm (bei 50 °C)
x2 genau in der Bereichsmitte
https://www.mikrocontroller.net/topic/189467
https://adetnhugmo.cloudimg.io/v7/www.mikrocontroller.net/attachment/86418/vu_linearisierung_rsens.pdf?width=800
********************************************************I*
30) Sensordateien für einfache Sensoren
Erstellung von Dateien am Beispiel von NTC- und LDR-Sensoren
Von Burkhard Kainka
Programme wie ModulLAB, Prisma oder CompyctDefinition verwenden Sensordateien, um unterschiedliche Sensoren mit ihren korrekten Einheiten darzustellen.
Man kann sich leicht eigene Sensordateien herstellen, wenn sie eine lineare Übertragungskennlinie haben.
Beispiel:
Ein DC-Motor als Drehzahlsensor liefert eine Generatorspannung, die proportional zur Drehzahl ist.
Man braucht nur einen einzigen Messpunkt, um die Datei zu erstellen.
Dies erfolgt z.B.
Inzwischen gibt es eine Spezialversion dieses Programms für C-Control.
MesskalC, das Sensor-Kalibrierprogrammfür C-Control und ModulLAB (Messkalc.zip, 66 KB)
Mit etwas Aufwand geht es aber doch.
Oft läst sich dann ein preiswerter Sensor für einfache Messungen verwenden.
Ein NTC-Widertand wird in erster Näherung nur durch zwei Werte beschrieben:
Den Nennwiderstand R25 und den B-Wert.
Für den im SIOS- und CompuLAB-Experimentierset verwendeten Typ mit 4,7k oder 10k konnten aber die B-Werte erfragt werden.
Für den Standard-NTC-Widerstand von 10k wurde ein B-Wert von 4300 K angegeben, für den 4,7k NTC B=3950 K.
Beide Sensoren werden im Normalfall in einer Spannungsteilerschaltung eingesetzt,
Die Auswertung wird hier für Excel beschrieben. In der A-Spalte kann man sich einige Temperaturen eintragen.
Der Widerstand berechnet sich dann für den 10k NTC mit der folgenden Formel.
Rt = 10000 * EXP (4000 * (1/(273,15+0) - 1/(273,15+25)))
Rt = 10000 * EXP (4300 * (1/(273,15+A) - 1/298,15))
Man kann sich damit leicht den kompletten Widerstandsverlauf aufzeichnen lassen.
Für die Herstellung einer Sensortabelle ist die Aufgabe aber anders:
Der AD-Wandler liefert einen Wert zwischen 0 und 255 für den Bereich von 0 V bis zur Referensspannung von z.B. 5 V.
Aus diesem Ergebnis muss zunächst nach den Gesetzen der Reihenschaltung der Widerstand des Sensors bestimmt werden.
In Excel trägt man in der A-Spalte eine Zahlenfolge von0 bis 255 ein.
=(2550-10*A:A)/A:A
Aus diesem Widerstand kann nun in Spalte C die Temperatur berechnet werden:
=1/(LN(B:B/10)/4300+1/298)-273
Wenn man nun die wunderschönen Temperaturangaben sieht, könnte man fast dran glauben.
Allerdings muss man sich immer vor Augen halten, dass der Nennwidertsand mit einer Toleranz von +/-5% angegeben wird.
Das entspricht einer möglichen Abweichung von ca. +/-1 K bei 25 °C.
Um die gewonnene Temperaturtabelle in die Sensortabelle zu übertragen, verwendet man am besten ein Vorbild, das umgebaut wird.
Die DEF-Datei enthält neben der reinen Text-Tabelle noch eine zweite Tabelle, die die relative Plot-Position für jeden Messwert angibt.
=(C:C+20)/80
Da in Spalte C auch Werte unter -20 C und über +60 C auftreten, gibt es nun zunächst auch Plotpositionen unter Null und über Eins.
Zum Schluss muss noch des Dateikopf etwas angepasst weren.
Grad : T
Einheit: °C
Y-Achse: T/°C
Position X-Achse: 0.250
Position Beschriftung
0.000 -20
0.125 -10
0.250 0
0.375 10
0.500 20
0.625 30
0.750 40
0.875 50
1.000 60
Zuordnung 0...255
-60.0
-57.6
-49.9
-45.0
-41.4
Die fertige Datei wird unter dem Namen NTC10k.DEFgespeichert.
Das stimmt.
Aber wenn man mal einen andern Sensor hat oder ein ähnliches Problem lösen will, findet man hier die nötigen Arbeitsschritte.
http://www.elexs.de/modulbus/compas/compas27/ntc10k.def
Der LDR-Sensor
Jeder LDR-Sensor hat eine ganz bestimmte Kennlinie. In erster Näherung erhält man im doppelt-logarithmischen Maßstab eine Gerade, wenn der Widerstand gegen die Helligkeit aufgetragen wird.
Viele Anwender von ELEXS oder SIOS haben bereits einen ganz bestmmten LDR-Sensor mit der Typenbezeihnung A9060-14.
I R
1 lux ca. 1500 k
10 lux ca. 150 k
100 lux ca. 15 k
1000 lux ca. 2 k
10000 lux ca. 0,3 k
Mit Excel wurde versucht, eine möglichst gute Näherung zufinden.
Das Ergebnis ist folgende Gleichung:
R = 1350 / EXP [1,042 LN(I) - 0,015 (LN(I))²]
Mit etwas Mühe kann man diese Gleichung so umstellen, dass die Helligkeit I in Lux geliefert wird.Dann können ähnliche Methoden wie beim NTC-Sensor angewandt werden, um eine vorhandene Sensortabelle für den LDR umzurüsten.
Ausgangspunkt war hier die Datei Licht_E.DEF. Das fertige Ergebnis LDR1.DEF kann hier geladen werden.
Auch hier wieder gilt: Man sollte sich nicht durch die schönen Zahlen blenden lassen.
Größe: E
Einheit: lux
Y-Achse: E/lux
Position X-Achse: 0.165
Position Beschriftung
0.008 0.1
0.165 1
0.326 10
0.478 100
0.635 1000
0.792 10000
0.949 100000
Zuordnung 0...255
0
1
1
2
Quelle:
10000 Ohm
=$J$2*$J$1/(B16+$J$1) =1,24
=KÜRZEN(C16/$J$2*(2^$J$3);0) = 63
=1000*$J$2/($J$1+B16) = 0,38
=(A16-A15)/(D16-D15) = 0,50
NTC-Tabelle_1a.xls
Quelle:
10k NTC - Mikrocontroller.net
********************************************************I*
32) Steinhart-Hart-Gleichung ?????
NTC und Steinhart-Hart-Gleichung - Mikrocontroller.net
Ich beschäftige mich zur Zeit mit der Temperaturmessung mittels eines Heißleiters und AD-Umsetzers.wobei R0 der Nennwiderstand und T0 die Nenntemperatur ist, die bei meinembenutzen NTC jeweils 10k Ohm und 25 °C betragen.
Die Gleichung enthält noch ein quadratisches Glied, welcher aber öfters weggelassen wird, da der Wert vernachlässigbar klein ist.
T1=253,15 K - 273,15 = -20 °C
Die Berechnung der Koeffizienten erfolgten in dem selbst geschriebenen Programm, welches über den SerialPort den AD-Wert vom Mikrocontroller (Atmega8) holt und diesen anschließend berechnet und zwar einmal nach der allgemeinen, ungenauen, Berechnungsgleichung (Gleichung 1)
33) Steinhart-Hart NTC - Links
Steinhart-Hart Thermistor Calibration in Excelhttps://www.mathscinotes.com/2019/11/steinhart-hart-thermistor-calibration-in-excel-using-matrix-formulas/
Thermistor Calibration and the Steinhart-Hart Equation - Applikation
CYPRESS Applikations Note AN2017
PSoC® 1 Temperature Measurement With Thermistor
https://www.cypress.com/file/125811/download
Wie misst man die Temperatur mit einem NTC-Thermistor?
https://qastack.com.de/electronics/8754/how-to-measure-temperature-using-a-ntc-thermistor
Formeln in Excel einfrieren und Festwerte übertragen
https://www.computerwissen.de/software/office/excel/tabellen-excel/tabellen-formatieren-diese-moeglichkeiten-bietet-excel/nur-die-ergebnisse-von-formeln-als-festwerte-in-excel-anzeigen/
NTC und Steinhart-Hart-Gleichung
https://www.mikrocontroller.net/topic/210255
https://de.wikipedia.org/wiki/Steinhart-Hart-Gleichung
Temperaturmessung mit NTC Thermistoren
https://devxplained.eu/de/blog/temperaturmessung-mit-ntcs
Regression des Widerstands eines Thermistors
http://www.physik.li/publikationen/Thermistor.pdf
Einstellungen und Anwendungshinweise zur EL3204-0200
https://infosys.beckhoff.com/index.php?content=../content/1031/el32xx/1525745803.html&id=
NTC Thermistor Widerstandsrechner
https://ntcsensors.com/NTC_Thermistor_Widerstands_rechner/
NTC Thermistor mit ARDUINO UNO
https://robolabor.ee/homelab/de/examples/sensor/thermistor
Wie erhalte ich A-, B- und C-Werte für diesen Thermistor?
https://qastack.com.de/electronics/51865/how-to-get-a-b-and-c-values-for-this-thermistor
Wie man mit Thermistoren die Temperatur genau messen kann
https://www.digikey.at/de/articles/how-to-accurately-sense-temperature-using-thermistors
NTC-Thermistoren - Beta-Werte berechnen | Ametherm
https://ntcsensors.com/NTC_Thermistor_Preis/
https://ntcsensors.com/Thermistor_rechner_Datenblatt_PDF/
https://ntcsensors.com/Hersteller_von_NTC_10k_Ohm_Sensoren/
https://ntcsensors.com/Symbole_und_Formeln_von_NTC__und_PTC_Thermistoren/
https://ntcsensors.com/Thermistor_Einheit/
https://ntcsensors.com/NTC_Sensor_tabelle/
https://ntcsensors.com/10k_NTC_Thermistortabelle/
Bestimmung von Thermometerkennlinien
https://www.ptb.de/cms/fileadmin/internet/dienstleistungen/dkd/archiv/Publikationen/Richtlinien/DKD-R_5-6_2018-09_rev1.pdf
Bestimmung der Messunsicherheiten bei der Temperaturmessung mit Oberflächen-Tasttemperaturfühlern
https://www.db-thueringen.de/servlets/MCRFileNodeServlet/dbt_derivate_00025260/ilm1-2011200608.pdf
Temperaturen mittels Thermistor und seriellen Plotter der Arduino IDE als Graph darstellen
https://42project.net/temperaturen-mittels-thermistor-und-seriellen-plotter-der-arduino-ide-als-graph-darstellen/
App
Thermometer Calculator
https://play.google.com/store/apps/details?id=com.vernshome.thermocalc&hl=de_AT&gl=US
Heißleiter, NTC-Widerstand oder NTC-Thermistor
https://de.linkfang.org/wiki/Heißleiter
Software zur Thermistor Berechnung
http://thermistor.sourceforge.net/
Das Schema und Funktionsprinzip des Thermistors
https://female-page.ru/de/useful-purchase/scheme-and-operating-principle-of-the-thermistor-thermistors.html
Voltage Divider Circuit Calculator - For NTC Thermistor
https://www.petervis.com/electronics%20guides/calculators/thermistor/thermistor.html
Potential Divider with NTC Thermistor
https://www.petervis.com/GCSE_Design_and_Technology_Electronic_Products/Potential_Divider/Potential_Divider_with_Thermistor.html
NTC Thermistor Beta Calculator
https://www.ametherm.com/thermistor/ntc-thermistor-beta
Measuring the temperature with NTCs
https://www.giangrandi.org/electronics/ntc/ntc.shtml
Calculating Temperature from Resistance
https://www.northstarsensors.com/calculating-temperature-from-resistance
EPCOS Standardized R/T Characteristics
300_d_EPCOS-x_Standardized R-T Characteristics - Formeln Tabelle R-T und alpha %-K_1a.pdf
https://www.electrokit.com/uploads/productfile/41012/0900766b80731548.pdf
Algorithm Execution Time and Accuracy of NTC Thermistor-Based Temperature Measurements in Time-Critical Applications
300_d_MDPI-x_NTC Thermistor-Based Temperature Measurements in Time-Critical Applications (16 Seiten)_1a.pdf
https://www.mdpi.com/2227-7390/9/18/2266/htm
Thermistor R_T Calculators _ QTI Sensing Solutions
NTC Thermistor Widerstandsrechner V2.0 - Electro Tech Online
Thermistor-Rechner - Cypress Semiconductor
SRS-Thermistorrechner - Stanford Research Systems
300_d_RUB-x_Skriptum Temperaturmessverfahren (46 Seiten)_1a.pdf
Ich verwende zur Zeit am Arduino die Standard NTC-Formel
T=B*Tn / (B+log (Rt/Rn)*Tn)
Wenn du die Daten des NTC hast dann kannst du auch die Standardgleichung nehmen.
Steinhart/Hart macht vor allem Sinn, wenn du die Kennlinie des NTC erst selbst ermitteln mußt.
Ich würde es aber trotzdem anders lösen.
Der ARDUINO ADC hat 10-bit (1024) Auflösung.
/*************************************************************************************************** NTClesen by Gunther Breu 2013 ****************************************************************************************************** Funktionsbeschreibung **** Aus AD Wert wird mittels SensTab ein Temperaturwert interpoliert **** Aus diesem Wird ein gleitender Mittelwert (Wertigkeit Tempfilterfaktor) gebildet. **** ADFehler bei < ValidUG oder > ValidOG **** **** Input: Sensornummer **** Output: nix **** genutzte Globale Variablen: TempSensorfehler, TempWerte ****************************************************************************************************/void NTClesen(int _SensorNr) { static boolean init = true; const int Tempfilterfaktor = 50; const int ValidUG 8 // festlegen der unteren Grenze für gültige AD-Werte const int ValidOG 1020 // festlegen der oberen Grenze für gültige AD-Werte /* Wertetabelle Sensor Werte */ const int Sensorpunkte 25 const float SensTab[Sensorpunkte][2]={{1, 911.940}, // Sensortabelle Accurite GT {8, 468.799}, {16, 385.986}, {35, 311.374}, {60, 268.223}, {90, 238.958}, {130, 214.158}, {180, 193.142}, {250, 172.321}, {350, 150.673}, {450, 133.529}, {530, 121.375}, {600, 111.237}, {665, 101.865}, {730, 92.173}, {790, 82.533}, {845, 72.580}, {890, 63.0}, {925, 53.940}, {955, 44.97}, {976, 35.18}, {992, 25.644}, {1008, 11.104}, {1016, -2.58}, {1023, -35.470}}; int SensorAD = analogRead(_SensorNr); // Überprüfen des AD-Signales auf Gültigkeit if (SensorAD < ValidUG || SensorAD > ValidOG){ TempSensorfehler = true; TempWerte = -99; } else{ TempSensorfehler = false; } if (!TempSensorfehler){ // Suchen des passenden Wertepaares zum Messwert int i = 0; while (i < Sensorpunkte && SensorAD > SensTab[i][0]){i++;} double Temp = ( ((SensTab[i][1] - SensTab[i-1][1]) * ( SensorAD - SensTab[i-1][0] )) // interpolieren der Werte zwischen / (SensTab[i][0] - SensTab[i-1][0] )) // Stelle i und Stelle i+1 + SensTab[i-1][1]; if (init){ // beim ersten Mal den Speicher des gefilterten Wertes initialisieren. init =false; TempWerte = Temp; } // Filterung der Sensorwerte TempWerte = ((TempWerte * Tempfilterfaktor) + Temp) / (Tempfilterfaktor +1); } } // End of NTClesen35) NTC-Widerstände - Grundlagen (1A)
Heißleiter-Meßschaltung mit Pufferstufe
300_b_D-Sensors-x_Kennlinie NTC-10k Ohm Temperatur Sensoren B=3976K (0 °C = 32,651k)_1a .pdf
********************************************************I*
Linearisierung / Wertermittlung

|
Widerstand bei der Temperatur 
|

|
Nennwiderstand bei Nenntemperatur |

|
absolute Betriebstemperatur |

|
Nenntemperatur (meist 25 °C, das heißt 298,15 K) |

|
Aktivierungsenergie, einstellbar über die Bandlücke des Halbleitermaterials |

|
Boltzmannkonstante |

|
Eulersche Zahl |
TN = 25°C + 273,15K Tn = 298,15K (25 °C = Temperatur bei Nennwiderstand)
37) WeTec's Technikseite NTC & PTC
Heißleiter (NTC), Kaltleiter (PTC) - Rechner
Ein PTC-Widerstand vergrößert seinen Widerstand bei steigender Temperatur(PTC - engl. Positive Temperature Coefficient).
Electronic Developer Online calculator
Einige Werte für die Eingabemaske müssen aus dem Datenblatt des ausgewählten NTC-Widerstandes übernommen werden.
In diesem Beispiel liegt der NTC auf Massepotenzial, mit dem Vorteil, dass sich Störeinflüsse über das Sensorkabel leichter wegfiltern lassen.
Die Änderung der Größe der Ausgangsspannung Vm erfolgt in diesem Beispiel umgekehrt zur Änderung der Temperatur.
Die Spannung Vm muss hochohmig ausgekoppelt werden, damit niederohmige Nachfolgestufen keine Verfälschungen dieses Signals vornehmen.
Erzeugt den C Code zur Umrechnung von ADC Werte eines Spannungsteilers mit NTC in °C.
Anzahl der Stützpunkte:Einheit in °C:
ADC Auflösung:
NTC Beschaltung:
NTC mit PullDown Widerstand
NTC mit PullUp Widerstand
PullUp/Down-Widerstand in Ohm:
Widerstand NTCs bei 25°C:
BETA Wert des NTCs:
Test resistance:
NaN°
Messbereich:
Von °C bis °C
Der Fehler durch die Verwendung einer Tabelle beträgt:0.088°C.
/**
* Die NTC Tabelle, bestehend aus 33 Temperaturstützpunkten.
* Einheit:0.01 °C
*
*/
int NTC_table[33] = {
-4399, -3403, -2407, -1739, -1217, -778,
-392, -42, 283, 589, 881, 1164, 1441, 1714,
1986, 2259, 2535, 2816, 3106, 3406, 3720,
4052, 4407, 4792, 5215, 5688, 6231, 6874,
7669, 8719, 10281, 13317, 16353
};
/**
* \brief Konvertiert das ADC Ergebnis in einen Temperaturwert.
*
* Mit p1 und p2 wird der Stützpunkt direkt vor und nach dem
* ADC Wert ermittelt. Zwischen beiden Stützpunkten wird linear
* interpoliert. Der Code ist sehr klein und schnell.
* Es wird lediglich eine Ganzzahl-Multiplikation verwendet.
* Die Division kann vom Compiler durch eine Schiebeoperation.
* ersetzt werden.
*
* Im Temperaturbereich von -10°C bis 50°C beträgt der Fehler
* durch die Verwendung einer Tabelle 0.088°C
*
* \param adc_value Das gewandelte ADC Ergebnis
* \return Die Temperatur in 0.01 °C
*
*/
int NTC_ADC2Temperature(unsigned char adc_value){
int p1,p2;
/* Stützpunkt vor und nach dem ADC Wert ermitteln. */
p1 = NTC_table[ (adc_value >> 3) ];
p2 = NTC_table[ (adc_value >> 3)+1];
/* Zwischen beiden Punkten linear interpolieren. */
return p1 + ( (p2-p1) * (adc_value & 0x07) ) / 8;
};
https://www.sebulli.com/ntc/index.php?lang=de&points=32&unit=0.01&resolution=8+Bit&circuit=pulldown&resistor=10000&r25=10000&beta=3500&test_resistance=NaN&tmin=10&tmax=50
********************************************************I*
Wird ein Widerstand parallel zu einem linearem Potentiometer geschaltet (siehe unten),
15. Spannungen vergleichen - Anschluss von Sensoren
Wir werden einen NTC-Widerstand zur Auslösung eines Schaltereignisses verwenden.
In der vorliegenden Schaltung sind der Vorwiderstand Rv und der Sensor (NTC) in Reihe oder in Serie geschaltet.
Die Formel ist nicht ganz einfach programmtechnisch umzusetzen.
Die beiden Diagramme entstanden durch Modellierung des Sachverhalts in Excel.
RN – NTC-Widerstandswert bei Bezugstemperatur TN (meistens 25°C). z.B. Rn = 10k
RT - Widerstandswert bei Meß-Temperatur T z.B. 50 °C
B – Thermistorkonstante laut Datenblatt z.B. B = 2000K
R2 bei 25 °C Nenntemperatur
R3 bei 45 °C
Um beste Ergebnisse zu erzielen, wählen Sie Punkte so aus, dass zwei nahe an den Extremen des Betriebsbereichs liegen und ein dritter nahe der Mitte.
Wenn eine Zahl eingegeben wird, klicken Sie außerhalb, um die Berechnung zu starten.
Verwenden Sie niemals die Eingabetaste.
44b) NTC Thermistors Steinhart and Hart Equation
NTC-Thermistoren sind nichtlineare Widerstände, die ihre Widerstandseigenschaften mit der Temperatur ändern. Einfach ausgedrückt, nimmt der Widerstand des Thermistors mit steigender Temperatur ab.
Beta wird in Grad Kelvin (K) gemessen und basierend auf der unten angegebenen Formulierung berechnet.
R t1 = Widerstand bei Temperatur 1
R t2 = Widerstand bei Temperatur 2
T1 = Temperatur 1 in (°K)
T2 = Temperatur 2 in (°K)
Der Beta-Wert eines NTC-Thermistors wird mit nur 2 Temperaturen über einen bestimmten Bereich berechnet
Eine genauere Methode ist die Verwendung der Steinhart- und Hart- Methode, die drei Temperaturen über einen bestimmten Bereich verwendet.
Weitere Informationen finden Sie in unserem Blogbeitrag über das Geheimnis erfolgreicher Thermistor-Beta-Berechnungen .
Wie berechnet man Beta?
Thermistor Beta Berechnungen verwenden , um eine Zwei-Punkt - Kalibrierung zur Berechnung des Widerstands gegen die Temperaturkurve und berücksichtigen den erforderlichen Widerstand bei beiden Temperaturpunkten.
Der Beta-Wert wird in Grad Kelvin und nicht in Fahrenheit oder Celsius gemessen und anhand der vier unten aufgeführten Komponenten berechnet.
4 Schlüsselkomponenten der Thermistor-Beta- Kalkulationen
R T1 = Widerstand bei Temperatur 1
R T2 = Widerstand bei Temperatur 2
T 1 = Temperatur 1 (K)
T 2 = Temperatur 2 (K)
Anwenden von Thermistor-Beta-Berechnungen
In der folgenden Beispielrechnung ging es darum, im Rahmen eines Projekts zur Restaurierung eines antiken Röhrenradios einen Thermistor mit dem angegebenen Widerstand zu finden.
NTC - Thermistor Beta Berechnungen verwenden , um eine Zwei-Punkt - Kalibrierung zur Berechnung des Widerstands gegen die Temperaturkurve und berücksichtigen den erforderlichen Widerstand bei beiden Temperaturpunkten.
Der Beta-Wert wird in Grad Kelvin und nicht in Fahrenheit oder Celsius gemessen und anhand der vier unten aufgeführten Komponenten berechnet.
4 Schlüsselkomponenten der NTC- Thermistor- Beta- Kalkulationen
R T1 = Widerstand bei Temperatur 1
R T2 = Widerstand bei Temperatur 2
T 1 = Temperatur 1 (K)
T 2 = Temperatur 2 (K)
Der größte Teil des AMWEI NTC- Thermistor- Beta-B-Werts wird aus Messungen bei 25 °C und 50 °C oder 25 °C und 85 °C berechnet,
die in B(25/50) oder B(25/85) oder dem anderen Temperaturpunkt, den der Benutzer am meisten interessiert, ausgedrückt werden .
Formel zur Berechnung des Beta-Werts
Temperatur oder Widerstand mit den B-Wert eines NTC berechnen
Beginnen wir mit der Formel von Wikipedia:

wir subtrahieren 1/T_N von beiden Seiten:
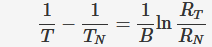
und multiplizieren beide Seiten mit B:

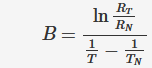
Jetzt brauchen wir noch zwei Datenpunkte.
Temperaturkoeffizient bezieht sich auf den Temperaturanstieg von 1 Grad, Widerstandsänderungsrate.
Thermistortemperaturkoeffizient = B-Wert / T ^ 2 (T ist die absolute Temperatur des zu konvertierenden Punktes)
B-Wert Berechnungsformel:
T1 / T2 ist in der Regel 25/85 oder 25/50 oder 25/100, abhängig von der Definition der verschiedenen Hersteller
R1 = der Widerstandswert bei der Temperatur T1
R2 = Widerstand bei Temperatur T2
T1 = 298,15 K (273,15 + 25 ° C) ist als Kay-Temperatur definiert
T2 = 358,15 K (273,15 + 85 ° C) ist als Kay-Temperatur definiert
Dieser Parameter ähnelt der Steigung der RT-Kurve des NTC-Produkts.
44d) NTC Thermistor Beta Value Calculator b-Wert Beta-Wert B25/50
Nicht sicher?
Klicken Sie hier, um ein Video zur NTC-Berechnung anzusehen.
- A, B, C are calibration parameters.
- R is the thermistor resistance (Ω).
- T is the thermistor temperature (K).
About this calculator
This calculator computes the resistance R1R_1R1 of an NTC thermistor at a target temperature T1T_1T1 based on the formula
where R0R_0R0 is the reference resistance at the reference temperature T0T_0T0 and the β\betaβ parameter defines the thermistor's temperature dependence.
Eine Linearisierung über Tabelle ist mit einem µCdie einfachste Lösung.
48a) Arduino Tutorial: Der Temperatursensor mit NTC
Rt = Gleich der ermittelte Widerstand abhängig von der Temperatur
Rn = Der Widerstand bei Nenntemperatur (hier 100k Ohm)
B = der angegebene B-Wert vom Hersteller (hier 3950K Kelvin)
Tn = Die Nenntemperatur in Kelvin ( = 273,15K Kelvin + 25°C = 298,15K Kelvin)
T = Die gemessene Temperatur ( den Wert wollen wir haben)
Wir kennen jeden Wert außer Rt. Der ist von der Temperatur abhängig und den müssen wir mit unserem Arduino messen. Aber wie kriegt man das hin?
Nun haben wir alles um die Temperatur zu berechnen.
Weiter unten findest du eine Schaltung und einen Beispielsketch mit den man alle wichtigen Werte für den NTC auf den seriellen Monitor darstellen kann.
Was benötigst du?
1x Arduino
1x Steckbrett
1x Widerstand (100kOhm)
1x NTC(Nennwiderstand100kOhm und B-Wert 3950Kelvin)
Jumperkabel (männlich)
int sensorPin = A0;
int bitwertNTC = 0;
long widerstand1=100000; //Ohm
int bWert =3950; // B- Wert vom NTC
double widerstandNTC =0;
double kelvintemp = 273.15; // 0°Celsius in Kelvin
double Tn=kelvintemp + 25; //Nenntemperatur in Kelvin
double TKelvin = 0; //Die errechnete Isttemperatur
double T = 0; //Die errechnete Isttemperatur
void setup() {
Serial.begin(9600);
}
void loop() {
if (Serial.available()>0) // Wenn serielle Kommunikation vorhanden
{
Serial.println("Sensormessung: ");
bitwertNTC = analogRead(sensorPin); // lese Analogwert an A0 aus
widerstandNTC = widerstand1*(((double)bitwertNTC/1024)/(1-((double)bitwertNTC/1024)));
// berechne den Widerstandswert vom NTC
TKelvin = 1/((1/Tn)+((double)1/bWert)*log((double)widerstandNTC/widerstand1));
// ermittle die Temperatur in Kelvin
T=TKelvin-kelvintemp; // ermittle die Temperatur in °C
Serial.println("Analog: "); //
Serial.println(bitwertNTC); //
Serial.println("NTC- Widerstand: "); //Gebe die ermittelten Werte aus
Serial.println(widerstandNTC); //
Serial.println("Temperatur: "); //Gebe die ermittelten Werte aus
Serial.println(T); //
delay(1000); // Warte eine Sekunde und mache alles nochmal
}
}
> if (Serial.available()>0) // Wenn serielle Kommunikation vorhanden
Das prüft nicht, ob eine serielle Schnittstelle vorhanden ist, sondern ob bytes im Ausgangspuffer liegen.
Korrekt wäre:
> if (Serial.available()==0) // Wenn gerade nicht gesendet wird
oder man lässt das if einfach weg.
Nr.10 Temperatur messen
int TMP36 = A0; //Der Sensor soll am analogen Pin A0 angeschlossen werden. Wir nennen den Pin ab jetzt "TMP36"int sensorwert;int temperatur = 0; //Unter der Variablen "temperatur" wird später der Temperaturwert abgespeichert.int t=500; //Der Wert für „t“ gibt im Code die zeitlichen Abstände zwischen den einzelnen Messungen vor.void setup() {Serial.begin(9600); //Im Setup beginnt die serielle Kommunikation, damit die Temperatur an den serial monitor übertragen wird. Über die serielle Kommunikation sendet das Board die Messwerte an den Computer. In der Arduino-Software kann man unter „Werkzeuge“ den „Seriellen Monitor“ starten um die Messwerte zu sehen.}void loop() {sensorwert=analogRead(TMP36); //Auslesen des Sensorwertes.temperatur= map(sensorwert, 0, 410, -50, 150); //Umwandeln des Sensorwertes mit Hilfe des "map" Befehls.delay(t); // Nach jeder Messung ist je eine kleine Pause mit der Dauer „t“ in Millisekunden.Serial.print(temperatur); //Nun wird der Wert „temperatur“ über die serielle Kommunikation an den PC gesendet. Durch öffnen des seriellen Monitors in der Arduino-Software kann die Temperatur abgelesen werden.Serial.println(" Grad Celsius"); // Im seriellen Monitor wird hinter der Temperatur die Einheit eingeblendet.}
VISHAY 2381 640 3/4/64103 10000 Ohm B25/85= 3977K
| 0,0033540160000 | 0,0002569850000 | 0,0000026201300 | 0,0000000638309 | 10000 | 10000 | R |
| A1 | B1 | C1 | D1 | Rref | R |
|
|
|
|
|
|
298,15 | 25,0 | °C |
| =1/( A1 + (B1*log(F1/E1)) + (C1*(log(F1/E1)^2)) + (D1*(log(F1/E1)^3)) ) |
|
|
|
|
=E3-273,15 |
|
Konstanten für die Berechnung der Temperatur aus NTC-Widerstand
B25 = 3977K
Rref = 2200 Ohm
A1=3.354016E-03 0.003354016
B1=3.2569850E-04 0.0002569850
C1=2.61013E-06 0.00000262013
D1=6.38309e-08 0.0000000638309
R = Widerstand des NTC bei Meßtemperatur
https://blog.fh-kaernten.at/ingmarsretro/tag/temperaturmessung-mit-arduino/
Standardized R/T characteristics
int aValue = analogRead(ANALOGPIN); // Temperatur einlesen (NTC 10k bei 25°C, Materialkonstante 3950, Vorwiderstand 47,3 k) Temp_NTC = (ABSZERO + 25) * 3950 / (3950 + (ABSZERO + 25) * log((47300 * ((aValue / MAXANALOGREAD))) / (1 - (aValue / MAXANALOGREAD)) / 10000)) - ABSZERO; Serial.print("NTCB: ");
Serial.print(Temp_NTC);
Serial.println(" C"); delay(1000); Temperatur();
273,15 -30 °C = 243,15
273,15 = 0,00 °C
298,15 K − 273,15 = 25,00 °C
Sensorkennlinien
B-Werte bei B(25/50) =3950K (mittlere Wert zwischen 25 und 50°C)
B-Werte bei B(25/100)=3996K (mittlere Wert zwischen 25 und 100°C)
Temperatur immer in Kelvin (es gibt keine minus Grade)
Rt=A*e^(B/T)
Rt = R25 * e ^ (B * (1/T - 1/T25))
Rt = R25 * e ^ (B * (1/T - 1/T25)) kann in
Rt=R25*e^(B/T) umgeformt werden, wobei gilt: A = R25 * e ^ (-B/T25) ????
R25= 15k 0hm bei 25 °C
B = ln(R/R25)/(1/T-1/T25)
300_fritz-x_NTC Widerstands- und Temperaturwerte bei 15k (Diagramm)_1c.xls
Für dieses Projekt gibt es auch ein Video auf Youtube: Arduino Temperatur analog messen mit einem NTC Widerstand über Spannungsteiler
Ein NTC ist ein temperaturabhängiger Widerstand, der sehr einfach mit einem Mikrocontroller ausgelesen werden kann.
NTC vs PTC
Der NTC (Negative Temperature Coefficient) wird auch als Heißleiter bezeichnet.
Der PTC (Positive Temperature Coefficient) wird auch als Kaltleiter bezeichnet und funktioniert umgekehrt wie der NTC.
Der NTC am Arduino
Der NTC kann mit allen Mikrocontroller verwendet werden, da es sich hier lediglich um einen analogen Spannungswert handelt.
Fazit - NTC Temperatur Widerstand
Ein großer Vorteil von temperaturabhängigen Widerständen ist, dass für die Mikrocontroller keine Library oder komplizierte Software benötigt wird.
Das spart Speicher und ist vor allem auch für Anfänger ein guter Einstieg in die Sensorik.
Der Sensor selbst reagiert sehr schnell auf Veränderungen von Temperatur.
Der NTC hat aber auch einige kleine Nachteile:
Da der Sensor analog ist, sollte er immer mit einem anderen genauen Temperatursensor abgeglichen werden.
Bei unseren Tests stellten wir fest, dass die Genauigkeit bei +/- 1,6 Grad liegt.
Für exakte Messungen, wie es zum Beispiel bei einer Wetterstation erwünscht ist, sollte auf diese Art von Sensoren verzichtet werden
und ein digitaler Sensor verwendet werden.
Wer nur annähernd einen Temperaturwert ermitteln will, wird mit dieser Lösung sehr zufrieden sein.
Außerdem ist das die wirklich einfachste und günstigste Lösung für eine Temperaturmessung.
Temperaturmessung mit NTC (Spannungsteiler, Arduino)
In dem Experiment messen wir Temperatur mithilfe eines Heißleiters.
Im nächsten Schritt müssen wir die B-Konstante ermitteln. Sie wird benötigt, um spätere Spannungswerte in Temperatur umzurechnen.
Berechnung der B-Konstante
Berechnung der NTC-Widerstände
https://www.meine-schaltung.de/rechner/temperatur/ntc/
Den Widerstandswert von ca. 10 kOhm (10,11 k) erreicht der Fühler bei ca. 23 °C.
Weitere Berechnungen anhand des Diagramms ergaben, dass wir mit dem so ermittelten Wert der Thermistorkonstante B theoretisch eine Messgenauigkeit von +/- 0,5 °C erreichen könnten.
Bei dem praktischen Test stellte sich heraus, dass die Abweichungen höher liegen und Werte von über 1°C erreichten.
Die Unterschiede sind hier auf die einfachen und ungenauen Messmethoden zurückzuführen.
Für ein einfaches Thermometer sind die Ergebnisse jedoch durchaus zufriedenstellend.
Schaltplan
Der Sketch
Die aktuelle Temperatur wird im Programm in drei Schritten ermittelt:
1. Berechnung der Spannung am analogen Eingang
2. Berechnung des Widerstandswertes des NTC-Widerstandes
3. Berechnung der aktuellen Temperatur
// Temperatur-Messung mit NTC
// Spannungsteiler
// Arduino Nano, IDE 1.8.13
#include <TM1637Display.h> // Anzeige Bibliothek#define CLK 6#define DIO 7TM1637Display display(CLK, DIO);int R = 9910; // Spannungsteiler, fester Widerstandfloat Rn = 10110; // gemessen (Ohm)float Tn = 23; // gemessen (°C)float B = 3398; // Thermistorkonstante B (errechnet)void setup() { display.setBrightness(10); display.clear();}void loop() { float Analog_Wert = (float)analogRead (A0); // analogen Wert A0 auslesen float U_ntc = (5.2 * Analog_Wert) / 1023; // Spannung float R_ntc = (U_ntc * Rn) / (5.2 - U_ntc); // Widerstand // Temperatur-Berechnung // Rt = Rn * e hoch B*(1/T - 1/Tn) // Ausgangsformel // T = 1 / [(log(Rt/Rn)/B + 1/Tn] - 273,15 // umgestellt in °K // Tnk = 26,2 + 273,15 // °K float A1 = log(R_ntc / Rn) / B; float A2 = A1 + 1 / (Tn + 273.15); float T = (1 / A2) - 273.15; display.showNumberDecEx(T, 0b00000000, false, 4, 4); // Anzeige delay(1000); // Wartezeit}
SketchArduino_NTC_Resistor.ino
Quelle:
https://www.meine-schaltung.de/schaltung/arduino/sensoren/temperaturmessung_ntc/
https://www.youtube.com/watch?v=s2hD4xNNRWM
https://www.meine-schaltung.de/notizbuch/arduino/
https://www.meine-schaltung.de/notizbuch/anzeige/TM1637/#Schaltungen_mit_TM1637
********************************************************I*
55) ARDUINO Temperaturmessung mit einem 10k NTC Widerstand
Teileliste
Arduino IDE (Tutorial wurde mit 1.6 erstellt)
Arduino Uno (oder ein anderes Modell)
Breadboard
Steckbrücken oder Kabel
10kΩ Widerstand
10kΩ NTC Widerstand
Die Wiederstandsänderung des Thermistors, sieht je nach Typ in etwa so aus.
Da sich der NTC Widerstand nicht linear verhält, müssen wir zur Temperaturberechnung die Steinhart-Hart-Gleichung verwenden.
// Konstanten
const long interval = 1000; // Interval wie oft die Temperatur abgefragt wird (milliseunden)
const int abfrageZahl = 5; // Je mehr abfragen, desto stabiler isr das Ergebnis, dauert aber länger
const int ntc = A0; // Pin für den 10kO NTC Wiederstand
const int ntcNominal = 10000; // Wiederstand des NTC bei Nominaltemperatur
const int tempNominal = 25; // Temperatur bei der der NTC den angegebenen Wiederstand hat
const int bCoefficient = 3977; // Beta Coefficient(B25 aus Datenblatt des NTC)
const int serienWiederstand = 10000; // Wert des Wiederstands der mit dem NTC in Serie geschalten ist
// Variablen
int abfrage[abfrageZahl]; // Array Variable für das Mitteln der Temperatur
float durchschnitt = 0; // Variable für das Mitteln der Temperatur
float temp; // Variable für die Berechnung der temperatur nach Steinhart
unsigned long letzteMillis = 0; // Speichert die letzte Zeit (millis) der Temperaturabfrage
void setup()
{
Serial.begin(9600); // Setzt die Baudrate für die Ausgabe am Serial Monitor auf 9600
pinMode(ntc, INPUT); // Setzt den Pin des NTC Wiederstands als Eingang
}
void loop()
{
// Erfasst die aktuelle Zeit für den Abfrageinterval
unsigned long aktuelleMillis = millis();
// Löst bei erreichen der Intervalzeit die Temperaturberechnung aus
if(aktuelleMillis - letzteMillis >= interval)
{
// speichert die Zeit der letzten Abfrage
letzteMillis = aktuelleMillis;
// Startet die Temperaturerfassungsroutine
temperaturberechnung();
}
// Ausgabe an den Seriellen Monitor
Serial.print("Temperatur ");
Serial.print(temp);
Serial.println(" *C");
}
void temperaturberechnung()
{
// Nimmt N Abfragen in einer Reihe, mit einem kurzen delay
for (int i=0; i < abfrageZahl; i++)
{
abfrage[i] = analogRead(ntc);
delay(10);
}
// Mittelt alle Abfragen
durchschnitt = 0;
for (int i=0; i < abfrageZahl; i++)
{
durchschnitt += abfrage[i];
}
durchschnitt /= abfrageZahl;
// Umwandlung des Wertes in Wiederstand
durchschnitt = 1023 / durchschnitt - 1;
durchschnitt = serienWiederstand / durchschnitt;
// Umrechnung aller Ergebnisse in die Temperatur mittels einer Steinhard Berechnung
temp = durchschnitt / ntcNominal; // (R/Ro)
temp = log(temp); // ln(R/Ro)
temp /= bCoefficient; // 1/B * ln(R/Ro)
temp += 1.0 / (tempNominal + 273.15); // + (1/To)
temp = 1.0 / temp; // Invertieren
temp -= 273.15; // Umwandeln in °C
}
-
ntcNominal = 10000 - Damit ist der Widerstand des NTC bei Nominaltemperatur gemeint.
-
Dieser Wert wird immer im Namen schon angegeben.
- Ein 10k Ohm NTC hat einen Widerstand von 10000Ω.
- tempNominal = 25 - Das ist die Nominaltemperatur. Diese ist im Normalfall 25°.
- bCoefficient = 3977 - Der Beta Coefficient ist eine Materialkonstante und ist im Datenblatt des NTC zu finden und wird mit B25 bezeichnet.
- serienWiederstand = 10000 - Das ist der Wert in Ohm, des Widerstand, der zusammen mit dem NTC Widerstand verbaut wird. In unserem Fall auch ein 10kΩ Widerstand.
- abfrageZahl = 5
- abfrage[abfrageZahl]
Der Code startet mit der Abfrage ob die im interval festgelegte Zeit (im Beispiel 1000 Millisekunden) erreicht ist.
Hier wird als erstes der NTC so oft ausgelesen und dessen Werte gespeichert wie mit abfrageZahl festelegt ist.
Als nächstes werden die Werte zusammengezählt und durch abfrageZahl geteilt um den durchschnitt zu bilden.
Jetzt wird der durchschnitt in einen Widerstandswert umgerechnet. Ist das erledigt, wird die Temperatur mittels der Steinhart Formel berechnet.
Zurück im loop wird die Berechnete Temperatur in °C im Seriellen Monitor ausgegeben.
Dazu schauen wir uns den sogenannten Thermistor an.
Thermistoren sind Halbleiter- Widerstände. Ihr Widerstand hängt von der Umgebungstemperatur ab.
Der NTC
Wie gesagt ist der NTC ein Heißleiter und sein Widerstand sinkt, je höher die Umgebungstemperatur ist.
Viele Hersteller bieten einen Datenblatt an, wo man im bestimmten Abständen den Widerstand einer bestimmten Temperatur zuordnen kann.
RT = Gleich der ermittelte Widerstand abhängig von der Temperatur
RN = Der Widerstand bei Nenntemperatur (hier 100kOhm)
B = der angegebene B-Wert vom Hersteller (hier 3950Kelvin)
TN = Die Nenntemperatur in Kelvin ( = 273,15 Kelvin + 25°C = 298,15Kelvin)
T = Die gemessene Temperatur ( den Wert wollen wir haben)
Um nun den NTC Widerstand ermitteln zu können müssen wir deswegen den Nennwiderstand RN,
also einen 100 Kiloohm Widerstand, in Reihe zu dem NTC zuschalten um einen Spannungsteiler zu erzeugen.
Die gesamte Spannung Uges teilt sich nun auf den NTC und den 100 Kiloohm- Widerstand auf.
Mit der Spannungsteilerregel können wir anschließend RT berechnen.
Die Spannungsteilerregel sagt, dass in einer Reihenschaltung das Verhältnis zwischen Gesamtspannung Uges
und Gesamtwiderstand Rges genauso groß ist, wie das Verhältnis zwischen der Spannung UNTC, der an einem Widerstand (hier der NTC) abfällt und sein Widerstandswert RT.
Der Gesamtwiderstand Rges ergibt sich aus den 100 Kiloohm- Widerstand, addiert mit dem Widerstandswert vom NTC- Widerstand RT.
Die Spannung UNTC, die über dem NTC abfällt, kann man mit dem A0- Pin am Arduino messen.
Nun haben wir alles um die Temperatur zu berechnen.
Weiter unten findest du eine Schaltung und einen Beispielsketch mit den man alle wichtigen Werte für den NTC auf den seriellen Monitor darstellen kann.
Was benötigt man?
1x Arduino UNO R3
1x Steckbrett
1x Widerstand (100kOhm)
1x NTC(Nennwiderstand100kOhm und B-Wert 3950Kelvin)
Jumperkabel (männlich)
int sensorPin = A0;
int bitwertNTC = 0;
long widerstand1=100000; //Ohm
int bWert =3950; // B- Wert vom NTC
double widerstandNTC =0;
double kelvintemp = 273.15; // 0°Celsius in Kelvin
double Tn=kelvintemp + 25; //Nenntemperatur in Kelvin
double TKelvin = 0; //Die errechnete Isttemperatur
double T = 0; //Die errechnete Isttemperatur
void setup() {
Serial.begin(9600);
}
void loop() {
if (Serial.available()>0) // Wenn serielle Kommunikation vorhanden
{
Serial.println("Sensormessung: ");
bitwertNTC = analogRead(sensorPin); // lese Analogwert an A0 aus
widerstandNTC = widerstand1*(((double)bitwertNTC/1024)/(1-((double)bitwertNTC/1024)));
// berechne den Widerstandswert vom NTC
TKelvin = 1/((1/Tn)+((double)1/bWert)*log((double)widerstandNTC/widerstand1));
// ermittle die Temperatur in Kelvin
T=TKelvin-kelvintemp; // ermittle die Temperatur in °C
Serial.println("Analog: "); //
Serial.println(bitwertNTC); //
Serial.println("NTC- Widerstand: "); //Gebe die ermittelten Werte aus
Serial.println(widerstandNTC); //
Serial.println("Temperatur: "); //Gebe die ermittelten Werte aus
Serial.println(T); //
delay(1000); // Warte eine Sekunde und mache alles nochmal
}
}
Danke für das Tutorial. Da ist aber noch ein Bock drin:
> if (Serial.available()>0) // Wenn serielle Kommunikation vorhanden
Das prüft nicht, ob eine serielle Schnittstelle vorhanden ist, sondern ob bytes im Ausgangspuffer liegen.
Korrekt wäre:
> if (Serial.available()==0) // Wenn gerade nicht gesendet wird
oder man lässt das if einfach weg. So ein Konstrukt wird hier nicht gebraucht.
ich habe definiert:
long widerstand1 = 4700; //vorgeschaltener Widerstand, Ohm
long widerstandR25 = 100000; //R25 Wert des NTC, Ohm
und in loop() folgende Formel angepasst:
TKelvin = 1 / ((1 / Tn) + ((double)1 / bWert) * log((double)widerstandNTC / widerstandR25)); // ermittle die Temperatur in Kelvin
In diesem Beispiel wird nur ein NTC gemessen und somit ist die zu messende Analogspannung (fast) immer gleich der Spannung der vorgehenden Messung.
Zum ausprobieren: A1 an Masse schalten und danach an +5V.
bitwertNTC = analogRead(sensorPin);
das einfügen:
int test = analogRead(A1);
Abhilfe:
* Spannungsteiler mit geringeren Widerstandswert benutzen (zB eine 4,7k Ohm NTC und entsprechenden 4,7k Ohm Festwiderstand)
* oder einen 0,1µF Kondensator von A0 anschluß auf Masse schalten (paralell zum NTC).
Code- Review
widerstandNTC = widerstand1*(((double)bitwertNTC/1023)/(1-((double)bitwertNTC/1023)));
Hier wird der NTC- Widerstandswert ermittelt.
TKelvin = 1/((1/Tn)+((double)1/bWert)*log((double)widerstandNTC/widerstand1));
Hier wird die Temperatur in Kelvin berechnet. Diese Zeile entspricht dieser Formel:
5.1 Der Thermistor als Temperatursensor
Thermistoren sind temperaturabhängige Widerstände.
PTC-Thermistoren werden häufig als rücksetzbare Sicherungen verwendet, da ein durch Temperaturanstieg erhöhter Widerstand den Stromfluss reduzieren kann.
Thermistoren haben einige Vorteile gegenüber Temperatursensoren auf Halbleiterbasis, denn sie können praktisch mit jeder Spannung arbeiten und sind leicht an einen Mikrocontroller anpassbar.
Kenngröße Wert (Beispiel)
Widerstand 25 °C 10k Ohm +/- 1%
Thermische Zeitkonstante 15 s
Messbereich -55 bis 125 °C
Tabelle 5.1 Kenngrößen von Thermistoren
Die Kennlinie für einen NTC-Thermistor zeigt Abbildung 5.1.
---- = A + B ln(R) + C(ln(R))3
Zur Berechnung der Temperatur sind in die Formel der Wert für To (25 °C = 298,15K), der Koeffizient B (hier 3950K), der Widerstandswert für Ro (der Widerstand des NTC bei Raumtemperatur, in diesem Fall 10k Ohm) und der gemessene Widerstandswert R einzutragen.
Zur Messung mit dem Arduino wird aus dem Thermistor und einem wertmäßig gleich großen Festwiderstand ein Spannungsteiler gebildet, dessen Spannung vom AD-Umsetzer des Arduino erfasst wird. Abbildung 5.2 zeigt das einfache Schaltbild.
steinhart = average / THERMISTORNOMINAL; // (R/Ro)
steinhart = log(steinhart); // ln(R/Ro)
steinhart /= BCOEFFICIENT; // 1/B * ln(R/Ro)
steinhart = 1.0 / steinhart; // Invert
steinhart -= 273.15; //1 convert to C
Ein NTC-Widerstand (Negative Temperature Thermistor) ist ein temperaturabhängiger Widerstand.
Ein NTC-Widerstand hat einen negativen Temperaturkoeffizienten,
Inhaltsverzeichnis [Ausblenden]
Bezug
Den mir vorliegenden NTC-Widerstand habe ich über eBay.de für 3,45 € inkl. Versandkosten erstanden.
Technische Daten eines NTC-Widerstand
Die technischen Daten eines NTC-Widerstandes sind sehr übersichtlich, denn dieses Bauelement ist im übertragenen Sinn „nur“ ein Widerstand welcher bei einer Temperaturänderung seinen Widerstandswert ändert. Der Nennwiderstand von 10k Ohm wird hier immer bei einer Temperatur von 25 °C angegeben.
Schaltung
Für die nachfolgende Schaltung verwende ich einen 10k Ohm NTC-Widerstand und einen 10k Ohm Kohleschichtwiderstand.Wenn du einen 100 Ohm NTC-Widerstand verwendest, so musst du auch einen 100 Ohm Widerstand verwenden usw.
Wie bereits erwähnt ist die Schaltung eine Spannungsteilerschaltung wo man an 2 Punkten die Spannung misst und dann vergleicht.
Aufbau der Schaltung
Für den Aufbau der Schaltung benötigst du:1x Arduino UNO,
1x Breadboard mit 170 Pins, besser noch 400 Pins,
1x Kohleschicht / Metallschicht Widerstand mit 10k Ohm,
1x NTC-Widerstand mit 10k Ohm,
ARDUINO Sketch
Ermitteln des Widerstandswertes am analogen Ausgang
Zunächst einmal müssen wir den Wert des NTC-Widerstandes ermitteln.Das Arduino Board hat kein Widerstandsmessgerät verbaut, sondern eher ein Spannungsmesser.
Wir können an den analogen Pin Spannungen von max. 5V anlegen und dieses wird uns dann in Werten von 0 bis 1023 wiedergegeben.
Somit ergibt sich erstmal folgender einfacher Sketch zum Ermitteln des Widerstandswertes:
Umrechnen des Widerstandwertes in ein Temperaturwert
Im ersten Schritt haben wir den Widerstandswert des NTC-Widerstandes ermittelt, nun wollen wir diesen Wert in einen Temperaturwert umwandeln.In dem Buch „Sensoren im Einsatz mit Arduino“ ist eine relativ einfache Formel abgebildet (leider ohne Erläuterung) in dem Tutorial von Adafruit ist ein Beispiel wie dieses mit der Steinhart-Hart Formel berechnet wird.
Ich persönlich finde die Lösung vom Buch deutlich schlanker und lesbarer.
Quellen
Für dieses Tutorial habe ich folgenden Artikel aus Wikipedia verwendet.
Seite „Heißleiter“. In: Wikipedia, Die freie Enzyklopädie.
Des Weiteren habe ich das Tutorial zum Heißleiter von Adafruit verwendet, dort werden die Formeln für das Umrechnen eines Widerstandswertes in einen Temperaturwert gezeigt.
Hier nun der Wikipedia Artikel zur Steinhart-Hart Formel:
Seite „Steinhart-Hart-Gleichung“. In: Wikipedia, Die freie Enzyklopädie.
(LM35/TMP36 (https://adafru.it/aK2) ) or digital temperature sensor chips (DS18B20) or
thermocouples (https://adafru.it/cl0).
// https://learn.adafruit.com/thermistor/using-a-thermistor by Limor Fried, Adafruit Industries
// MIT License - please keep attribution and consider buying parts from Adafruit
// the value of the 'other' resistor
// What pin to connect the sensor to
#define THERMISTORPIN A0
void setup(void) {
Serial.begin(9600);
}
float reading;
reading = analogRead(THERMISTORPIN);
Serial.print("Analog reading ");
Serial.println(reading);
// convert the value to resistance
reading = (1023 / reading) - 1; // (1023/ADC - 1)
reading = SERIESRESISTOR / reading; // 10K / (1023/ADC - 1)
Serial.print("Thermistor resistance ");
Serial.println(reading);
delay(1000);
}
// https://learn.adafruit.com/thermistor/using-a-thermistor by Limor Fried, Adafruit Industries
// MIT License - please keep attribution and please consider buying parts from Adafruit
// which analog pin to connect
// how many samples to take and average, more takes longer
// but is more 'smooth'
#define NUMSAMPLES 5
// the value of the 'other' resistor
Serial.begin(9600);
// connect AREF to 3.3V and use that as VCC, less noisy!
analogReference(EXTERNAL);
}
uint8_t i;
float average;
for (i=0; i< NUMSAMPLES; i++) {
samples[i] = analogRead(THERMISTORPIN);
delay(10);
}
average = 0;
for (i=0; i< NUMSAMPLES; i++) {
average += samples[i];
}
average /= NUMSAMPLES;
Serial.println(average);
// convert the value to resistance
average = 1023 / average - 1;
average = SERIESRESISTOR / average;
Serial.println(average);
}
// https://learn.adafruit.com/thermistor/overview by Limor Fried, Adafruit Industries
// MIT License - please keep attribution and consider buying parts from Adafruit
// which analog pin to connect
#define THERMISTORPIN A0
// resistance at 25 degrees C
#define THERMISTORNOMINAL 10000
// temp. for nominal resistance (almost always 25 C)
#define TEMPERATURENOMINAL 25
// how many samples to take and average, more takes longer
// but is more 'smooth'
#define NUMSAMPLES 5
// The beta coefficient of the thermistor (usually 3000-4000)
#define BCOEFFICIENT 3950
// the value of the 'other' resistor
#define SERIESRESISTOR 10000
Serial.begin(9600);
analogReference(EXTERNAL);
}
uint8_t i;
float average;
for (i=0; i< NUMSAMPLES; i++) {
samples[i] = analogRead(THERMISTORPIN);
delay(10);
}
average = 0;
for (i=0; i< NUMSAMPLES; i++) {
average += samples[i];
}
average /= NUMSAMPLES;
Serial.println(average);
average = 1023 / average - 1;
average = SERIESRESISTOR / average;
Serial.print("Thermistor resistance ");
Serial.println(average);
steinhart = average / THERMISTORNOMINAL; // (R/Ro)
steinhart = log(steinhart); // ln(R/Ro)
steinhart /= BCOEFFICIENT; // 1/B * ln(R/Ro)
steinhart += 1.0 / (TEMPERATURENOMINAL + 273.15); // + (1/To)
steinhart = 1.0 / steinhart; // Invert
steinhart -= 273.15; // convert absolute temp to C
Serial.print(steinhart);
}
int ThermistorPin = 0;int Vo;float R1 = 10000;float logR2, R2, T, Tc, Tf;float c1 = 1.009249522e-03, c2 = 2.378405444e-04, c3 = 2.019202697e-07;void setup() {Serial.begin(9600);}void loop() { Vo = analogRead(ThermistorPin); R2 = R1 * (1023.0 / (float)Vo - 1.0); logR2 = log(R2); T = (1.0 / (c1 + c2*logR2 + c3*logR2*logR2*logR2)); Tc = T - 273.15; Tf = (Tc * 9.0)/ 5.0 + 32.0; Serial.print("Temperature: "); Serial.print(Tf); Serial.print(" F; "); Serial.print(Tc); Serial.println(" C"); delay(500);}
#include <LiquidCrystal.h>int ThermistorPin = 0;int Vo;float R1 = 10000;float logR2, R2, T;float c1 = 1.009249522e-03, c2 = 2.378405444e-04, c3 = 2.019202697e-07;LiquidCrystal lcd(12, 11, 5, 4, 3, 2);void setup() {Serial.begin(9600);}void loop() { Vo = analogRead(ThermistorPin); R2 = R1 * (1023.0 / (float)Vo - 1.0); logR2 = log(R2); T = (1.0 / (c1 + c2*logR2 + c3*logR2*logR2*logR2)); T = T - 273.15; T = (T * 9.0)/ 5.0 + 32.0; lcd.print("Temp = "); lcd.print(T); lcd.print(" F"); delay(500); lcd.clear();}Arduino/Thermistor/Thermistor.ino
/************************************
*name:thermistor
* function:youcan see current temperature displayed on the serial monitor.
**************************************
/Email: [email protected]
//Website: www.primerobotics.in
#define analogPin A0 //the thermistor attach to
#define beta 3950 //the beta of the thermistor
#define resistance 10 //the value of the pull-downresistor
void setup()
{
Serial.begin(9600);
}
void loop()
{
//readthermistor value
long a =analogRead(analogPin);
//thecalculating formula of temperature
float tempC =beta /(log((1025.0 * 10 / a - 10) / 10) + beta / 298.0) - 273.0;
//float tempF= 1.8*tempC + 32.0;//convert centigrade to Fahrenheit
Serial.print("TempC: ");//print" TempC: "
Serial.print(tempC);//print Celsius temperature
Serial.print(" C");//printthe unit
Serial.println();
//Serial.print("TempF: ");
//Serial.print(tempF);
//Serial.print(" F");
delay(200);//wait for 200 milliseconds
}
| * name:thermistor |
| * function:you can see current temperature displayed on the serial monitor. |
| **************************************/ |
| //Email: [email protected] |
| //Website: www.primerobotics.in |
|
|
| #define analogPin A0 //the thermistor attach to |
| #define beta 3950 //the beta of the thermistor |
| #define resistance 10 //the value of the pull-down resistor |
|
|
| void setup() |
| { |
| Serial.begin(9600); |
| } |
|
|
| void loop() |
| { |
| //read thermistor value |
| long a = analogRead(analogPin); |
| //the calculating formula of temperature |
| float tempC = beta /(log((1025.0 * 10 / a - 10) / 10) + beta / 298.0) - 273.0; |
| //float tempF = 1.8*tempC + 32.0;//convert centigrade to Fahrenheit |
| Serial.print("TempC: ");//print" TempC: " |
| Serial.print(tempC);//print Celsius temperature |
| Serial.print(" C");//print the unit |
| Serial.println(); |
| //Serial.print("TempF: "); |
| // Serial.print(tempF); |
| // Serial.print(" F"); |
| delay(200); //wait for 200 milliseconds |
|
Download the code from https://github.com/primerobotics/Arduino |
Posted by Scott Campbell | Arduino | 120
#include <LiquidCrystal.h>int ThermistorPin = 0;int Vo;float R1 = 10000;float logR2, R2, T;float c1 = 1.009249522e-03, c2 = 2.378405444e-04, c3 = 2.019202697e-07;LiquidCrystal lcd(12, 11, 5, 4, 3, 2);void setup() {Serial.begin(9600);}void loop() { Vo = analogRead(ThermistorPin); R2 = R1 * (1023.0 / (float)Vo - 1.0); logR2 = log(R2); T = (1.0 / (c1 + c2*logR2 + c3*logR2*logR2*logR2)); T = T - 273.15; T = (T * 9.0)/ 5.0 + 32.0; lcd.print("Temp = "); lcd.print(T); lcd.print(" F"); delay(500); lcd.clear();}Der Beispielcode für das Arduino Board liest den analogen Input ein.
Der Wert wird in einer Schleife alle 500 Millisekunden neu eingelesen, berechnet und wieder ausgegeben.
Fazit - NTC Temperatur Widerstand
Ein großer Vorteil von temperaturabhängigen Widerständen ist, dass für die Mikrocontroller keine Library oder komplizierte Software benötigt wird.
Das spart Speicher und ist vor allem auch für Anfänger ein guter Einstieg in die Sensorik.
Der NTC hat aber auch einige kleine Nachteile: Da der Sensor analog ist, sollte er immer mit einem anderen genauen Temperatursensor abgeglichen werden.
Bei unseren Tests stellten wir fest, dass die Genauigkeit bei +/- 1,6 Grad liegt.
Für exakte Messungen, wie es zum Beispiel bei einer Wetterstation erwünscht ist, sollte auf diese Art von Sensoren verzichtet werden und ein digitaler Sensor verwendet werden.
Wer nur annähernd einen Temperaturwert ermitteln will, wird mit dieser Lösung sehr zufrieden sein.
Außerdem ist das die wirklich einfachste und günstigste Lösung für eine Temperaturmessung.
In diesem Video zeigen wir, wie man die Temperatur analog und einfach mit einem NTC Widerstand messen kann.
Alle Infos, Schaltplan und den Quellcode gibt es hier:
Quelle:
https://www.aeq-web.com/arduino-measure-temperature-with-ntc-resistor/
https://www.youtube.com/watch?v=6sQWqzwzGgQ
A, B, C, D,
A1, B1, C1, D1 sind konstante Werte je nach Material;
B1=2.56985E-04 0.000256985
C1=2.61013E-06 0.00000261013 0.00000262013
D1=6.38309e-08 0.0000000638309
Rref=10000
R=10000
Thermistoren sind Halbleiter- Widerstände. Ihr Widerstand hängt von der Umgebungstemperatur ab.
Der NTC
Wie gesagt ist der NTC ein Heißleiter und sein Widerstand sinkt, je höher die Umgebungstemperatur ist.
Viele Hersteller bieten einen Datenblatt an, wo man im bestimmten Abständen den Widerstand einer bestimmten Temperatur zuordnen kann.
RN = Der Widerstand bei Nenntemperatur (hier 100kOhm)
B = der angegebene B-Wert vom Hersteller (hier 3950Kelvin)
TN = Die Nenntemperatur in Kelvin ( = 273,15 Kelvin + 25°C = 298,15Kelvin)
T = Die gemessene Temperatur ( den Wert wollen wir haben)
Wir kennen jeden Wert außer Rt. Der ist von der Temperatur abhängig und den müssen wir mit unserem Arduino messen.
Der Spannungsteiler
Der NTC hat bei der Nenntemperatur von 25°C einen Nennwiderstand von 100 Kiloohm.
Die Spannungsteilerregel sagt, dass in einer Reihenschaltung das Verhältnis zwischen Gesamtspannung Uges und Gesamtwiderstand Rges genauso groß ist, wie das Verhältnis zwischen der Spannung UNTC, der an einem Widerstand (hier der NTC) abfällt und sein Widerstandswert RT.
Nun haben wir alles um die Temperatur zu berechnen.
Weiter unten findest du eine Schaltung und einen Beispielsketch mit den man alle wichtigen Werte für den NTC auf den seriellen Monitor darstellen kann.
Was benötigst du?
1x Arduino
1x Steckbrett
1x Widerstand (100kOhm)
1x NTC(Nennwiderstand100kOhm und B-Wert 3950Kelvin)
Jumperkabel (männlich)
int sensorPin = A0;
int bitwertNTC = 0;
long widerstand1=100000; //Ohm
int bWert =3950; // B- Wert vom NTC
double widerstandNTC =0;
double kelvintemp = 273.15; // 0°Celsius in Kelvin
double Tn=kelvintemp + 25; //Nenntemperatur in Kelvin
double TKelvin = 0; //Die errechnete Isttemperatur
double T = 0; //Die errechnete Isttemperatur
void setup() {
Serial.begin(9600); //Seriellen Monitor auf 9600 eingestellt
void loop() {
if (Serial.available()>0) // Wenn serielle Kommunikation vorhanden
{
Serial.println("Sensormessung: ");
bitwertNTC = analogRead(sensorPin); // lese Analogwert an A0 aus
widerstandNTC = widerstand1*(((double)bitwertNTC/1024)/(1-((double)bitwertNTC/1024)));
// berechne den Widerstandswert vom NTC
TKelvin = 1/((1/Tn)+((double)1/bWert)*log((double)widerstandNTC/widerstand1));
// ermittle die Temperatur in Kelvin
T=TKelvin-kelvintemp; // ermittle die Temperatur in °C
Serial.println("Analog: "); //
Serial.println(bitwertNTC); //
Serial.println("NTC- Widerstand: "); //Gebe die ermittelten Werte aus
Serial.println(widerstandNTC); //
Serial.println("Temperatur: "); //Gebe die ermittelten Werte aus
Serial.println(T); //
delay(1000); // Warte eine Sekunde und mache alles nochmal
}
}
int TMP36 = A0; //Der Sensor soll am analogen Pin A0 angeschlossen werden. Wir nennen den Pin ab jetzt "TMP36"int sensorwert;int temperatur = 0; //Unter der Variablen "temperatur" wird später der Temperaturwert abgespeichert.int t=500; //Der Wert für „t“ gibt im Code die zeitlichen Abstände zwischen den einzelnen Messungen vor.void setup() {Serial.begin(9600); //Im Setup beginnt die serielle Kommunikation, damit die Temperatur an den serial monitor übertragen wird. Über die serielle Kommunikation sendet das Board die Messwerte an den Computer. In der Arduino-Software kann man unter „Werkzeuge“ den „Seriellen Monitor“ starten um die Messwerte zu sehen.}void loop() {sensorwert=analogRead(TMP36); //Auslesen des Sensorwertes.temperatur= map(sensorwert, 0, 410, -50, 150); //Umwandeln des Sensorwertes mit Hilfe des "map" Befehls.delay(t); // Nach jeder Messung ist je eine kleine Pause mit der Dauer „t“ in Millisekunden.Serial.print(temperatur); //Nun wird der Wert „temperatur“ über die serielle Kommunikation an den PC gesendet. Durch öffnen des seriellen Monitors in der Arduino-Software kann die Temperatur abgelesen werden.Serial.println(" Grad Celsius"); // Im seriellen Monitor wird hinter der Temperatur die Einheit eingeblendet.}
https://www.youtube.com/watch?v=tF7w9xnOz3A
67) Wie messe ich die Temperatur mit einem Arduino Uno?
Übungsprojekt mit DHT22 Sensor | Arduino #4
https://www.youtube.com/watch?v=ltnPOVchvn4
68) Arduino Lektion 84: NTC-Widerstand (Heißleiter)
https://draeger-it.blog/arduino-lektion-84-ntc-widerstand-heissleiter/
69) Arduino Lektion 48: Temperatursensor DS18B20
https://draeger-it.blog/arduino-lektion-48-temperatursensor-ds18b20/
http://www.scynd.de/tutorials/arduino-tutorials/5-sensoren/5-1-temperatur-mit-10k%CF%89-ntc.html
71) NTC-Thermistor-Testverfahren für Fahrzeug-Klimaanlage
RT=R25exp[A+B/T+C/T2+D/T3]
Der B-Wert ist der Wärmekoeffizient des Thermistors mit negativem Temperaturkoeffizienten.
Das heißt, der Thermistorchip (eine Halbleiterkeramik) bildet nach dem Hochtemperatur Sintern ein Material mit einem spezifischen spezifischen Widerstand.
Der B-Wert kann berechnet werden, indem der Widerstand bei 25 Grad Celsius und 50 Grad Celsius (oder 85 Grad Celsius) gemessen wird.
Der Temperaturkoeffizient bezieht sich auf die Temperatur für jede Erhöhung um 1 Grad.
Widerstand Temperaturkoeffizient = B-Wert / T ^ 2 (T ist der absolute umzurechnende Temperaturwert).
Berechnungsformel für den NTC-Thermistorwiderstand: Rt = R * EXP (B * (1 / T1-1 / T2)
Beschreibung:
In 1 ist Rt der Thermistor im T1-Temperaturwiderstand;
In 2 ist R der Nennwiderstand des Thermistors bei T2-Umgebungstemperatur;
3, B-Wert ist ein wichtiger Parameter des Thermistors;
4, EXP ist die n-te Potenz von e;
5, wobei sich T1 und T2 auf die K-Grad-Kelvin-Temperatur beziehen, K = 273,15 (absolute Temperatur) + Grad Celsius;
Beschreibung: 1, r ist der Thermistorwiderstand bei t Temperatur;
2, ist der Thermistor bei T bei Raumtemperatur der Nennwiderstand;
3, B-Wert ist ein wichtiger Parameter des Thermistors;
4, EXP ist die n-te Potenz von e;
5, wobei sich t und T auf die K-Grad-Kelvin-Temperatur beziehen, K = 273,15 (absolute Temperatur) + Grad Celsius;
Der NTC-Widerstandswerte für zwei unterschiedliche B-Werte sind (beispielsweise 3435 und 3950):
R = 10 · EXP (3435 (1 / t-1 / 298,15))
R = 10 · EXP (3950 (1 / T - 1 / 298,15))
Unter der Annahme, dass die beiden NTC-Widerstände den gleichen Widerstand haben,
3435 (1 / t - 0,003354) = 3950 (1 / T - 0,003354)
Durch Lösen der Gleichung können zwei Arten von B-Wert-Temperaturumwandlungsrelationen erhalten werden:
NTC-Widerstandswert von 3950 B auf 3435 Temperaturwertumwandlungsalgorithmus:
T = 3950 / (3435 / t + 1,727) = 3950 t / (1,727 t + 3435)
Unter ihnen: Temperatureinheit: ℃, (25 Grad über 3950 Wert ist hoch)
NTC-Widerstandswert von 3950 B auf 3435 Temperaturwertumwandlungsalgorithmus:
T = 3435 / (3950 / T-1,727) = 3435T / (3950-1,727T)
Darunter: Temperatureinheit: ℃ (25 Grad über 3435 Wert ist niedrig
Die elektronischen Produktparameter von Yaxun lauten wie folgt:
MF5A-502F-3470 Modelle des Thermistors
Epoxidgehäuse vom Typ MF5A
502 - Der Nennwiderstand bei Raumtemperatur 25 Grad beträgt 5K
F - Die Toleranz beträgt (Genauigkeit) ± 1%
3470 - NTC-Thermistor mit einem B-Wert von 3470K
RT = 5000 * EXP (3470 * (1 / T1-1 / (273,15 + 25)), R = 5000, T2 = 273,15 + 25, B = 3470,
double Thermister(int RawADC) {
double Temp;
Temp = log(((10240000/RawADC) - 10000));
Temp = 1 / (0.001129148 + (0.000234125 +
(0.0000000876741 * Temp * Temp ))* Temp );
Temp = Temp - 273.15;
return Temp;
}
void setup() {
Serial.begin(9600);
}
void loop(){
Serial.print(Thermister(analogRead(0)));
Serial.println("c");
delay(1000);
}
https://docplayer.org/142649812-Xvi-temperaturanzeige-und-simulation-1.html
-
ilm1-2011200608.pdf
76) Physikalische Trainingsaufgaben
Das Dokument Trainingsaufgaben.pdf enthält Übungsaufgaben mit Lösungen für meine Schülerinnen und Schüler.Die Aufgabensammlung deckt noch nicht alle Gebiete ab respektive mit genügend einfachen Aufgaben ab.
M. Lieberherr
Zufällig bin ich in "The Physics Teacher", Feb. 2008, auf die Steinhart-Hart Gleichung zur Beschreibung eines Thermistors gestossen:
1
- = a + b ln R + c (ln R)3
T
Beide Gleichungen gestatten es, aus dem Widerstand die Temperatur zu bestimmen.
Temperatur- und Widerstandsmessungen sind einfach und Thermistoren sind billig.
Deshalb plante ich ein Schüler-Praktikum über Thermistoren, wo Regressionen und grafische Darstellungen geübt werden.
Ich beschaffte mir Thermistoren
EPCOS B57164-K0103 NTC Widerstand, 10k Ohm, 450 mW, 3%
Regressionswerte:
A = 0.001330994
B = 0.000202752
C = 1.57523954E-06
D = 2.81255310E-08 0.00000018094767184
https://www.thinksrs.com/downloads/pdfs/applicationnotes/LDC Note 4 NTC Calculator.pdf
2. Vorwiderstand 100KOhm anschließen lt. Schaltplan. Achtung, da die 24V.Spannung als Referenzspannung dient, sollte sie auch möglichst genau 24V sein. Überprüfen!
3. Mit der NTC-Werteliste und dem nachfolgendem Excel-Berechnungsprogramm die Parameter der Geradengleichungen berechnen.
5. WebUI-Programm erstellen, wobei der Messwert z.B. alle 3 Minuten berechnet wird. (Zeitabstände möglichst groß, um di CCU nicht zu sehr zu belasten!)
Die Auflösung in den einzelnen Arbeitsbereichen ist unterschiedlich.
Die Genauigkeit ist schwieriger abschätzbar.
Anmerken möchte ich noch, daß diese Methode natürlich auch bei anderen nichtlinearen Sensoren
Der Thermistor ist ein elektronisches Temperaturer fassungsgerät, dessen Widerstand sich mit relativen Temperaturänderungen ändert.
Für Temperaturmess- und Steuerungs anwendungen werden normalerweise NTC-Geräte (Negative Temperature Coefficient) verwendet.
Diese sind sehr nützlich für Projekte, die an einen Mikrocontroller angeschlossen sind.
1. Temperatur-Widerstandskurve
Geben Sie drei Datensätze gemäß den tatsächlichen Daten (R1, T1), (R2, T2) und (R3, T3) ein, die unter verschiedenen Temperatur bedingungen gemessen werden müssen.
2. Berechnen Sie den Temperaturkoeffizienten des Steinhart-Hart-Modus
Der Steinhart-Hart-Temperaturkoeffizient des Thermistors kann den Wert von A, B, C über die obigen 3 Temperaturpunkte berechnen.
3. Berechnen Sie den Temperatur koeffizienten des B-Werts
Der B-Wert wird basierend auf den obigen Angaben (R1, T1) und (T2, R2) berechnet.
Anleitung
Geben Sie den Widerstandswert und den Wert von 25 Grad ein, stellen Sie den Schritt zur Berechnung des Widerstandswerts bei jeder Temperatur ein und das Ergebnis kann als Datei exportiert werden.
Berechnungsformel für die NTC-Thermistortemperatur
Rt = R * EXP (B * (1 / T1-1 / T2))
Hier beziehen sich T1 und T2 auf K Grad, dh Kelvin-Temperatur, K Grad = 273,15 (absolute Temperatur) + Grad Celsius, wobei T2 = (273,15 + 25)
Rt ist der Widerstandswert des Thermistors bei der Temperatur T1;
R ist der Nennwiderstand des Thermistors bei normaler Temperatur T2;
Der B-Wert ist ein wichtiger Parameter des Thermistors;
EXP ist die n-te Potenz von e;
Finden Sie T1 = ln (Rt / R) / B + 1 / T2
#include "math.h"
const float Rp=10000.0; //10K
const float T2 = (273.15+25.0);;//T2
const float Bx = 3950.0;//B
const float Ka = 273.15;
float Get_Temp(void)
{
float Rt;
float temp;
Rt = Get_TempResistor();
//like this R=5000, T2=273.15+25,B=3470, RT=5000*EXP(3470*(1/T1-1/(273.15+25)),
temp = Rt/Rp;
temp = log(temp);//ln(Rt/Rp)
temp/=Bx;//ln(Rt/Rp)/B
temp+=(1/T2);
temp = 1/(temp);
temp-=Ka;
return temp;
}
thermistor.sourceforge.net
https://en.wikipedia.org/wiki/Thermistor
//TMP36 Pin Variableint sensorPin = A0; // Analoger Eingangspin, an welchem der TMP36 angeschlossen ist // Die Auflösung beträgt 10 mV / Grad Celsius bei // 500 mV Offset um das Messen negativer Temperaturen zu ermöglichenvoid setup(){ Serial.begin(9600); // Start des seriellen Monitors}void loop() { int reading = analogRead(sensorPin); // Den Signalausgang des Temperatursensors lesen float voltage = reading * 5.0; // Umwandlung der Messung in mV voltage /= 1024.0; Serial.print("Gemessene Spannung: "); Serial.print(voltage); // Ausgabe der gemessenen Spannung in mV Serial.print(" mV;\t"); float temperatureC = (voltage - 0.5) * 100 ; // Umrechnung der Spannung in C° Serial.print("Gemessene Temperatur: "); Serial.print(temperatureC); // Ausgabe der berechneten Temperatur in °C Serial.println(" °C"); delay(1000); // 1 Sekunde warten bis zur nächsten Messung}
#include <math.h> const int sensorPin = A0; // Analoger Eingangspin, an welchem der Thermistor angeschlossen istconst float ThermistorResistance = 10000; // Thermistor Widerstand bei Raumtemperaturconst float NominalTemperature = 25; // Raumtemperaturconst float BCoefficient = 3950; // Beta-Wert des thermistors (aus dem Datenblatt)const float Vsupply = 4.402; // Versorgungspannung des Spannungsteilers (Mit dem Multimeter messen)const float Vref = 4.402; // Analogue Referenzspannung (Mit dem Multimeter messen)const float Rtop = 10000; // Widerstand R1 des Spannungsteilers float MeasureTemperature(){ int nRawThermistor = analogRead(sensorPin); // Messwert aufnehmen float Vout = (float)nRawThermistor * Vref/1023.0; // Berechnung der Ausgangsspannung in Abhängigkeit von der Temperatur float Temp = Vout/Vsupply; // Berechnung des Thermisterwiderstands float Rtherm = Rtop*Temp/(1-Temp); // Umrechnung des Widerstandes des Thermistors in Temperatur über die Steinhart Gleichung float Temperature; Temperature = Rtherm / ThermistorResistance; Temperature = log(Temperature); Temperature /= BCoefficient; Temperature += 1.0 / (NominalTemperature + 273.15); Temperature = 1.0 / Temperature; Temperature -= 273.15; // Umrechnung von Kelvin In Celsius return Temperature;} void setup() { Serial.begin(9600);} void loop() { double temp = MeasureTemperature(); Serial.println(temp); // display tempature delay(500);}
86) Hohe Temperaturen bis 1000°C mit dem MAX6675 und einem Thermoelement vom Typ-K mit dem Arduino messen
// Beispiel Arduino MAX6675 Sketch#include "max6675.h"int ktcSO = 5;int ktcCS = 6;int ktcCLK = 7;MAX6675 ktc(ktcCLK, ktcCS, ktcSO); void setup() { Serial.begin(9600); delay(500); // Zeit für den MAX6675}void loop() { // Einfache Ausgabe auf der seriellen Schnittstelle Serial.print("Temperatur in C = "); Serial.print(ktc.readCelsius()); Serial.print("\t Temperatur in F = "); Serial.println(ktc.readFahrenheit()); delay(500);}
#include <dht.h>#define dataPin 2 // Digitaler-IO, an welchem der Sensor mit dem Arduino verbunden istdht DHT; // Erstellung eines Sensorobjektesvoid setup() { Serial.begin(9600); // Initialisierung der Seriellen Schnittstelle}void loop() { int readData = DHT.read22(dataPin); // Lesen der Sensordaten float t = DHT.temperature; // Zwischenspeichern der Temperaturdaten float h = DHT.humidity; // Zwischenspeichern der gemessenen Feuchtigkeit // Ausgabe der Messung im seriellen Terminal Serial.print("Temperatur = "); Serial.print(t); Serial.print(" °C "); Serial.print(" Feuchtigkeit = "); Serial.print(h); Serial.println(" % "); delay(2000); // Pause für 2 Sekunden, da der DHT22 eine Aufnahmerate von 0,5 Hz besitzt}
88) Präzise analoge Spannungsmessungen mit dem Arduino anhand einer Referenzspannung messen
void setup() { // initialisierung der seriellen Kommunikationsschnittstelle mit 9600 bits pro Sekunde Serial.begin(9600);}// Hauptschleife, welche endlos ausgeführt wird void loop() { // Lesen des Eingangs am analogen Pin A0: int sensorValue = analogRead(A0); // Umrechnung des Analogwertes (welcher von 0 bis 1023 reicht) in eine Spannung von (0V bis 5V): float voltage = sensorValue * (5.0 / 1023.0); // Ausgabe des Wertes über die serielle Schnittstelle Serial.println(voltage);
Filter:
- Mittelwertbildung
float AverageTemperature = 0;int MeasurementsToAverage = 16; // Anzahl der in den Mettelwert aufgenommenen Messungen for(int i = 0; i < MeasurementsToAverage; ++i){ AverageTemperature += MeasureTemperature(); delay(1);}AverageTemperature /= MeasurementsToAverage;
- Mitlaufender Mittelwer
const int RunningAverageCount = 16; // Anzahl der in den Laufenden-Mettelwert aufgenommenen Messungenfloat RunningAverageBuffer[RunningAverageCount];int NextRunningAverage; void loop(){ float RawTemperature = MeasureTemperature(); RunningAverageBuffer[NextRunningAverage++] = RawTemperature; if (NextRunningAverage >= RunningAverageCount) { NextRunningAverage = 0; } float RunningAverageTemperature = 0; for(int i=0; i< RunningAverageCount; ++i) { RunningAverageTemperature += RunningAverageBuffer[i]; } RunningAverageTemperature /= RunningAverageCount; delay(100);}
- Expotentialfilter
#include "Filter.h" ExponentialFilter ExpFilter(20, 0); // Erstellung des Filters mit der Gewichtung 20 und dem Initial-Wert 0 loop{ float RawTemperature = MeasureTemperature(); Exp.Filter(RawTemperature); float SmoothTemperature = Exp.Current(); Serial.print(RawTemperature); // Roh-Wert ausgeben Serial.print(" "); // leerzeichen Serial.println(SmoothTemperature); // Gefilterten Wert ausgeben}
int sensorPin = A0; // Analoger Eingang für die Messleitungint sensorValue = 0; // Variable zur Aufnahme des Messwertes vom Sensor void setup() { Serial.begin(9600); //Initialisierung des seriellen Port mit einer Boudrate von:9600 } void loop() { sensorValue = analogRead(sensorPin); //Liest den Messwert vom Sensor delay(1000); Serial.print("Messwert = " ); Serial.println(sensorValue);}
// I2C Scanner#include <Wire.h>void setup() { Serial.begin (9600); while (!Serial) { } Serial.println (); Serial.println ("Start des I2C scannings..."); byte count = 0; Wire.begin(); for (byte i = 8; i < 120; i++) { Wire.beginTransmission (i); if (Wire.endTransmission () == 0) { Serial.print ("Gefundene Adresse: "); Serial.print (i, DEC); Serial.print (" (0x"); Serial.print (i, HEX); Serial.println (")"); count++; } } Serial.println ("Fertig."); Serial.print ("Anzahl gefundene Module: "); Serial.println (count, DEC);} void loop() {}
2. Das Programm zur Berechnung des Thermistorwiderstandes
Das erste Programm, das wir schreiben, berechnet den Thermistorwiderstand in Ohm.
#define SERIAL_R 102000 // Widerstand des Vorwiderstands, 102 kΩ const byte tempPin = A0; void setup () (Serial.begin (9600); pinMode (tempPin, INPUT);) void loop () (int t = analogRead (tempPin); float tr = 1023.0 / t - 1; tr = SERIAL_R / tr; Serial. println (tr); delay (100);)
Das Ergebnis des Programms:
Möglicherweise stellen Sie fest, dass der gemessene Widerstand des Thermistors weniger als 100 kΩ beträgt, was bedeutet, dass die Umgebungstemperatur unter 25 ° C liegt. Der nächste Schritt ist die Berechnung der Temperatur in Grad Celsius.
3. Das Programm zur Berechnung der Temperatur am Thermistor
Um den Wert der Temperatur mit der Formel Steinhart - Hart zu berechnen:
Die Gleichung enthält die Parameter A, B und C, die aus der Spezifikation zum Sensor entnommen werden müssen.
In dieser Gleichung bleibt nur der Parameter B unbekannt, der für den NTC-Thermistor gleich 3950 ist. Die übrigen Parameter sind uns bereits bekannt:
- T0 ist die Raumtemperatur in Kelvin, für die die Thermistorleistung angegeben ist; T0 = 25 + 273,15;
- T ist die gewünschte Temperatur in Kelvin;
- R ist der gemessene Widerstand des Thermistors in Ohm;
- R0 ist der Nennwiderstand des Thermistors in Ohm.
Wir modifizieren das Programm für Arduino durch Hinzufügen der Temperaturberechnung:
#define B 3950 // B-Koeffizient #define SERIAL_R 102000 // Widerstand des Vorwiderstands, 102 kOhm Byte tempPin = A0; void setup () (Serial.begin (9600); pinMode (tempPin, INPUT);) void loop () (int t = analogRead (tempPin); float tr = 1023.0 / t - 1; tr = SERIAL_R / tr; Serial. print ("R ="); Serial.print (tr); Serial.print (", t ="); float steinhart; steinhart = tr / THERMISTOR_R; // (R / Ro) steinhart = log (steinhart); / / ln (R / Ro) steinhart / = B; // 1 / B * ln (R / Ro) steinhart + = 1.0 / (NOMINAL_T + 273.15); // + (1 / To) steinhart = 1.0 / steinhart; / / Steinhart invertieren - = 273,15; Serial.println (Steinhart); Delay (100);)
Ergebnis:
Schon besser! Das Programm zeigt uns die Temperatur in Grad Celsius. Sie liegt erwartungsgemäß leicht unter 25 ° C.
https://female-page.ru/de/useful-purchase/scheme-and-operating-principle-of-the-thermistor-thermistors.html
https://female-page.ru/de/useful-purchase/modern-methods-of-measuring-temperature-measurement-of-surface-temperature.html
Die wichtigsten Leistungsparameter von Thermistoren sind unter anderem :
- Nennwiderstand bei 25°C. Thermistoren werden in den Auswahlhandbüchern der Hersteller zunächst nach ihrem Nennwert bei dieser Temperatur kategorisiert.
Sie können mit vielen verschiedenen Widerstandswerten bei dieser Temperatur durch Variation ihrer spezifischen Zusammensetzung hergestellt werden.
- Empfindlichkeit, die eine detailliertere Darstellung des Temperaturkoeffizienten darstellt.
Ein niedriger Empfindlichkeitswert kann die Genauigkeit der Temperaturmessungen beeinträchtigen.
Der Temperaturkoeffizient Alpha (α, oder A) ist definiert als die Steigung der Widerstandskurve (R) in Abhängigkeit von der Temperatur an einem bestimmten Punkt und wird mit Gleichung 1 berechnet: Gleichung 1
wobei α in % pro °C angegeben ist.
Alpha selbst ist jedoch nicht konstant, sondern eine Funktion davon, wo sich der Thermistor auf der Kurve befindet.
Um ihn besser zu charakterisieren, hat die Industrie einen weiteren konstanten Faktor Beta (β oder B) definiert, der als Sensitivitätsindex oder Konstante des verwendeten Materials bezeichnet wird.
β wird verwendet, um eine genauere Kurve des Widerstands über der Temperatur zu entwickeln, und eine Spezifikation wie "3380 25/50" gibt eine β Konstante von 3380 über einen Temperaturbereich von 25°C bis 50°C an.
- Weitere Parameter sind die thermische Zeitkonstante (TTC),
Beispielsweise kann die Korrektur von Messwerten für NTC-Thermistoren mit der klassischen Steinhart-Hart-Gleichung durchgeführt werden, einer Kurvenanpassungsgleichung, die die R-T-Kurve des Thermistors, die in Gleichung 5 dargestellt ist, genau wiedergibt:
Gleichung 5Dabei ist T die Temperatur in Kelvin, R ist der berechnete Widerstandswert, A, B und C sind berechnete Koeffizienten, die vom Konstrukteur bestimmt oder vom Thermistorhersteller bereitgestellt werden; dies wird aus offensichtlichen Gründen als "Dreipunktkalibrierung" bezeichnet.
https://www.digikey.at/de/articles/how-to-accurately-sense-temperature-using-thermistors
https://de.wikipedia.org/wiki/Heißleiter
Die Theorie hinter dem Projekt
In der Regel möchten Sie bei Anwendungen, die einen Widerstand verwenden, vermeiden, dass sich der Widerstand bei Temperaturänderungen ändert.
Ein Thermistor kann leicht auf verschiedene Bereiche zugeschnitten werden, je nachdem, welchen Sie kaufen.
Ansatz Drei
/*
================================================================================
File........... Thermistor_Demo_Code
Purpose........ Thermistor demonstration code
Author......... Joseph Corleto
E-mail......... corleto.joseph@gmail.com
Started........ 7/25/2016
Finished....... 7/25/2016
Updated........ --/--/----
================================================================================
Notes
================================================================================
================================================================================
Updates
================================================================================
*/
//===============================================================================
// Header Files
//===============================================================================
//===============================================================================
// Constants
//===============================================================================
//Thermistor related:
/* Here we have a few constants that make editing the code easier. I will go
through them one by one.
A reading from the ADC might give one value at one sample and then a little
different the next time around. To eliminate noisy readings, we can sample
the ADC pin a few times and then average the samples to get something more
solid. This constant is utilized in the readThermistor function.
*/
const int SAMPLE_NUMBER = 10;
/* In order to use the Beta equation, we must know our other resistor
within our resistor divider. If you are using something with large tolerance,
like at 5% or even 1%, measure it and place your result here in ohms. */
const double BALANCE_RESISTOR = 9710.0;
// This helps calculate the thermistor's resistance (check article for details).
const double MAX_ADC = 1023.0;
/* This is thermistor dependent and it should be in the datasheet, or refer to the
article for how to calculate it using the Beta equation.
I had to do this, but I would try to get a thermistor with a known
beta if you want to avoid empirical calculations. */
const double BETA = 3974.0;
/* This is also needed for the conversion equation as "typical" room temperature
is needed as an input. */
const double ROOM_TEMP = 298.15; // room temperature in Kelvin
/* Thermistors will have a typical resistance at room temperature so write this
down here. Again, needed for conversion equations. */
const double RESISTOR_ROOM_TEMP = 10000.0;
//===============================================================================
// Variables
//===============================================================================
// Here is where we will save the current temperature
double currentTemperature = 0;
//===============================================================================
// Pin Declarations
//===============================================================================
//Inputs:
int thermistorPin = 0; // Where the ADC samples the resistor divider's output
//Outputs:
//===============================================================================
// Initialization
//===============================================================================
void setup()
{
// Set the port speed for serial window messages
Serial.begin(9600);
}
//===============================================================================
// Main
//===============================================================================
void loop()
{
/* The main loop is pretty simple, it prints what the temperature is in the
serial window. The heart of the program is within the readThermistor
function. */
currentTemperature = readThermistor();
delay(3000);
/* Here is how you can act upon a temperature that is too hot,
too cold or just right. */
if (currentTemperature > 21.0 && currentTemperature < 24.0)
{
Serial.print("It is ");
Serial.print(currentTemperature);
Serial.println("C. Ahhh, very nice temperature.");
}
else if (currentTemperature >= 24.0)
{
Serial.print("It is ");
Serial.print(currentTemperature);
Serial.println("C. I feel like a hot tamale!");
}
else
{
Serial.print("It is ");
Serial.print(currentTemperature);
Serial.println("C. Brrrrrr, it's COLD!");
}
}
//===============================================================================
// Functions
//===============================================================================
/////////////////////////////
////// readThermistor ///////
/////////////////////////////
/*
This function reads the analog pin as shown below. Converts voltage signal
to a digital representation with analog to digital conversion. However, this is
done multiple times so that we can average it to eliminate measurement errors.
This averaged number is then used to calculate the resistance of the thermistor.
After this, the resistance is used to calculate the temperature of the
thermistor. Finally, the temperature is converted to celsius. Please refer to
the allaboutcircuits.com article for the specifics and general theory of this
process.
Quick Schematic in case you are too lazy to look at the site :P
(Ground) ----\/\/\/-------|-------\/\/\/---- V_supply
R_balance | R_thermistor
|
Analog Pin
*/
double readThermistor()
{
// variables that live in this function
double rThermistor = 0; // Holds thermistor resistance value
double tKelvin = 0; // Holds calculated temperature
double tCelsius = 0; // Hold temperature in celsius
double adcAverage = 0; // Holds the average voltage measurement
int adcSamples[SAMPLE_NUMBER]; // Array to hold each voltage measurement
/* Calculate thermistor's average resistance:
As mentioned in the top of the code, we will sample the ADC pin a few times
to get a bunch of samples. A slight delay is added to properly have the
analogRead function sample properly */
for (int i = 0; i < SAMPLE_NUMBER; i++)
{
adcSamples[i] = analogRead(thermistorPin); // read from pin and store
delay(10); // wait 10 milliseconds
}
/* Then, we will simply average all of those samples up for a "stiffer"
measurement. */
for (int i = 0; i < SAMPLE_NUMBER; i++)
{
adcAverage += adcSamples[i]; // add all samples up . . .
}
adcAverage /= SAMPLE_NUMBER; // . . . average it w/ divide
/* Here we calculate the thermistor’s resistance using the equation
discussed in the article. */
rThermistor = BALANCE_RESISTOR * ( (MAX_ADC / adcAverage) - 1);
/* Here is where the Beta equation is used, but it is different
from what the article describes. Don't worry! It has been rearranged
algebraically to give a "better" looking formula. I encourage you
to try to manipulate the equation from the article yourself to get
better at algebra. And if not, just use what is shown here and take it
for granted or input the formula directly from the article, exactly
as it is shown. Either way will work! */
tKelvin = (BETA * ROOM_TEMP) /
(BETA + (ROOM_TEMP * log(rThermistor / RESISTOR_ROOM_TEMP)));
/* I will use the units of Celsius to indicate temperature. I did this
just so I can see the typical room temperature, which is 25 degrees
Celsius, when I first try the program out. I prefer Fahrenheit, but
I leave it up to you to either change this function, or create
another function which converts between the two units. */
tCelsius = tKelvin - 273.15; // convert kelvin to celsius
return tCelsius; // Return the temperature in Celsius
}
Messen der Temperatur mit einem NTC-Thermistor
Erfahren Sie mehr über Thermistoren und wie Sie einen Arduino programmieren, um seine Daten zu messen.
Haben Sie sich jemals gefragt, wie manche Geräte wie Thermostate, 3D-Drucker, Wärmebetten, Automotoren oder Öfen Temperatur messen?
Stückliste
Hardware
Arduino
MEGA oder Uno oder dein Lieblingsaroma von Arduino
Einige Schaltdrähte
Löt- und Lötkolben (falls der Thermistor nicht gut in die Arduino-Header passt)
Software
Arduino IDE
Theorie
Bei einer typischen Anwendung eines Widerstands möchten Sie nicht, dass sich der Widerstand mit der Temperatur ändert.
Aber was, wenn Sie wirklich wollten, dass die Helligkeit der LED eine Funktion der Temperatur ist?
Die Einheiten werden angezeigt, aber nicht die tatsächlichen Werte, da ein Thermistor je nach dem, was Sie kaufen, an verschiedene Bereiche angepasst werden kann.
Es gibt auch Thermistoren, die einen positiven Temperaturkoeffizienten (PTC) haben, was bedeutet, dass mit steigender Temperatur der Widerstand zunimmt.
Für den Rest des Artikels können Sie davon ausgehen, dass wir uns auf Thermistoren vom NTC-Typ beziehen.
Vier Ansätze zum Finden einer Kurvenanpassungsformel
Jetzt, da wir das allgemeine Verhalten von Thermistoren besser verstehen, können Sie sich fragen, wie wir möglicherweise ein Arduino zur Temperaturmessung verwenden könnten.
Also was zu tun?
Bevor Sie weiterlesen, denken Sie darüber nach, wie Sie dies in der Arduino oder sogar eine Schaltung ohne eine Mikroprozessorkomponente tun würden.
Es gibt einige Möglichkeiten, wie Sie sich diesem Problem nähern können. Dies ist keineswegs eine Liste aller Techniken, aber es wird Ihnen einige beliebte Ansätze zeigen.
Ansatz eins:
Einige Hersteller sind so nett, Ihnen eine ganze Karte zu geben, die einen bestimmten ganzzahligen Bereich von Temperatur und Widerstand (typische Werte) abbildet.
Aber dann denkst du, wie du das im Arduino machen würdest. Sie müssten alle diese Werte in einer riesigen Nachschlagetabelle oder einer sehr langen Kontrollstruktur "switch … case" oder "if … then" fest codieren.
Und wenn der Hersteller nicht nett genug ist, eine Nachschlagetabelle zu geben, müssen Sie jeden Punkt selbst messen, um die Daten zu generieren.
Aber für unser Projekt möchten wir einen nahezu kontinuierlichen Bereich messen und an den seriellen Monitor senden, so dass diese Methode nicht verwendet wird.
Ansatz zwei:
Sie könnten versuchen, die Antwort vom Thermistor zu "linearisieren", indem Sie eine externe Schaltung hinzufügen.
Ein beliebter Weg, dies zu tun, besteht darin, einen Widerstand parallel zum Thermistor anzuschließen.
Das Bestimmen, wie eine Region ausgewählt und linearisiert wird, sowie das Auswählen des richtigen Wertes ist ein Artikel für sich.
Aber wir haben einen Mikroprozessor in diesem Artikel und wollen den gesamten Bereich nutzen.
Ansatz drei:
Sie könnten die Tabellendaten aus dem Datenblatt nehmen oder (wenn Sie sich gerne selbst bestrafen) Ihre eigenen Daten, die Sie mit unabhängigen Messungen erstellt haben, erstellen und das Diagramm in etwas wie Excel neu erstellen.
Obwohl dies ein legitimer Ansatz ist, wollen wir nicht bei der Analyse all dieser Daten stecken bleiben.
Es stellt sich heraus, dass es eine allgemeine Kurvenanpassungsformel gibt, die für Vorrichtungen wie Thermistoren gedacht ist.
$ \ frac {1} {T} = A + B \ ln (R) + C (\ ln (R)) ^ 3 $$
wobei R der Widerstand des Thermistors bei der Temperatur T (in Kelvin) ist.
Dies ist eine allgemeine Kurvenanpassungsgleichung, um alle NTC-Widerstände aufzunehmen.
Beachten Sie, dass die Gleichung die Konstanten A, B und C benötigt.
Selbst für diejenigen von uns, die algebraische Zauberer sind, ist dies immer noch zu viel Arbeit.
Stattdessen gibt es eine einfachere Gleichung, die weniger genau ist, aber nur eine Konstante hat.
$ \ frac {1} {T} = \ frac {1} {T_o} + (\ frac {1} {\ beta}) \ cdot \ ln \ links (\ frac {R} {R_o} \ right) $ $
Widerstandsmessung mit dem Arduino
Jetzt, wo wir unseren Ansatz aus dem Weg haben, müssen wir herausfinden, wie man den Widerstand mit dem Arduino tatsächlich misst, bevor wir diese Informationen in die β-Gleichung einspeisen können.
In der Regel verwenden wir einen Spannungsteiler mit folgender Gleichung:
\ (V_ {out} = V_ {s} \ cdot (\ frac {R_ {balance}} {R_ {Thermistor} + R_ {balance}}) \)
Aber wir wollen nicht Vout als Antwort - wir wollen Rthermistor. Also lasst uns dafür mit Algebra-Magie lösen:
\ (R_ {Thermistor} = R_ {Gleichgewicht} \ cdot (\ frac {V_s} {V_ {out}} - 1) \)
Das ist fast perfekt, aber wir müssen jetzt unsere Ausgangsspannung sowie die Versorgungsspannung messen.
Wir können die Spannung als eine digitale Zahl in einem bestimmten Maßstab darstellen.
\ (R_ {Thermistor} = R_ {Gleichgewicht} \ cdot (\ frac {D_ {max}} {D_ {gemessen}} - 1) \)
Dies funktioniert mathematisch, denn unabhängig davon, wie wir die Spannung darstellen (in Volt oder in digitalen Einheiten), heben sich diese Einheiten oben und unten in der Fraktion auf und hinterlassen eine dimensionslose Zahl.
D max für uns wird 1023 sein, da dies die höchste von unserem 10-Bit-ADC erzeugte Zahl ist.
Verdrahtung es oben
Ich benutzte einen TH10K Thermistor.
Ich benutzte auch einen 10k Ohm Widerstand für R Balance in unserem Spannungsteiler.
Unten ist ein vollständiges Schema. Es ist eigentlich ziemlich einfach und unkompliziert!
Der Code hier wurde mit viel Nachdenken ausgelegt und hat eine Fülle von Kommentaren, um Ihnen zu helfen, durch die Logik zu kommen.
Im Grunde misst es die Spannung des Teilers, berechnet die Temperatur und zeigt dies dann im seriellen Anschluss an.
Zum Spaß gibt es auch einige "if … then" -Aussagen, die zeigen, wie man auf verschiedene Temperaturen und einen einzelnen Datenpunkt reagieren kann.
Wie immer, kommentieren Sie unten für Fragen!
/*
================================================================================
File........... Thermistor_Demo_Code
Purpose........ Thermistor demonstration code
Author......... Joseph Corleto
E-mail......... corleto.joseph@gmail.com
Started........ 7/25/2016
Finished....... 7/25/2016
Updated........ --/--/----
Mögliche nächste Schritte
Alles in diesem Artikel zeigt eine ziemlich einfache Art der Temperaturmessung mit einem billigen Thermistor.
Setzen Sie einen kleinen Kondensator parallel zur Ausgangsspannung.
Verwenden Sie Präzisionswiderstände (besser als 1%), um eine konsistentere und vorhersagbarere Messung zu erhalten.
Natürlich sind Thermistoren nur ein Sensor für Temperaturmessungen.
Ich hoffe, dies gibt Ihnen eine bessere Idee, wie Sie die Temperatur für Ihr nächstes Projekt messen können!
Thermistorcode
Gib diesem Projekt einen Versuch für dich selbst! Holen Sie sich die Stückliste.
Thorlabs
Electronics-Council.com
https://www.digikey.com/en/maker/projects/how-to-measure-temperature-with-an-ntc-thermistor/4a4b326095f144029df7f2eca589ca54
https://www.digikey.com/en/products/detail/arduino/A000066/2784006
https://www.digikey.com/en/products/detail/adafruit-industries-llc/153/7241430
Ich frage mich, ob es möglich ist, A-, B- und C-Werte für TTF-103Thermistoren aus dem Datenblatt zu extrahieren .
Diese Werte werden zur Berechnung des Widerstands nach der Steinhart-Hart-Gleichung benötigt .
Gegeben für NTC Sernsor TTF3A103F34D: B25/85 = 3435K 103 = 10k NTC F = 1% 34 beta Value First D Beta Value Last
273,15 = 0,00 °C
T1 = 298,15 K - 273,15 = 25,00 °C
T2 = gesuchte Temperatur
Gegeben für NTC Sernsor TTF3A103_34D: 103 = 10k NTC
R2 = R25 / (exp (B * (1 / T1 - 1 / T2)))
| = 10000 / (EXP (3435 * (1 / 298,15 - 1 / (273,15+85)))) | 1451,3 |
| = 10000 / (EXP (3435 * (1 / 298,15 - 1 / (273,15+60)))) | 2980,9 |
| = 10000 / (EXP (3435 * (1 / 298,15 - 1 / (273,15+25)))) | 10000,0 |
| = 10000 / (EXP (3435 * (1 / 298,15 - 1 / (273,15+0)))) | 28704,3 |
Betriebstemperatur von -40 °C bis +125 °C
Erhältlich in den Toleranzklassen ±1 %, ±3 %, ±5 % und ±10 % in Bezug auf den R25 Widerstandswert
Bei der applikationsbezogenen Auswahl von NTC-Thermistoren gibt es neben den üblichen ökonomischen Aspekten eine Reihe von technischen
Kriterien, die für die Bestimmung des passenden NTC-Thermistors von Bedeutung sind.
Nennwiderstand
Der Nennwiderstand (R25) eines NTC-Thermistors bezieht sich stets auf 25 °C.
Maximale Betriebstemperatur
Dieser Begriff beschreibt die maximale Körpertemperatur, bei welcher der Thermistor seine Stabilität und Charakteristik noch aufrecht erhalten kann.
Dissipationsfaktor
Dieser Faktor, auch bekannt als Verlustleistungs-Konstante, bezeichnet die Leistung in mW/°C, die erforderlich ist, um die Thermistor-Körpertemperatur um 1 °C in einem bestimmten Medium (z.B. Luft oder Öl) zu erhöhen.
Der Dissipationsfaktor ist eine wichtige Größe in Anwendungen, welche sich den Eigenerwärmungs- Effekt von NTC-Thermistoren zu Nutze machen,
Maximale Leistungsaufnahme
Dies ist die maximale Leistung (in mW oder W), die ein Thermistor über einen längeren Zeitraum aufnehmen kann, ohne dass dabei die Charakteristik oder die Stabilität des Thermistors beeinträchtigt wird
Thermale Zeitkonstante (T.C.)
T.C. definiert die Zeit in Sekunden, die ein Thermistor benötigt, um bei Null-Leistungsaufnahme eine Temperaturänderung seines Körpers von 63,2 % zwischen Anfangs- und Endtemperartur zu erreichen.
Ein NTC-Thermistor wird in ein 25 °C warmes Ölbad getaucht und verbleibt dort einige Zeit, um sich thermisch zu stabilisieren.
Die Thermale Zeitkonstante ist nun die Zeit, die vergeht, bis der NTC-Thermistor eine Körpertemperatur von 56,6 °C (=63,2 % Temperaturunterschied) erreicht hat.
Der α-Wert bezeichnet den sogenannten Widerstands- Temperaturkoeffizienten als prozentuale Widerstandsänderung pro °C Temperaturänderung.
Temperaturpunkt ermitteln.
Ein Thermistor aus unserer Interchangeable-Serie mit Materialkurve #3 (siehe Seite 130) hat einen Widerstand von RT = 10000 Ohm bei +25 °C.
Slope-Kennlinie
Eine 0°C - 70°C-Slope-Kennlinie ist in vorausgehender Grafik dargestellt.
Der β-Wert bezeichnet die Charakteristik eines NTC-Thermistors in Bezug auf zwei Widerstandswerte,
Die Beta-Wert-Konstante ist ein Maß für die Zusammensetzung des Thermistor-Ausgangsmaterials (gesinterte Metall-Oxide).
/* Temperaturmessung mit einem NTC Thermistor von Thomas Ecker www.physicalcomputing.at Mai 2010 */ #include <math.h> int SensorPin = 0; // Für den Senoreingang wird Analog 0 gewählt float sensorWert = 0; // Variable, die den Sensor Wert annimmt float u1 =0; // Spannung u1 am Spannungsteiler float u2 = 0; // Spannung u2 am Spannungsteiler float i = 0; // Strom in A float Rntc = 0; // Widerstand des Thermistors zum Zeitpunkt der Messung float T = 0; // Variable für gemessene Temperatur float B = 4090; // Wert aus Datenblatt des Thermistors float Tn = 298.16; // Nenntemperatur in K float R25 = 3473; // Nennwiderstand in Ohm bei Nenntemperatur (aus Datenblatt) void setup() { Serial.begin (9600); // Temperatur kann im "Serial Monitor" abgelesen werden } void loop() { sensorWert = analogRead(SensorPin); // Wert am Sensor wird gelesen u2 = (sensorWert * 5)/1024; // Spannung am Sensor wird berechnet u1 = 5-u2; // Spannung am Vorwiderstand wird berechnet i = u1/1000; // Strom wird berechnet Rntc = u2/i; // Widerstand des Thermistors zum Zeitpunkt der Messung T = (B*Tn)/(B+(log(Rntc/R25)*Tn)); // Berechnung der Temperatur T = T-273.15; // Umrechnung von K in °C Serial.print ("Temperatur = "); Serial.print (T); Serial.print (" sensorwert = "); Serial.print (sensorWert); Serial.println (" "); delay (2000); // Temperatur wird alle 2 sec. gemessen }Die geläufigste Näherungsformel lautet
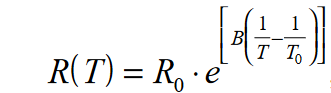
wobei T die Temperatur in Kelvin und R0 der Widerstand bei der Temperatur T0 ist.
Die Definition des Temperaturkoeffizienten lautet wie folgt
Die bestmögliche mathematische Beschreibungsform der Heißleiterkennlinie ist die Gleichung nach Steinhart und Hart.
Zur analogen Weiterverarbeitung des Meßsignals ist es zweckmäßig, die Thermistorkennlinie zu linearisieren, was durch einfache Reihen- oder Parallelschaltung eines Widerstandes zum Sensor erreicht werden kann.
Als Beispiel betrachten wir die Linearisierung einer Heißleiterkennlinie durch Parallelschalten eines Widerstandes.

Versuch 22: Technische Temperaturmessung Seite 13
 mit
mit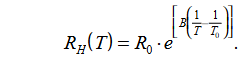
Die Verläufe von RH(delta) und Rg(delta) sind oben dargestellt.
Durch geeignete Dimensionierung des Parallelwiderstands Rp kann man erreichen, daß die Kennlinie in einem bestimmten Temperaturbereich nahezu linear verläuft.
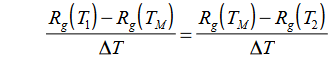
mit

Daraus folgt die Bedingung
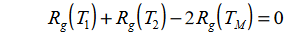
Durch Einsetzen der Ausdrücke für die Parallelschaltung von RH und Rp in diese Gleichung und Freistellen nach Rp erhält man für den Parallelwiderstand Rp die Dimensionierungsgleichung
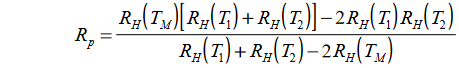
300_d_Meßtechnik-x_Versuch 22 - Technische Temperaturmessung vm22_1a.pdf
R = R25 * e ^ (B * (1/T - 1/T25))
R(T)=A*e^(B/T)
R t1 = Widerstand bei Temperatur 1
R t2 = Widerstand bei Temperatur 2
T1 = Temperatur 1 in (°K)
T2 = Temperatur 2 in (°K)
Die Widerstandskurve entspricht nicht direkt einer e-Funktion
B ist nicht wirklich konstant, sondern von der Temperatur abhängig.
Der Thermistor ist ein Festkörper-Temperatursensor, der ein bisschen wie ein elektrischer Widerstand wirkt, aber temperaturempfindlich ist. Thermistoren können verwendet werden, um eine analoge Ausgangsspannung bei Schwankungen der Umgebungstemperatur zu erzeugen und können als solche als Wandler bezeichnet werden.
Der Thermistor ist im Grunde ein wärmeempfindlicher Festkörperwandler mit zwei Anschlüssen, der unter Verwendung von empfindlichen Metalloxiden auf Halbleiterbasis mit metallisierten oder gesinterten Verbindungsleitungen aufgebaut ist, die zu einer Keramik-Scheibe oder Keramik-Perle geformt sind.
Dadurch kann der Thermistor seinen Widerstandswert proportional zu kleinen Änderungen der Umgebungstemperatur ändern.
Während bei Standardwiderständen die Widerstandsänderung durch Wärme im Allgemeinen unerwünscht ist, kann dieser Effekt in vielen Temperaturerfassungsschaltungen gut genutzt werden.
Als Festkörperbauelement aus hochempfindlichen Metalloxiden arbeiten sie auf molekularer Ebene, wobei die äußersten (Valenz-) Elektronen aktiver werden, was einen negativen Temperaturkoeffizienten erzeugt, oder weniger aktiv, was einen positiven Temperaturkoeffizienten als die Temperatur des Thermistors erzeugt erhöht.
Das heißt, sie haben eine sehr gute Beständigkeit / Temperatureigenschaften so dass sie bei Temperaturen bis zu 200 °C in Einsatz kommen.
Typischer Scheiben-Thermistor
Obwohl Thermistoren hauptsächlich als resistive Temperatursensoren verwendet werden, können sie auch in Reihe mit einem anderen Bauteil oder Gerät geschaltet werden, um einen durch sie fließenden elektrischen Strom zu steuern.
Thermistoren sind in einer ganzen Reihe von Typen, Materialien und Größen erhältlich, die sich durch ihre Ansprechzeit und Betriebstemperatur auszeichnen.
Diese wärmeabhängigen Widerstände können auf zwei Arten arbeiten, entweder durch Erhöhen oder Verringern ihres Widerstandswerts bei Temperaturänderungen.
Negative Temperaturkoeffizienten von Widerstandsthermistoren oder kurz NTC-Thermistoren verringern oder verringern ihren Widerstandswert, wenn die Betriebstemperatur um sie herum steigt.
NTC-Temperaturthermistoren haben eine negative Beziehung zwischen elektrischem Widerstand und Temperatur (R/T).
Wir haben bereits gesagt, dass ein Thermistor ein elektronisches Bauteil ist, dessen Widerstand stark von der Temperatur abhängt.
Ein NTC-Thermistor verringert seinen Widerstand mit steigender Temperatur und ist in einer Vielzahl von Basiswiderständen und Temperaturkurven erhältlich.
Ein weiteres wichtiges Merkmal eines Thermistors ist sein „B“-Wert.
Somit wird die B wird Wert der Thermistoren Widerstandswert bei einer ersten Temperatur oder Fußpunkt definieren,
Daher definiert der B- Wert die Materialkonstante des Thermistors zwischen dem Bereich von T1 und T2.
Beachten Sie jedoch, dass beide Temperaturpunkte von T1 und T2 in den Temperatureinheiten Kelvin berechnet werden
Wenn Sie also den B- Wert eines bestimmten Thermistors kennen (aus dem Datenblatt des Herstellers erhalten), ist es möglich, eine Tabelle der Temperatur gegenüber dem Widerstand zu erstellen, um ein geeignetes Diagramm unter Verwendung der folgenden normalisierten Gleichung zu erstellen:
T2 ist der zweite Temperaturpunkt in Kelvin
R1 ist der Widerstand des Thermistors bei der Temperatur T1 in Ohm
R2 ist der Widerstand des Thermistors bei der Temperatur T2 in Ohm
Ein 10k NTC Thermistor mit einem B-Wert von 3455 zwischen dem Temperaturbereich von 25 °C und 100 °C.
Angegebene Daten:
Der Wert von R1 ist bereits als 10k Ohm Basiswiderstand angegeben, somit berechnet sich der Wert von R2 bei 100 °C wie folgt:
Geben Sie das folgende Zwei-Punkte-Eigenschaftsdiagramm von:

Beachten Sie, dass in diesem einfachen Beispiel nur zwei Punkte gefunden wurden, aber im Allgemeinen ändern Thermistoren ihren Widerstand exponentiell mit Temperaturänderungen, sodass ihre Kennlinie nichtlinear ist.
Temperatur ( ° C) 10 20 25 30 40 50 60 70 80 90 100 110 120
Widerstand (Ω) 18476 12185 10000 8260 5740 4080 2960 2188 1645 1257 973 765 608
und diese Punkte können wie gezeigt aufgetragen werden, um eine genauere Kennlinie für den 10k Ohm NTC-Thermistor mit einem B-Wert von 3455 zu erhalten.

Beachten Sie, dass es einen negativen Temperaturkoeffizienten (NTC) hat,
Wie können wir also einen Thermistor verwenden, um die Temperatur zu messen?

Der einfachste Weg, dies zu tun, besteht darin, den Thermistor wie gezeigt als Teil einer Potenzialteilerschaltung zu verwenden.
Wenn beispielsweise wir einen 10k - Thermistor mit einem Vorwiderstand von 10k zu verwenden, dann ist die Ausgangsspannung an der Basistemperatur von 25 °C wird die Hälfte der Versorgungsspannung sein als 10 Ohm / (10 Ohm + 10 Ohm) = 0,5.
Wenn sich der Widerstand des Thermistors aufgrund von Temperaturänderungen ändert, ändert sich auch der Anteil der Versorgungsspannung am Thermistor, wodurch eine Ausgangsspannung erzeugt wird, die proportional zum Anteil des gesamten Serienwiderstands zwischen den Ausgangsanschlüssen ist.
Somit ist die Potentialteilerschaltung ein Beispiel für einen einfachen Widerstands-Spannungs-Wandler, bei dem der Widerstand des Thermistors durch die Temperatur gesteuert wird, wobei die erzeugte Ausgangsspannung proportional zur Temperatur ist.
Wenn wir die Positionen des Serienwiderstands R S und des Thermistors R TH vertauschen , würde sich die Ausgangsspannung in die entgegengesetzte Richtung ändern, dh je heißer der Thermistor wird, desto höher ist die Ausgangsspannung.

Wir können NTC-Thermistoren als Teil einer grundlegenden Temperaturerfassungskonfiguration verwenden, die eine Brückenschaltung wie gezeigt verwendet.
Wenn sich die Temperatur und damit der Widerstandswert des Thermistors ändert, ändert sich auch die Spannung an V TH , entweder höher oder niedriger als die an V REF, was ein positives oder negatives Ausgangssignal an den angeschlossenen Verstärker erzeugt.
Die für diese grundlegende Temperaturerfassungsbrückenschaltung verwendete Verstärkerschaltung könnte als Differenzverstärker für hohe Empfindlichkeit und Verstärkung oder als einfache Schmitt-Triggerschaltung zum EIN-AUS-Schalten dienen.
Das Problem mit einem Strom , der durch einen Thermistor auf diese Weise verläuft, ist , dass Thermistoren Erfahrung , was eine Eigenerwärmung genannt wird, dass der I 2 * R Leistungsverlust könnte hoch genug sein , um mehr Wärme zu erzeugen , als durch den Thermistor abgeführt werden Beeinflussung seines Widerstandswerts und führt zu falschen Ergebnissen.
Daher ist es möglich, dass ein zu hoher Strom durch den Thermistor zu einer erhöhten Verlustleistung führt und mit steigender Temperatur sein Widerstand abnimmt, wodurch mehr Strom fließt, was die Temperatur weiter erhöht, was zu einem sogenannten Thermal Runaway führt .
Der Wert für den Reihenwiderstand R S oben sollte so gewählt werden, dass er über den erwarteten Temperaturbereich, für den der Thermistor wahrscheinlich verwendet wird, ein angemessen breites Ansprechverhalten bietet, während gleichzeitig der Strom bei der höchsten Temperatur auf einen sicheren Wert begrenzt wird .
Eine Möglichkeit, dies zu verbessern und eine genauere Umwandlung des Widerstands gegenüber der Temperatur (R/T) zu erreichen, besteht darin, den Thermistor mit einer Konstantstromquelle zu betreiben.
Wir haben hier gesehen, dass Thermistoren als resistive temperaturempfindliche Wandler verwendet werden, aber der Widerstand eines Thermistors kann sich entweder durch äußere Temperaturänderungen oder durch Temperaturänderungen, die durch einen durch sie fließenden elektrischen Strom verursacht werden, ändern, da es sich schließlich um ohmsche Geräte handelt .
Das Ohmsche Gesetz sagt uns, dass, wenn ein elektrischer Strom aufgrund der angelegten Spannung durch einen Widerstand R fließt, aufgrund des I 2 * R Heizeffekts Energie in Form von Wärme verbraucht wird .
Induktive elektrische Geräte wie Motoren, Transformatoren, Vorschaltgeräte usw. leiden beim ersten Einschalten unter übermäßigen Einschaltströmen.

Einschaltstromunterdrücker und Überspannungsbegrenzer sind Typen von in Reihe geschalteten Thermistoren, deren Widerstand auf einen sehr niedrigen Wert abfällt, wenn er durch den durch ihn fließenden Laststrom erwärmt wird.
Infolge des Laststroms erwärmt sich der Thermistor und verringert seinen Widerstand relativ langsam bis zu dem Punkt, an dem die Verlustleistung über ihm ausreicht, um seinen niedrigen Widerstandswert beizubehalten, wobei der größte Teil der angelegten Spannung über der Last entwickelt wird.
Aufgrund der thermischen Trägheit seiner Masse dauert dieser Heizeffekt einige Sekunden, während derer der Laststrom allmählich und nicht sofort ansteigt, sodass ein hoher Einschaltstrom begrenzt und die aufgenommene Leistung entsprechend reduziert wird.
Die Ansprechgeschwindigkeit eines strombegrenzenden Thermistors ist durch seine Zeitkonstante gegeben.
NTC-Thermistoren bieten Schutz vor unerwünscht hohen Einschaltströmen, während ihr Widerstand im Dauerbetrieb zur Stromversorgung der Last vernachlässigbar gering bleibt.
Wir haben hier in diesem Tutorial über Thermistoren gesehen, dass ein Thermistor ein zweipoliger Widerstandswandler ist, der seinen Widerstandswert mit Änderungen der Umgebungstemperatur ändern kann, daher der Name Thermowiderstand oder einfach „Thermistor“.
Thermistoren sind kostengünstige, leicht erhältliche Temperatursensoren, die unter Verwendung von Halbleitermetalloxiden aufgebaut sind.
NTC-Thermistoren sind die am häufigsten verwendeten (insbesondere der 10k Ohm NTC-Thermistor) und zusammen mit einem zusätzlichen Vorwiderstand kann RS als Teil einer einfachen Potenzialteilerschaltung verwendet werden.
Der Betriebsstrom des Thermistors muss jedoch so gering wie möglich gehalten werden, um eventuelle Eigenerwärmungseffekte zu reduzieren.
Thermistoren zeichnen sich durch ihren Basiswiderstand sowie ihren „B“-Wert aus.
Wir haben auch gesehen, dass Thermistoren nicht nur zur Messung einer Außentemperatur verwendet werden, sondern auch zur Steuerung eines elektrischen Stroms aufgrund des I 2 R Heizeffekts, der durch den durchfließenden Strom verursacht wird.
ENDE


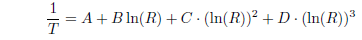
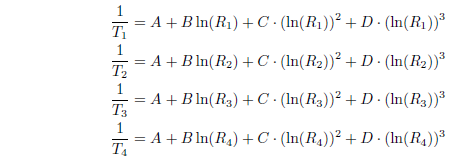


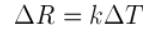

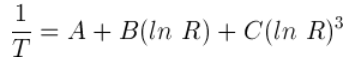




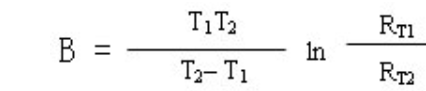

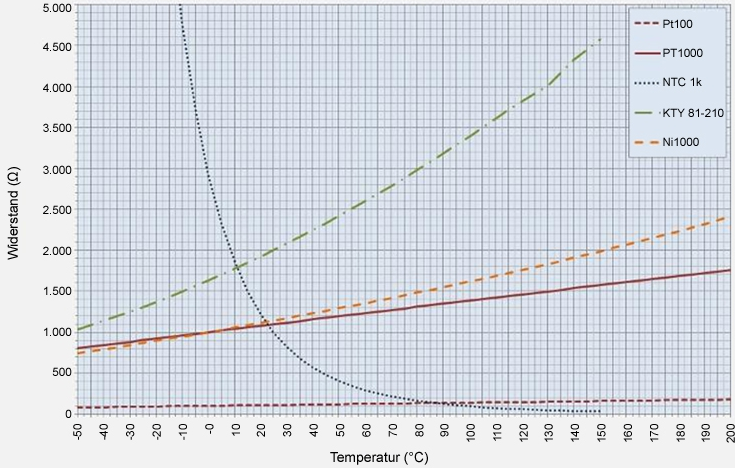





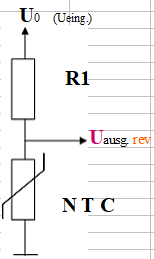






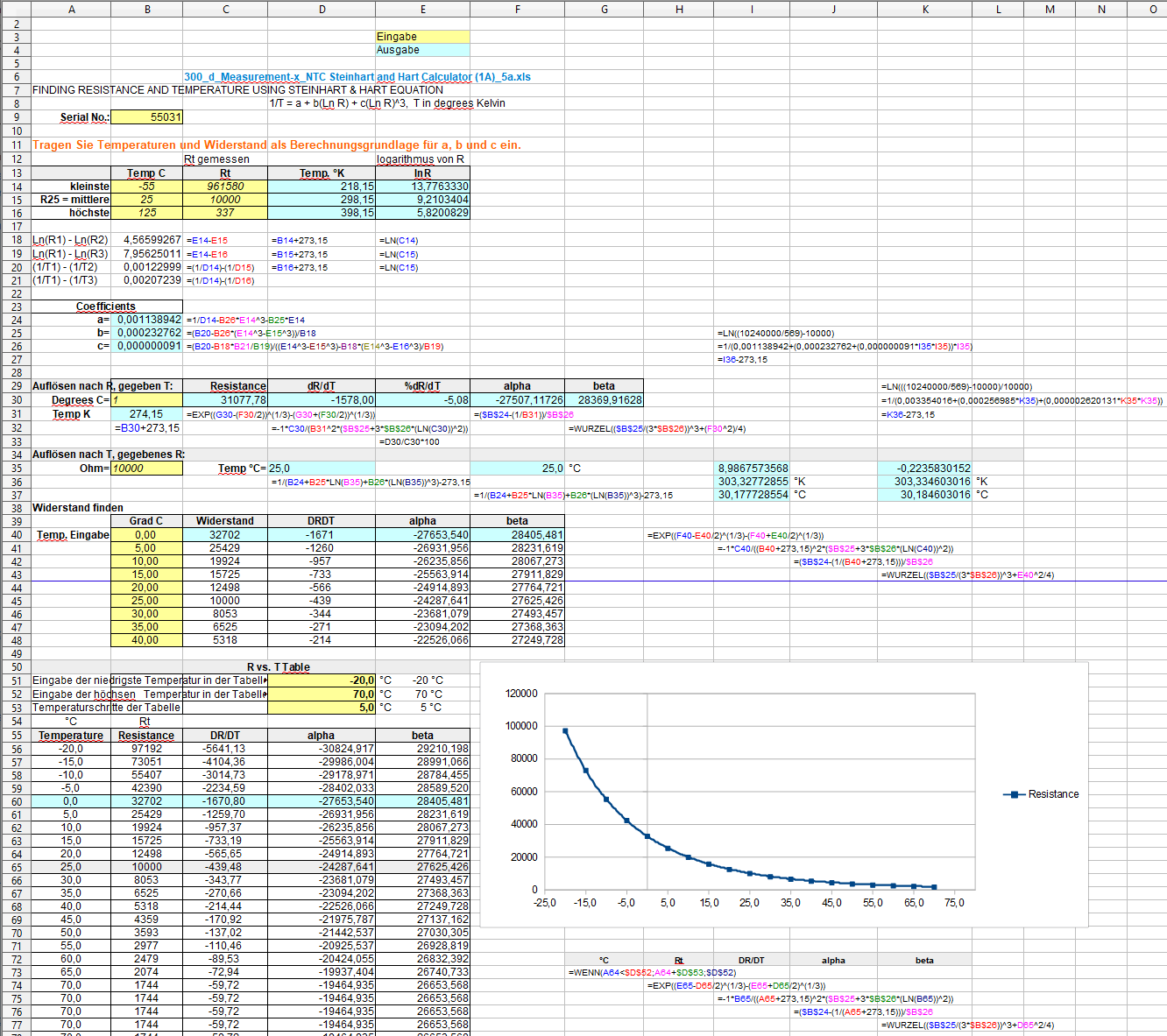
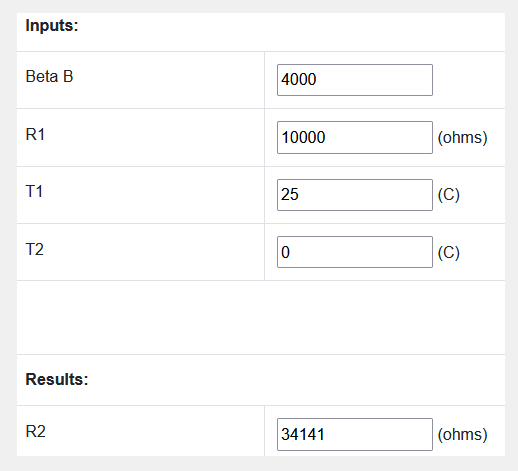



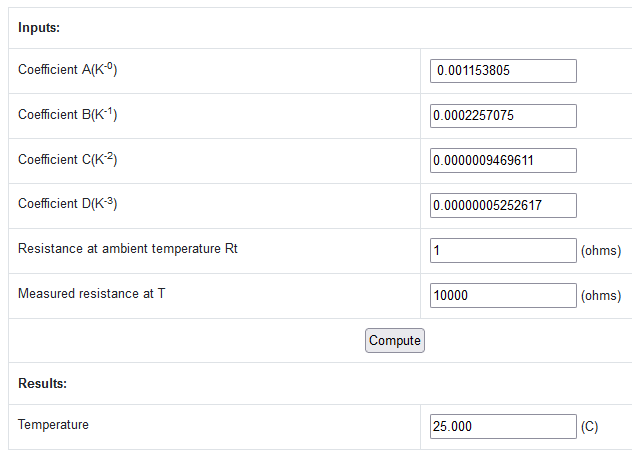





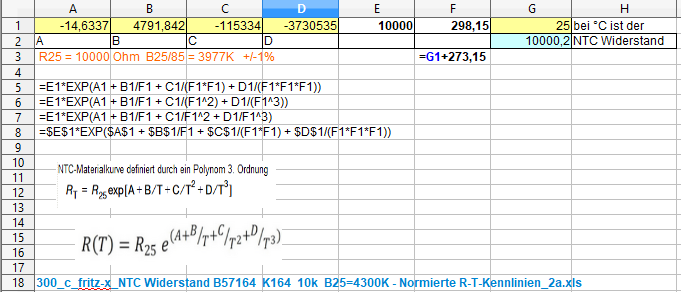
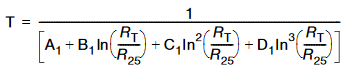










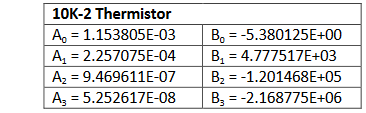



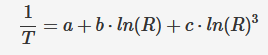
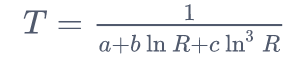





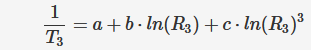



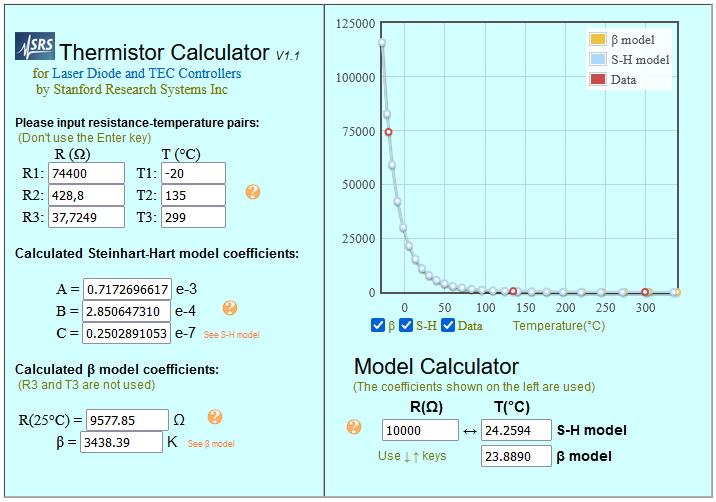
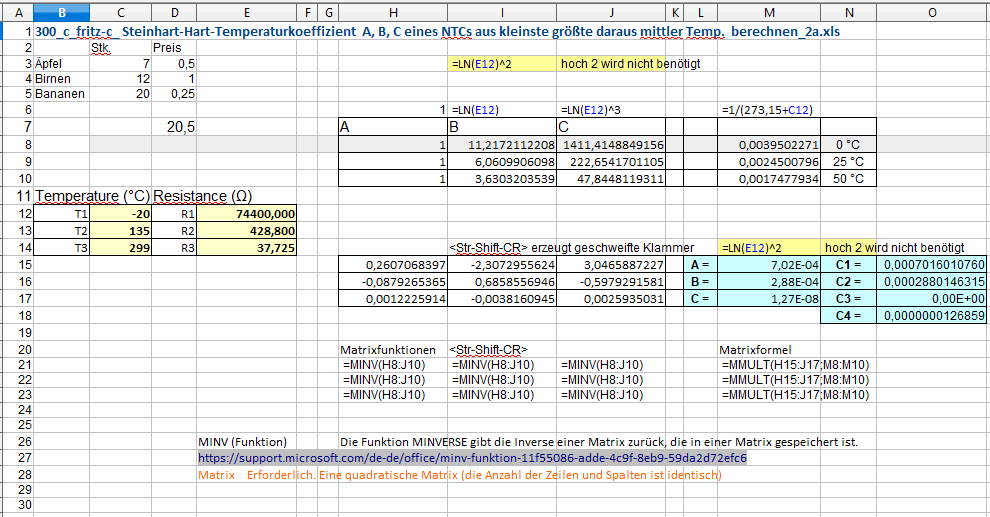







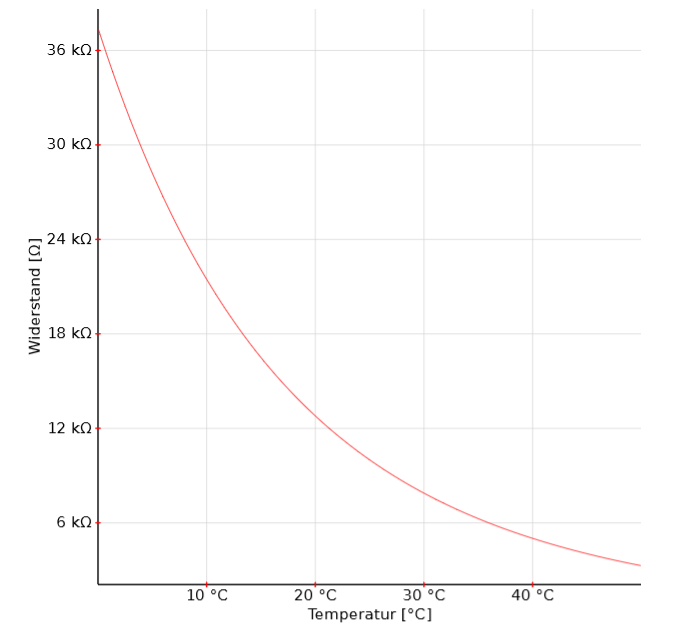
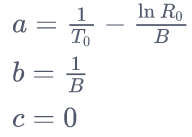


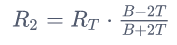



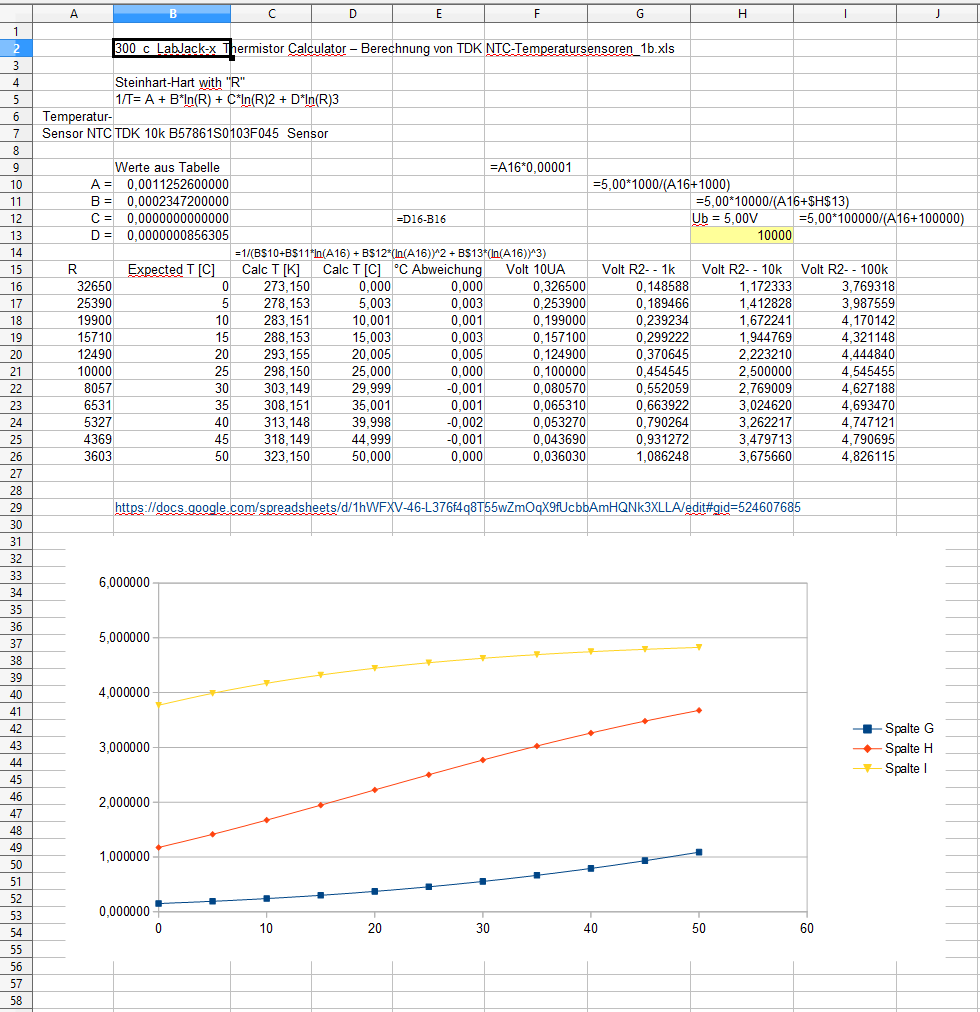






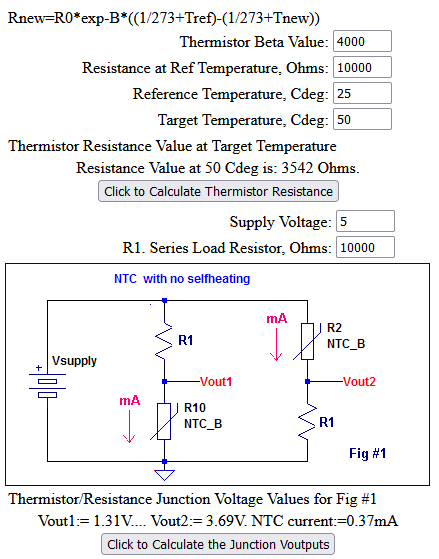

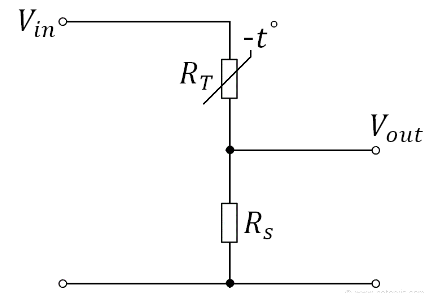







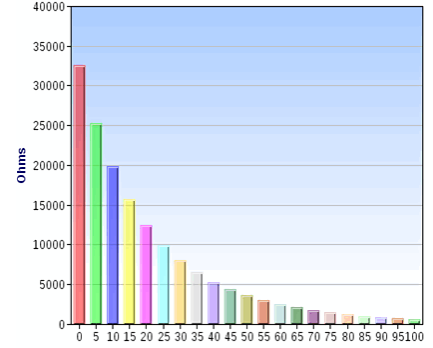




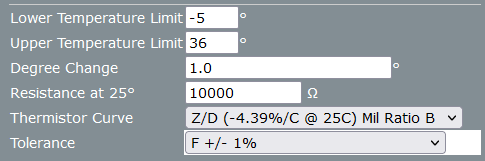








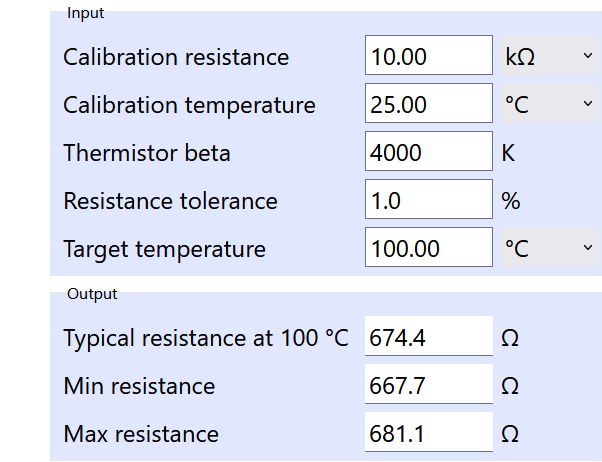


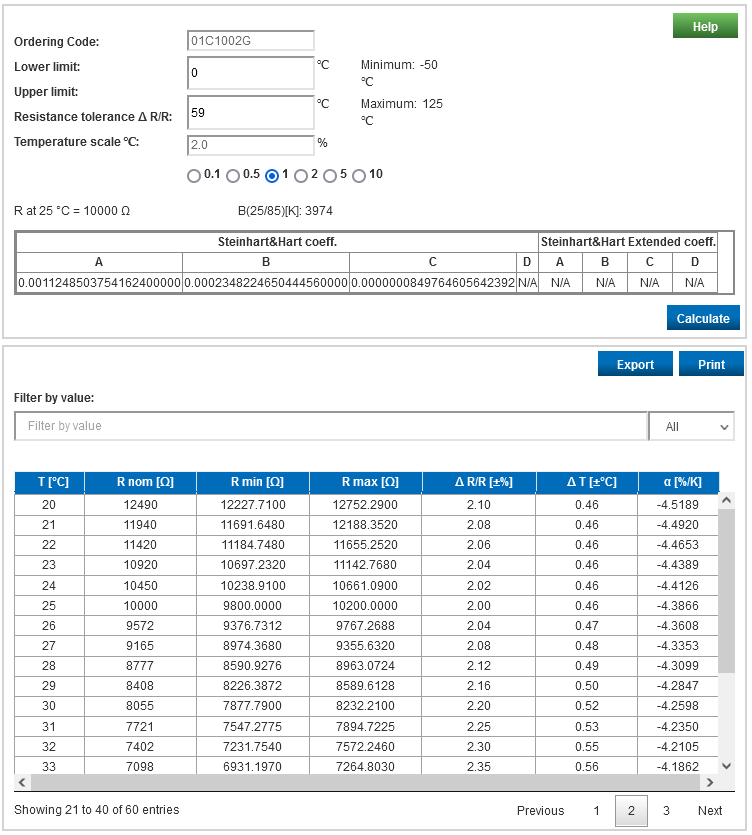





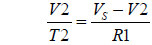
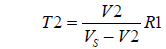

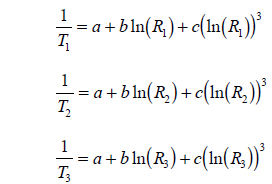
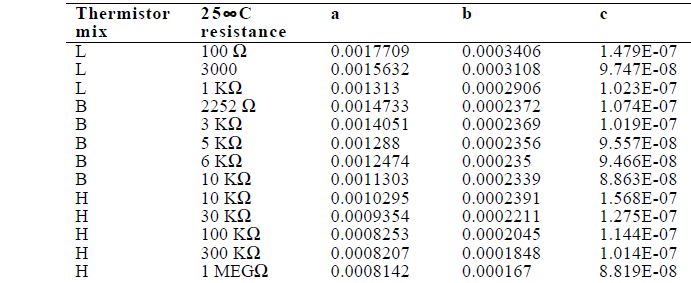

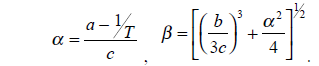


















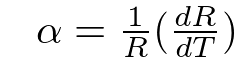





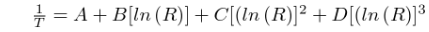





.png)