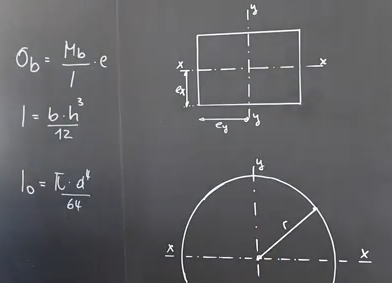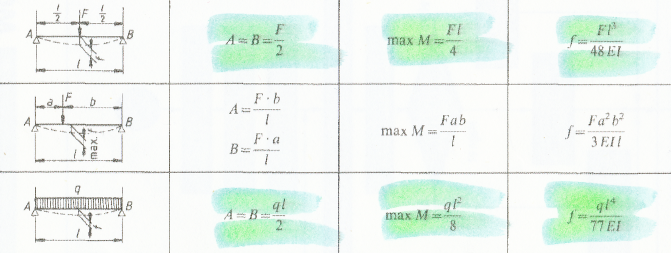http://sites.schaltungen.at/haus/holz/statikberechnung
http://www.linksammlung.info/
http://www.schaltungen.at/
Wels, am 2003-11-25
BITTE nützen Sie doch rechts OBEN das Suchfeld
[ ] [ Diese Site durchsuchen]
DIN A3 oder DIN A4 quer ausdrucken
*******************************************************************************I**
DIN A4 ausdrucken siehe
http://sites.schaltungen.at/drucker/sites-prenninger
********************************************************I*
~015_b_PrennIng-a_haus-holz-statikberechnung (xx Seiten)_1a.pdf
Untergeordnete Seiten (2):
siehe auch
http://sites.schaltungen.at/holz/statik
300_b_fritz-x_Excel Statikberechnungen_2b.xls
Passendes Holz für Ihr persönliches Bauprojekt
Leimbinder und Konstruktionsvollholz
Quelle:
https://holz-shop.com/Leimbinder-und-Konstruktionsvollholz--5129.html
Holzbau- Berechnunug und Konstruktion
(Auszug aus ÖNORM B4100-2, ,Holzbau Holztragwerke, Teil 2 : Berechnunung und Auslührung")
Tabelle1:
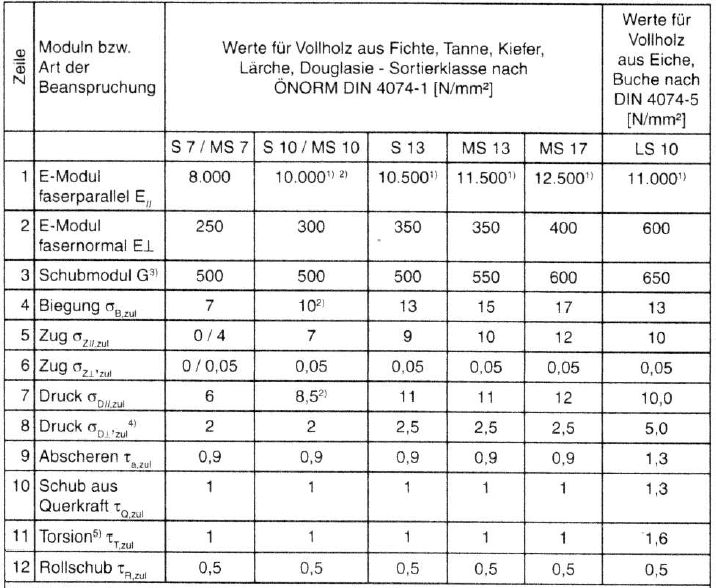
Elastizitätsmodul, Schubmodul und zulässige Spannungen für Vollholz , auch keilgezinkt (Holzfeuchte < 20 % der Darrmasse)
(nach ÖNORM B4100-2)
E-Modul E = 10.000 N/mm2
Schubmodul G = 500 N/mm2
Biegespannung zulässig σb = 10 N/mm2
Schun aus Querkraft tau = 1 N/mm2
1) Für Holz das mit einer Holzfeuchte von < 15% eingebaut wird, darf dieser Wert um 10% erhöht werden wenn beim Einbau die Holzfeuchle nachgewiesen wird.
2) Dieser Wert darf bei Baurundholz ohne Schwächung der Randzone um 20 % erhöht werden.
3) Der zur Rollschubbeanspruchung genhgörende Schubmodul dalrf mit GR= 0,10 G angenommen werden.
4) Wenng größere Eindrückungen unbedenklich sind und erforderlichefalls konstruktiv berücksichtig werden dürfen diese Werte um 20 % erhöht werden
(nicht bei Anschüssen mit verschieden Verbindungsmittel).
5) Für Kastenquerschnitte sind die Werten nach Zeile 10 einzuhallen.
Quelle:
300_c_fritz-x_Baustatik zulässige Spannungen Vollholz_1a.pdf
Bemessungstabellen Konstruktionsvollholz (KVH)
Bemessungsgrundlagen:
Die aufgeführten Bemessungstabellen dienen lediglich der Vorbemessung von KVH- Trägern.
Sie ersetzen nicht den statischen Nachweis!
Randbedingungen:
• Gleiche Feldweiten bei gleichmäßiger Lastverteilung / keine feldweise Betrachtung
• Das Eigengewicht der Träger ist nicht berücksichtigt !
• Holzart Fichte gem. DIN4074
• E-Modul : E= 10.000 N/mm²
• Zul. Biegespannung : σb = 10 N/mm²
• zulässige Durchbiegung f = l/300 ( fmax = 3,333 mm/m)
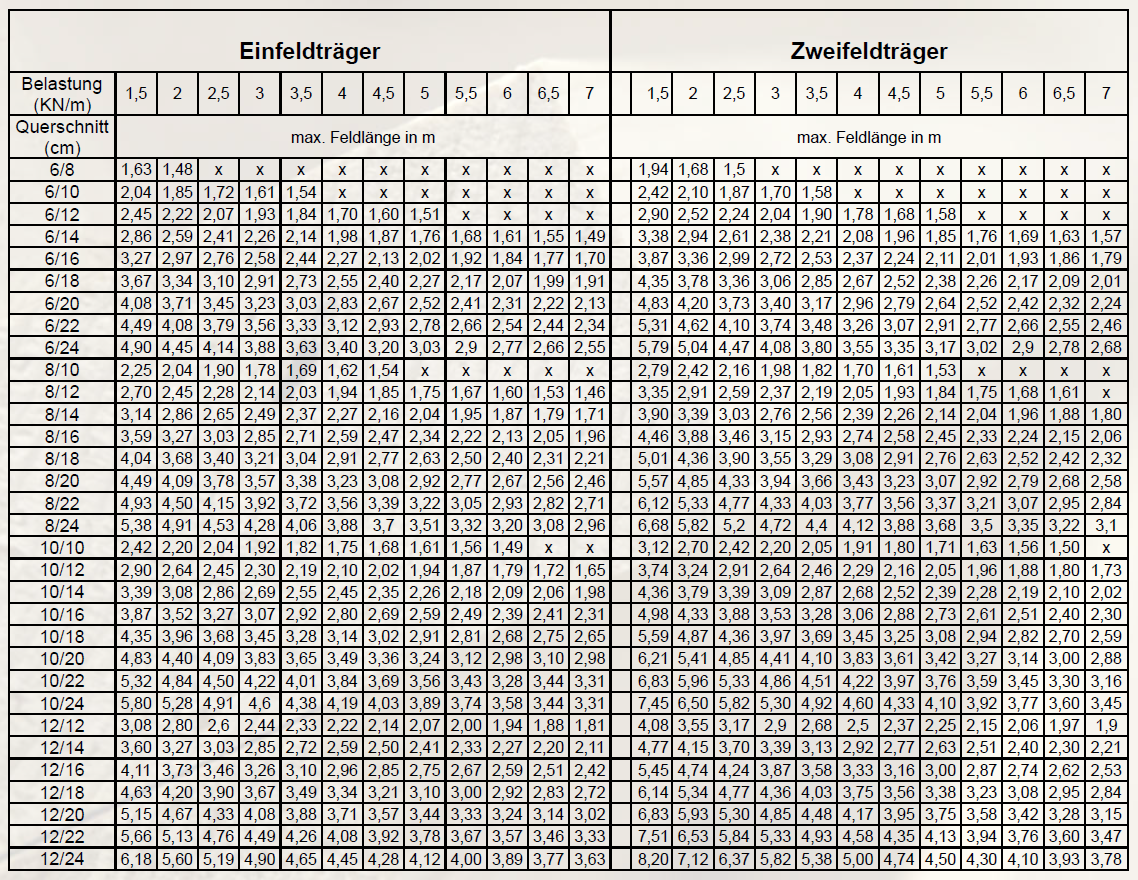
Linienlast
KVH 6/12 Belastung 1,5kN/m 2,45 (2,9m bei Zweifeldträger)
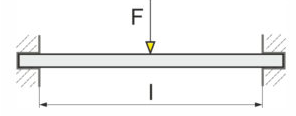
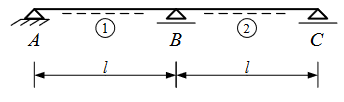
Zweifeldträger
Lasten
F n {\displaystyle F_{n}} 
|
äußere Kräfte F 1 {\displaystyle F_{1}}  , F 2 {\displaystyle F_{2}} , F 2 {\displaystyle F_{2}}  usw. usw.
|
M n {\displaystyle M_{n}} 
|
äußere Momente M 1 {\displaystyle M_{1}}  , M 2 {\displaystyle M_{2}} , M 2 {\displaystyle M_{2}}  usw. usw.
|
q {\displaystyle q} 
|
Streckenlast
|
Innere Kräfte (Schnittgrößen)
N x {\displaystyle N_{x}} 
|
Normalkraft im Balken
|
Q z {\displaystyle Q_{z}} 
|
Querkraft im Balken
|
M y {\displaystyle M_{y}} 
|
Moment im Balken
|
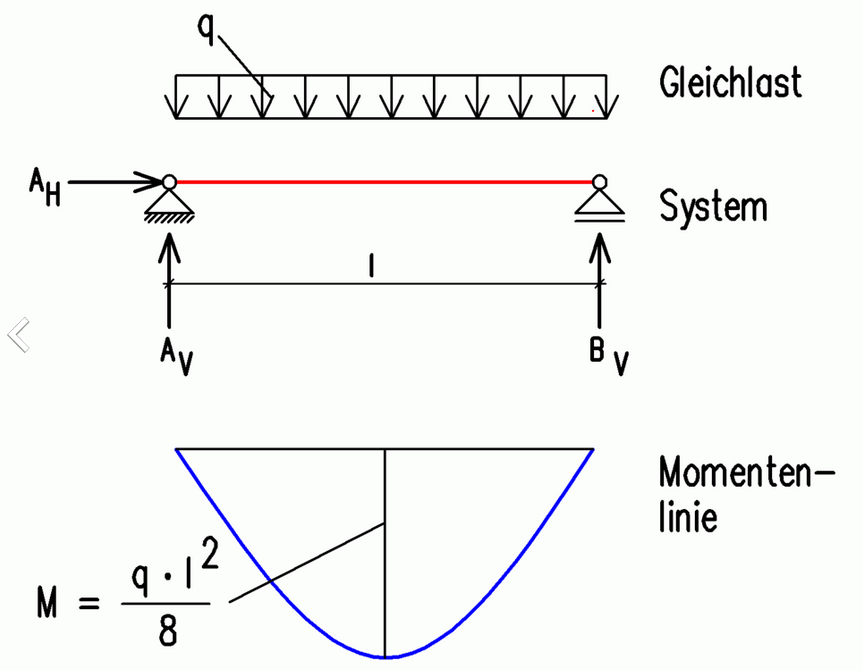
Maximales Biegemoment bei Gleichlast
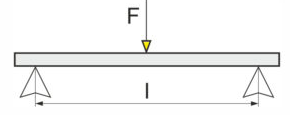
Als maximales Biegemoment eines Einfeldträgers mit Gleichlast ergibt sich:
-
M m a x = q ⋅ l 2 8 {\displaystyle M_{\mathrm {max} }={\frac {q\cdot l^{2}}{8}}}

Einfeldträger
Quelle:
https://de.wikipedia.org/wiki/Einfeldträger
300_c_fritz-x_Baustatik Bemessungstabellen Konstruktionsvollholz (KVH)_1a.pdf
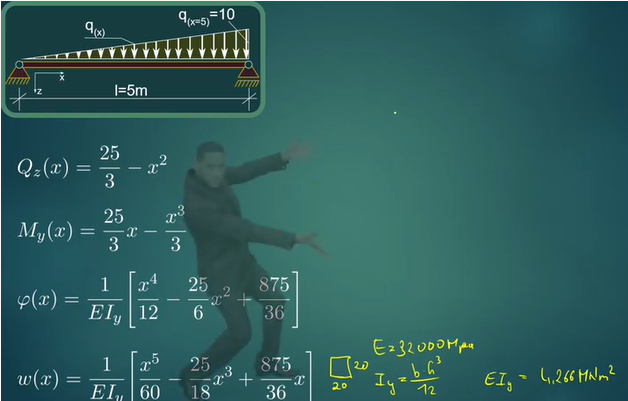
Statik Kraftgrößenverfahren Zweifeldträger Linienlast
Quelle:
https://www.youtube.com/watch?v=CmYHiitfqWg
https://bau.de/elearning/kraftgroessenverfahren/verfahren/beispiele/zwei-feld/print.php
https://www.bau.uni-siegen.de/subdomains/baustatik/lehre/bachelor/bst1/hoersaaluebung/bs1_hoersaaluebung_4_loesung.pdf
https://www.massivholzsystem.at/wp-content/uploads/2019/02/Statik-zweifeldtraeger.pdf
Balkenrechner für Biegemoment, Biegespannung, Querkraft & Auflagerreaktionen eines Trägers
https://www.johannes-strommer.com/rechner/balkenberechnung/
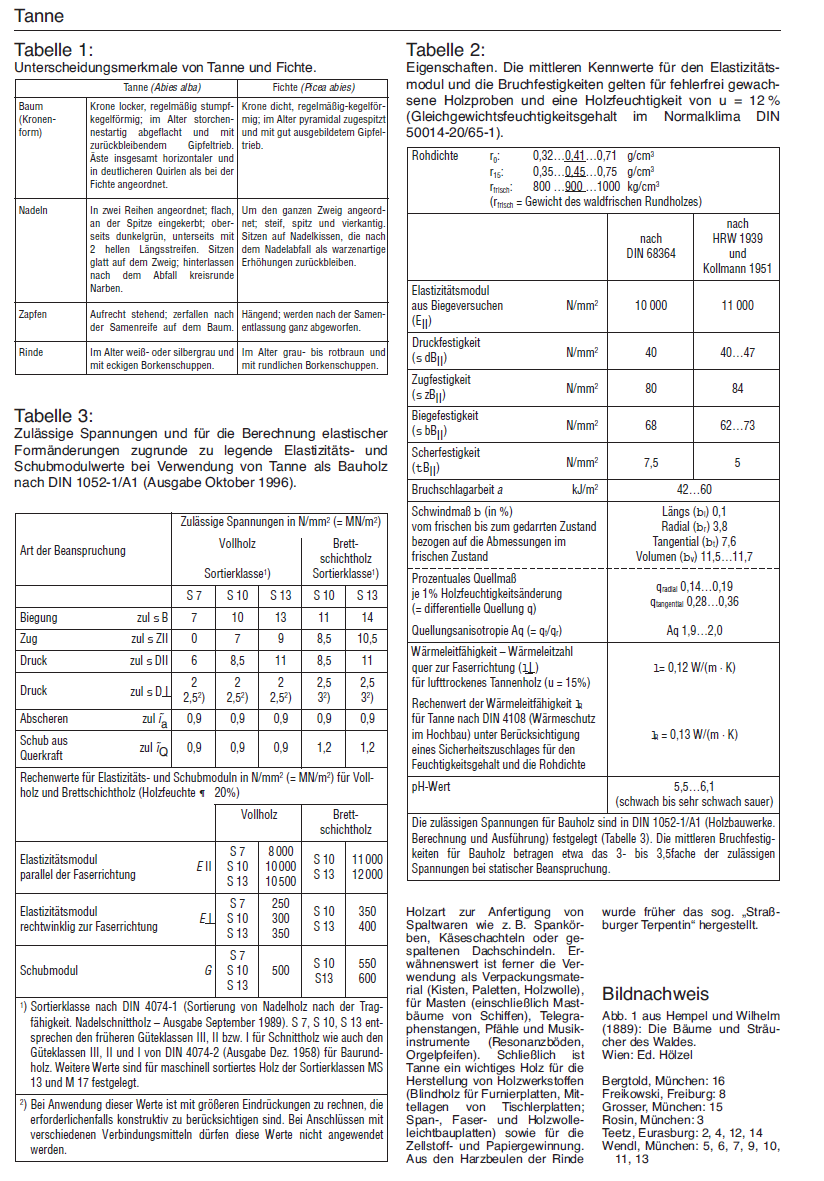
Elastizitäts- und Schubmodulwerte bei Verwendung von Tanne als Bauholz
nach DIN 1052-1/A1 (Ausgabe Oktober 1996).
Quelle:
300_c_fritz-x_Baustatik Elastizitäts- und Schubmodulwerte bei Verwendung von Tanne als Bauholz_1a.pdf
Keilgezinktes Vollholz nach DIN EN 15497:2014
Berechnungsbeispiel Holzbalkendecke
usw.
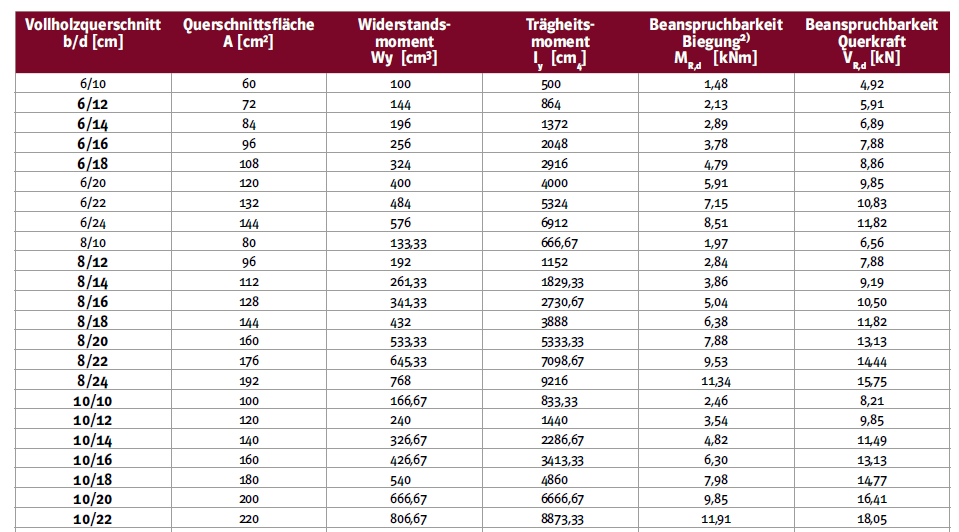
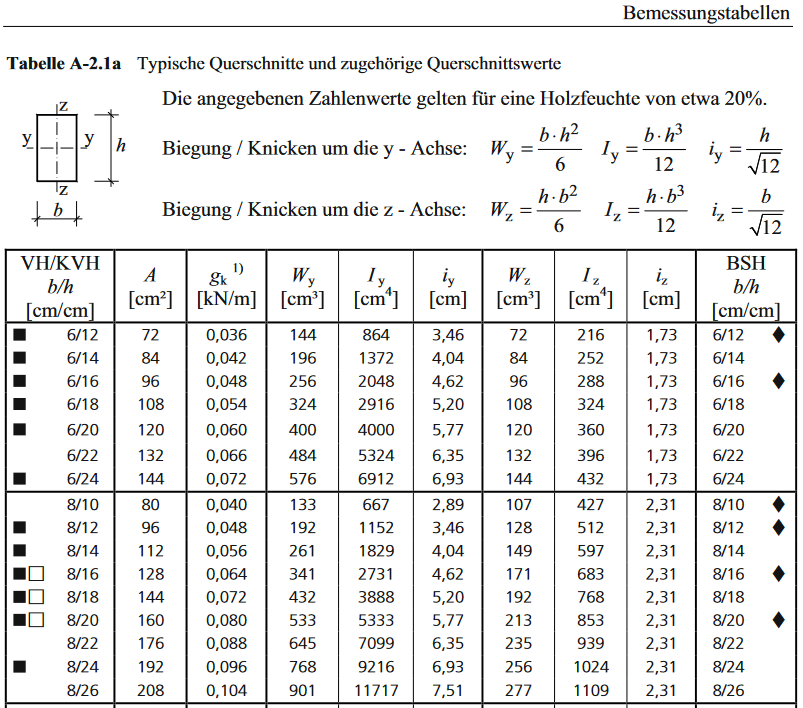
6.2 Querschnittswerte und Bemessungswerte
Tabelle 6.2 - Querschnittswerte und Bemessungswerte der Beanspruchbarkeit für Vorzugsquerschnitte der
Festigkeitsklasse C24 (Sortierklasse S10) 1) für NKL 1 und 2 bei KLED mittel
1) Bemessungswerte ermittelt für mittlere Lasteinwirkungsdauer in Nutzungsklasse 1 und 2: Modifikationsfaktor: kmod = 0,8; Teilsicherheitsbeiwert Vollholz: γM = 1,3
2) Beanspruchbarkeit Biegung M kNm um die starke Achse (y-y)
Quelle:
300_c_fritz-x_Baustatik KVH Konstruktionsvollholz - Technische Informationen_1a.pdf
********************************************************I*
Baustatik
Formelsammlung Statik
Quelle:
https://www.studydrive.net/de/tag/baustatik
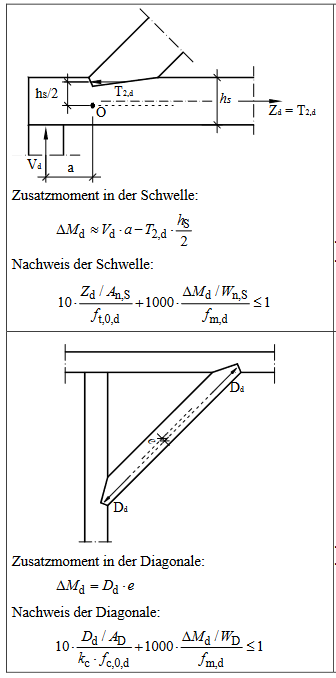
300_c_fritz-x_Baustatik Formelsammlung - Ausklinkungen und Verbindungen im Dachstuhlbau_1a.pdf
300_c_fritz-x_Baustatik FORMELN - Träger mit Linienlast_1a.pdf
300_c_fritz-x_Baustatik FORMELN - Träger auf zwei Stützen - Gleichlast_1a.pdf
BOOK
Rill, Georg
2019/06/01
ISBN: 978-3-527-71521-3
Technische Mechanik I Statik für Dummies
Statik für Maschinenbauer für Dummies
ISBN: 3527707611
Herausgeber : Wiley-VCH
357 Seiten
Formelsammlungen
Sammlungen mit naturwissenschaftlichen und mathematischen Formeln.
Quelle:
https://www.internetchemie.info/chemie/formelsammlungen.php
BUCH:
Alfred Böge
Formeln und Tabellen zur Technischen Mechanik
VIEWEG-Verlag
ISBN: 3-8348-1445-6
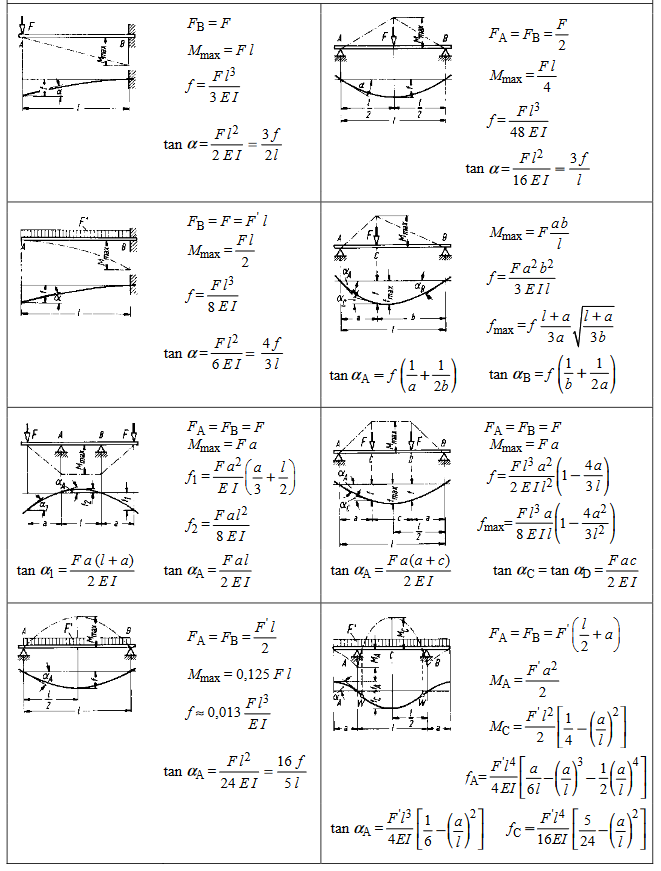
4 Festigkeitslehre
4.12 Stützkräfte, Biegemomente und Durchbiegungen bei Biegeträgern von
gleichbleibendem Querschnitt
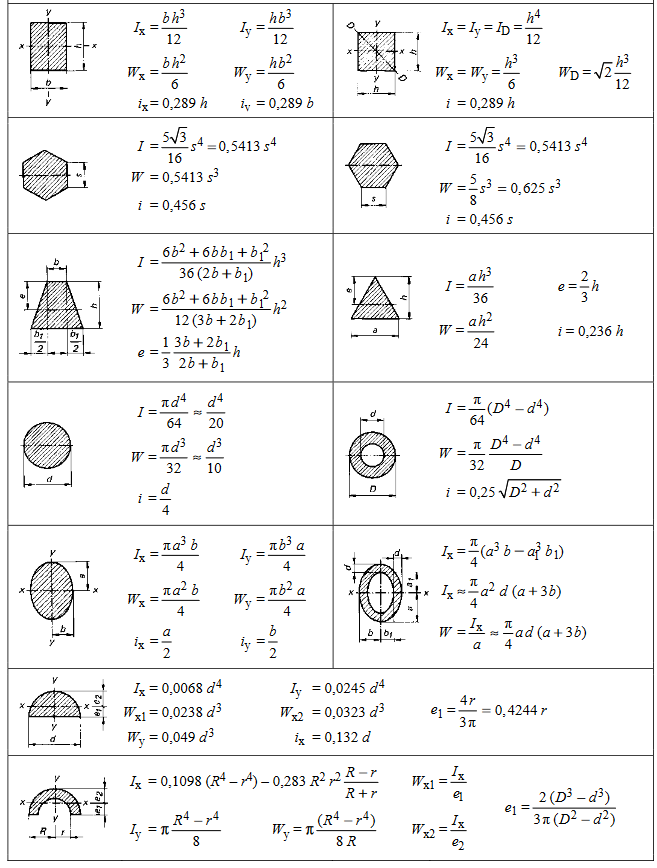
4.13 Axiale Flächenmomente 2. Grades I, Widerstandsmomente W und
Trägheitsradius i für Biegung und Knickung
300_c_Formeln-x_Formeln und Tabellen zur Technischen Mechanik_1a.pdf
300_c_Formeln-x_Formeln Baustatik_1a.pdf
Statik
Quelle:
http://technische-mechanik-feldmann.de/Statik.htm#ExtremalprinzipederMechanik
http://technische-mechanik-feldmann.de/Statik.htm#statikaufgeben
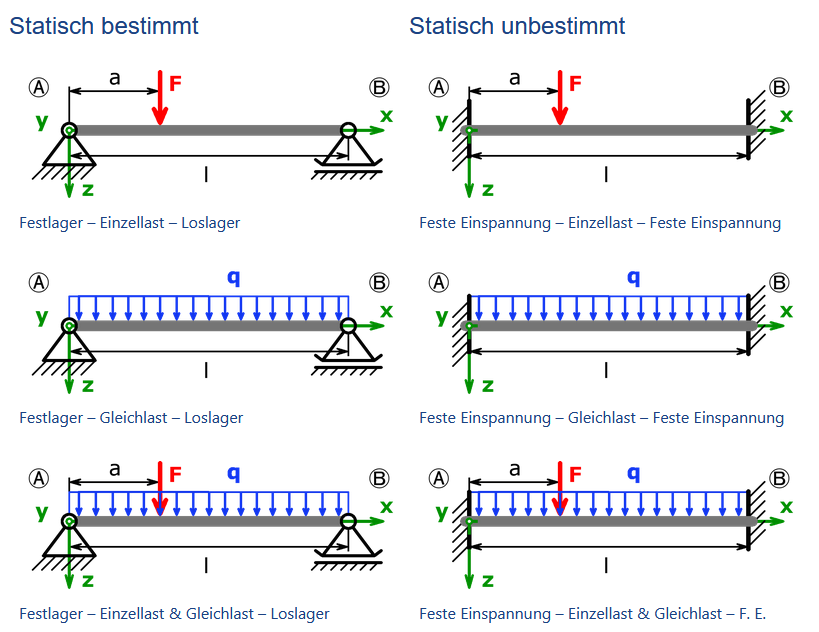
http://technische-mechanik-feldmann.de/Statik.htm#statischbestimmt
http://technische-mechanik-feldmann.de/Statik.htm
********************************************************I*
Berechnung des Brettschichtholz (BSH) Balken
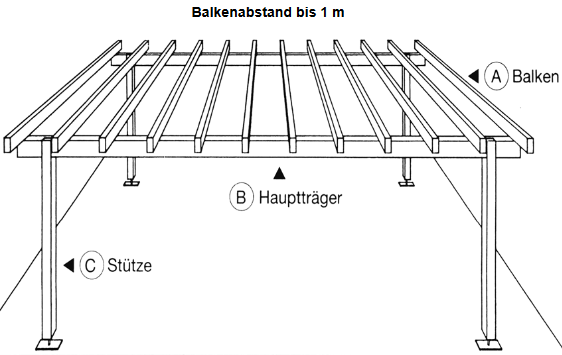
Draufsicht auf die Anordnung der Holzbalken an der Decke
Pfetten darauf Sparren
Stützen
Durchlaufträger
Baurechner Online — Kalk.Pro
max. Durchbiegung L/350 bei Estrich 1/350 = 2,85 mm/m
max. Durchbiegung L/300 bei Nadelholz 1/300 = 3,33 mm/m
max. Durchbiegung L/250 bei Holz 1/250 = 4,00 mm/m
max. Durchbiegung L/200 bei BSH 1/200 = 5,00 mm/m
https://de.wikipedia.org/wiki/Durchbiegung
Balken / Sparren aus
KVH = Konstruktionsvollholz L/300
BSH = Brettschichtholz L/200
MPX = Multiplexplatten (Sperrholz) L/200
RUN = Rundholz zweiseitig beschnitten L/300
Berechnung der Durchbiegung des Balkens (Biege -)
Biegemoment (Formel):
Mmax = q × l^2 / 8
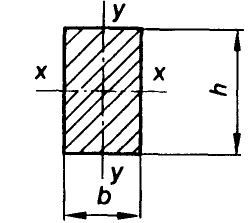
Widerstandsmoment des Balkens (Formel):
W = b × h^2 / 6
Bei Gleichlast über die Fläche
Die Durchbiegung des Balkens (Formel):
f = (5 × q × l^4 ) / (384 × E × Jx)
Trägheitsmoment (Formel):
Jx = b × h^3 /12
Die Durchbiegung des Balkens (die Formel):
f = (5 × q × l^4 ) / (384 × E × (b × h^3 / 12))
Berechnung des Brettschichtholz (BSH) Balken
b – Breite des Balkens;
h – die Höhe des Balkens.
A - Querschnittfläche des Profils
q – die Größe der Belastung auf die Überdeckung;
l – Größe des Bogens der Überdeckung.
Wx = Widerstandsmoment
Mmax – Wert der maximalen Biegemoment;
R – Wert der berechneten Widerstand des Holzes.
q – die Größe der Belastung auf die Überdeckung;
l – Länge (Größe des Bogens der überlappung)
E – Elastizitätsmodul Holz 10..15GPa
https://de.wikipedia.org/wiki/Elastizitätsmodul#Typische_Zahlenwerte
E-Modul von Holz E = 100000 kg/cm2 = 1000000 N/cm2 = 10000 N/mm2 = 10 GPa = 10.000 MPa = 1,45 Mpsi
https://www.precifast.de/elastizitaetsmodul-e-modul/
J – Trägheitsmoment.
fm - Durchbiegung des Balkens max.
sigma - Biegespannung Biegung σzul=
Fa = Auflagerkraft im Lager A
Fb = Auflagerkraft im Lager B
Gleichlast / Flächenlast
Trägheitsmoment (Formel) : J = b × h^3 /12
Widerstandsmoment des Balkens (Formel) : Wx = b × h^2 / 6
Biegemoment (Formel) : Mmax = q × l^2 / 8
Widerstandsmoment (Formel) : Wreq = Mmax / R
max. Durchbiegung des Balkens (Formel) : fmax = (5 × q × l^4 ) / (384 × E × I)
Quelle:
https://kalk.pro/de/
https://kalk.pro/de/holzbalken/
https://kalk.pro/de/holzbalken/brettschichtholz-bsh-balken/
https://kalk.pro/de/holzbalken/#raschet-balki-na-progib-izgib
https://kalk.pro/de/holzbalken/#maksimalnyj-izgibayushchij-moment
********************************************************I*
Terrassendach Carportdach Berechnung
Hier können Sie ablesen, welche HOLZ-Querschnitte Sie benötigen
Quelle:
https://lowis.de/assets/files/BSH-Berechnung.pdf
********************************************************I*
HoB.Ex
Bemessungshilfen auf EXCEL-Basis
Die Bemessung nach neuer DIN1052 ist im Vergleich zur „alten“ Holzbau-Norm deutlich rechenintensiver geworden.
Die Möglichkeiten, die die neue DIN 1052 eröffnet, können realistisch betrachtet nur unter Einsatz von EDV-Programmen genutzt werden.
Demoversion
Eine kostenlose Demoversion des HoB.Ex-Programms kann über
www.bauenmitholz.de/hob-ex.html
heruntergeladen werden.
300_c_fritz-x_HoB.Ex Bemessungshilfen auf EXCEL-Basis - Bookmatter Holzbau (52 Seiten)_1a.pdf
Quelle:
https://link.springer.com/content/pdf/bbm%3A978-3-8348-9551-6%2F1
********************************************************I*
Kostenpflichtig
Software Dimensionierungen von Stabtragwerken und Metallbaubauteilen.
Einfache statische Vorbemessung von Stabtragwerken und Metallbauteilen.
BALUSTAT ermöglicht schnelle und einfache Dimensionierungen von Stabtragwerken, Metallbaubauteilen und Verbindungen. Lastannahmen für Schnee und Wind können einfach ermittelt werden.
Quelle:
https://balustat.eu/?gclid=CjwKCAjwu_mSBhAYEiwA5BBmf0N_cvUhwvbnzca8iCPtCOIagY1g2OnEMMwJufBBlY3WKezGbVMSWxoCN-gQAvD_BwE
********************************************************I*
Max. Tragfähigkeit von Holzbalken
Reguläre Dachbalken (bei Verwendung eines Flachdaches)
Für die Dachbalken eines Holzdaches empfehlen wir Ihnen folgende Faustregel zu verwenden:
Pro 1m Überdachung sollte eine Holzstärke von 4..5cm verwendet werden.
Bei den Dachbalken betrachten wir jeweils nur den Abstand von Stützbalken zu Stützbalken, entsprechend sollte dies bei der Planung beachtet werden.
Angenommen, Sie möchten eine Überdachung mit der Breite von 3 Metern errichten, dann benötigen Sie Balken mit einer Stärke von 12..15 cm.
Für eine Breite von 4 Metern benötigen Sie Balken mit einer Stärke von 16..20 cm.
Es ist auch möglich, eine Überdachung von 5 Metern mit 20..25 cm starken Balken zu überdachen,
wobei durch den Einbau von stabilen Streben die Breite der Träger auf 6 Meter erhöht werden kann.
Bei leichten Dächern sollte diese Methode langfristig keine Probleme hervorrufen, jedoch empfehlen wir dies generell nicht, da dies durchaus langfristig dazu führen kann, dass Ihr Dach leicht durchhängt.
Quelle:
https://gadero.de/blog_maximale-tragfahigkeit-von-holzbalken/
********************************************************I*
Statikberechnung für Holzkonstruktionen
Berechnen einer 4 x 6m Holzterrasse Haidestr. 11A
Trägerabstand von 68 cm.
Max. Belastung pro Quadratmeter legen wir mit 150kg an
6×12 cm Träger
Quelle:
https://www.losmuchachos.at/allgemein/statik-fur-holz/
https://www.losmuchachos.at/holzbau/statik-fur-holztrager/
********************************************************I*
Formelsammlung für die Dachstuhlberechnung
Durchbiegung fmax = 5 / 384 * (q * l^3) / ( E * Jx) = 5/384 * (378,5kg * 350^3) / (100000 * 864) = 2,44cm
Quelle:
http://www.hs-augsburg.de/~colling/holzbau-colling/pdf/holzbau/Formelsammlung.pdf
********************************************************I*
VIDEOs
Prof. Dr. Eugen Nachtigall
Ingenieurbüro Nachtigal
Professor, Dr.-Ing., Bauingenieur, Dipl.-Wirt. Ing., Wirtschaftsingenieur
Michelsbergstr. 1
D-53913 Swisttal
Tel. +49 (0)151 156 / 66673
Tel. +49 (0) 2255 8586
Tel. +49 (0) 151 156 666 73
Lernplan Technische Mechanik 2 – Elastostatik
https://ingenieur.schule/
https://ingenieur.schule/technische-mechanik-2/
Lernplan Technische Mechanik 1 – Stereostatik
https://ingenieur.schule/technische-mechanik-1/
Quizze und Formelsammlungen zur Technischen Mechanik 1 und 2
https://ingenieur.schule/kurse/
Lernplan Technische Mechanik 3 – Dynamik
https://ingenieur.schule/technische-mechanik-3-dynamik/
Balkenbeigung Teil 1 – Vorlesung und Übung – Technische Mechanik 2
https://www.youtube.com/watch?v=NCe8q5hl01c
Balkenbiegung – Technische Mechanik 2
https://www.youtube.com/watch?v=OUKZhmM7c2M
Auflagerreaktionen und Schnittgrößen eines Einfeldträgers – Technische Mechanik 1
https://www.youtube.com/watch?v=K17v0r23tHY
Prof. Eugen Nachtigall
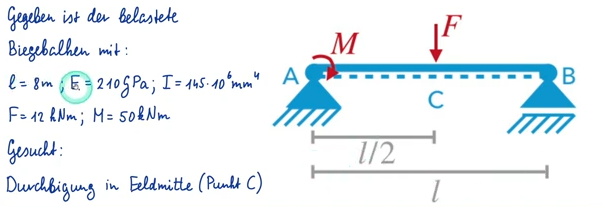
Durchbiegung berechnen mithilfe von Tabellen, Aufgabe – Technische Mechanik 2
F in Feldmitte
Quelle:
https://www.youtube.com/watch?v=LJ-HACs6Ppo
Dr. Eugen Nachtigall
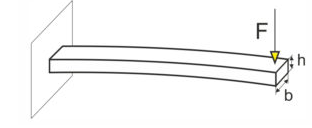
Biegebalken, Berechnung der Durchbiegung an einem Kragarmträger – Technische Mechanik 2
Quelle:
https://www.youtube.com/watch?v=bEj9ZbSg6xM
https://www.youtube.com/watch?v=bEj9ZbSg6xM
Prof. Dr. Eugen Nachtigall
Stabkräfte und Stabdehnungen bestimmen, Aufgabe – Technische Mechanik 2
https://www.youtube.com/watch?v=jrFUJSFItB4
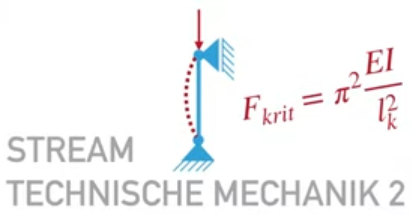
Knicken – Technische Mechanik 2
Quelle:
https://www.youtube.com/watch?v=uEbf0y0HgKA
Spannung und E Modul – Technische Mechanik 2 – Elastostatik
Quelle:
https://www.youtube.com/watch?v=5we_wPUt7RM
Spannung und Längenänderung – Technische Mechanik 2 – Elastostatik
Quelle:
https://www.youtube.com/watch?v=wRdaIz1F7UY
Windlast – Technische Mechanik 1 – Stereostatik
Quelle:
https://www.youtube.com/watch?v=LNOepObAlXg
Biegelinie
Stützträger mit Einzellast (5/5) Durchbiegung berechnen
Quelle:
https://www.youtube.com/watch?v=Ix4x0SwoI9M
Durchbiegung Einfeldträger - Arbeitssatz - Tabellenverfahren - Schnittgrößen - Statik
Quelle:
https://www.youtube.com/watch?v=qDq5H872Xpk
https://www.youtube.com/watch?v=qDq5H872Xpk
Festigkeitslehre
Biegespannung, passenden Querschnitt berechnen
https://www.youtube.com/watch?v=y76V01Rz5iA
Biegelinie eines Balkens bestimmen - Reine Biegung [Technische Mechanik] |StudyHelp
https://www.youtube.com/watch?v=aGwn6gHMf4M
Die wichtigsten Formeln eines Bauingenieurs | Teil 1
https://www.youtube.com/watch?v=yJ0P9xXk30s
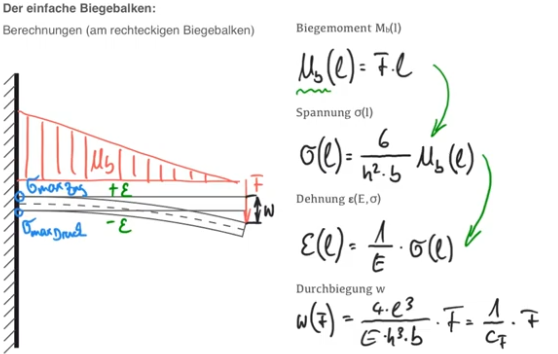
Der einfache Biegebalken
Quelle:
https://www.youtube.com/watch?v=Tr8kVecjRtI
Biegemoment | Widerstandsmoment | Biegespannung | Grundlagen | Biegung | Biegeträger
https://www.youtube.com/watch?v=k8uKTxGF8Ak
Was ist das Flächenmoment und Widerstandsmoment? | Einführung in die Spannungstheorie | Mechanik
https://www.youtube.com/watch?v=psIw_ABeIGs
Kopfbänder verschrauben beim Gartenhaus Bauen
Quelle:
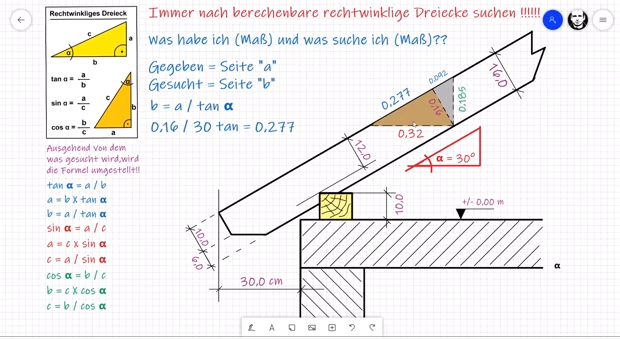
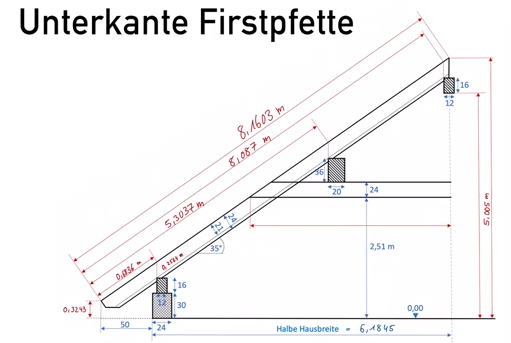
Rechnerischer Abbund für Zimmerer
https://youtu.be/W7NXwIqhO6w
Thema DACH #3 Rechnerischer Abbund (Sparrenprofil)
Quelle:
https://youtu.be/nKamNFDGwYI
Biegemoment | Widerstandsmoment | Biegespannung | Grundlagen | Biegung | Biegeträger
Quelle:
https://www.youtube.com/watch?v=k8uKTxGF8Ak
Kochrezept bei Aufgaben zum Biegebalken [Technische Mechanik] |StudyHelp
Quelle:
https://www.youtube.com/watch?v=4NaS4JJGYQk
Balkentheorie - Biegelinie eines Einfeldträgers unter einer Dreiecklast - DGL
Quelle:
https://www.youtube.com/watch?v=BvbsJDbhGPQ
Normalspannung / Biegespannung bestimmen [Technische Mechanik] |StudyHelp
Quelle:
https://www.youtube.com/watch?v=bboIGmganpY
********************************************************I*
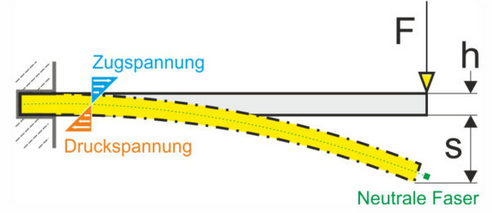
Biegespannung berechnen
Formel Biegespannung
Für die Berechnung der Biegespannung

[Nmm²] wird folgendes benötigt:
das Biegemoment „Mb“ [Nmm] und
das Widerstandsmoment „W“ [mm³].
l = Länge der Feder
F = Kraft
 = Mb / W
= Mb / W
Mb = F * l
Mb = F * l / 4
Berechnung Widerstandsmoment „W“
Das Widerstandsmoment „W“ [mm³] berücksichtigt den Widerstand gegen die Durchbiegung.
Aus diesem Grund wird es häufig als Biegewiderstandsmoment bezeichnet.
Für die Größe „Widerstandsmoment“ ist allein die Geometrie (Breite x Höhe in mm) der jeweils betrachteten Formfeder-Querschnittsfläche ausschlaggebend.
W = J / 
J = b*h^3 / 12
 = h / 2
= h / 2
Blattfeder Berechnung
Formeln:
Maximale Biegespannung

Maximale Federkraft

Federweg (Durchbiegung)

 für Rechteck-Blattfeder (Variante a)
für Rechteck-Blattfeder (Variante a)  = 4
= 4
 für Trapez-Blattfeder (Variante b)
für Trapez-Blattfeder (Variante b) ![q_{{1}} \approx 4 \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]](https://chart.apis.google.com/chart?cht=tx&chl=q_%7B%7B1%7D%7D%20%5Capprox%0A4%20%5Ccdot%20%0A%20%5Cleft%20%5B%203%2F%20%5Cleft%20(%202%2Bb2%2Fb%20%5Cright%20)%5Cright%20%5D)
Maximaler Federweg (Durchbiegung)

Maximale Federblattstärke

 für Rechteck-Blattfeder (Variante a)
für Rechteck-Blattfeder (Variante a)  = 2/3
= 2/3
 für Trapez-Blattfeder (Variante b)
für Trapez-Blattfeder (Variante b) ![q_{{2}} \approx \left ( 2/3 \right ) \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]](https://chart.apis.google.com/chart?cht=tx&chl=q_%7B%7B2%7D%7D%20%5Capprox%0A%5Cleft%20(%202%2F3%20%5Cright%20)%20%5Ccdot%20%0A%20%5Cleft%20%5B%203%2F%20%5Cleft%20(%202%2Bb2%2Fb%20%5Cright%20)%5Cright%20%5D)
Federrate

b = Breite Blattfeder (mm)
b2 = kleinere Breite Trapez-Blattfeder (mm)
E = Elastizitätsmodul
F = Federkraft (N)
h = Materialsträke Federblech / Federblatt (mm)
L = Länge Blattfeder (mm)
s = Federweg (mm)
Quelle:
https://info.formfedern.com/blattfeder-berechnung/
https://info.formfedern.com/biegespannung-berechnen/
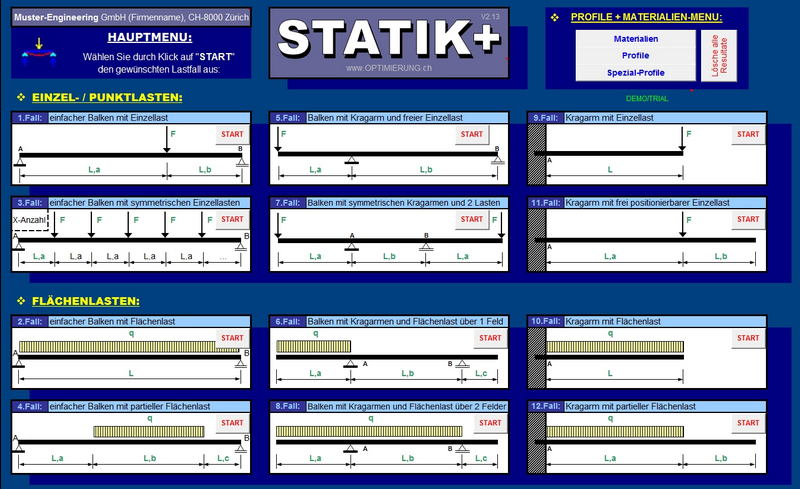
STATIK+ mit Excel
Mit diesem Excel-Programm dimensionieren Sie statisch bestimmte Tragwerke
30 Tage testen möglich
Quelle:
http://www.optimierung.ch/Beschrieb_Statik.shtml
********************************************************I*
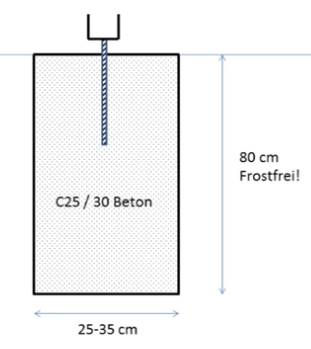
Carport Statik leicht gemacht (1A)
Stütze 14x14cm
Einfacher Standsicherheitsnachweis für einen Balken (Einfeldträger)
Sparrenabstand 80cm
Sparren 8 x20cm = 0,08m x 0,20m * 6m = 0,096m3 x 600kg/m3 = 57,9kg / 6 = 9,6kg/m
Dachhaut (Trapezblech) 13 kg/m2
1. Ermittlung Gewicht (ständige Lasten)
Trägerabstand 80 cm 13kg/m2 * 0,8 = 10,40 kg/m
Holzträger (600 kg/m3) 0,08 x 0,20m 9,60 kg/m
Summe: 20,00 kg/m = 200N/m = 0,2kN/m
2. Ermittlung Schneelast je nach Schneelastzone
Von 52 kg/m2 bis 700 kg/m2
bei Schneehöhe von 62,5 cm 125kg/m2 = 1250N/m2 = 1,25kN/m2
Für den Nachweis der Linien-Last
g = 20,00 kg/m = 200N/m = 0,200 kN/m (ständige Last)
q = 1,25 kN/m2 x 0,8 m = 1,000 kN/m ( Schneelast )
Summe der Last pro Meter = 1,200 kN/m
Einfacher Standsicherheitsnachweis für einen Balken (Einfeldträger)
System:
6m Sparren 8 x 20 cm
Nachweis der Biegung des Trägers: (Last pro m * Länge^2 / 8)
Berechnungen mit Sicherheitsfaktoren macht keinen Sinn man kann ja mit höheren Schneelasten rechnen!
My = 1,2 kN/m * 6m^2 / 8 = 5,4 kNm = 540 kNcm ( die max. Biegung)
Widerstandsmoment des Trägers 8/20 (b*h^2/6)
Wy= b * h^2 / 6 = 8 * 20^2 / 6= 533cm3
Nachweis:
M / Wy = 540 kNcm / 533 cm3 = 1,013 kN/cm2 (max. errechnete Spannung im Sparren)
Die max. Spannung für Nadelholz S10 C24 (Bauholz) im überdachten Bereich muß < 1,66 kN/cm2 sein!
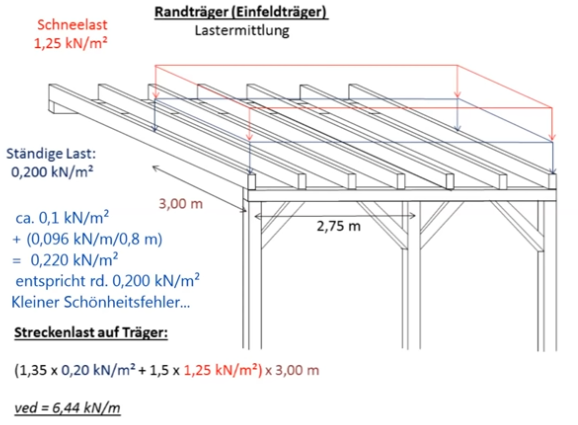
Nachweis für Randträger (Einfeldträger) Lastermittlung
Schneelast = 1,25 kN/m2
Standige Last: = 0,2 kN/m2
Streckenlast auf Träger: 0,20 kN/m2 + 1,25 kN/m2 x 3,00 m = 4,35 kN/m ved = 6,44 kN/m
Schneelast = 1,25 kN/m2
Ständige Last = 0,2 kN/m2
ca. 0,1 kN/m2 + (0,096 kN/m/0,8 m) = 0,220 kN/m2 entspricht rund 0,200 kN/m2 (kleiner Schönheitsfehler !)
Streckenlast auf Träger:
Streckenlast auf Träger: 0,20 kN/m2 + 1,25 kN/m2 x 3,00 m = 4,35 kN/m ved = 6,44 kN/m
Träger 14x16 cm
Nachweis der Biegung des Trägers: (Last pro m • Länge / 8)
Myd = 4,35kN/m x 2,75m^2 / 8 = 4,11 kNm = 411 kNcm 609kNcm
Widerstandsmoment des Trägers 14x16 cm
Wy = b * h^2 / 6) =14 x 16^2 / 6 = 597cm3
Nachweis:
My / Wy = 411 kNcm / 597 cm3 = 0,688 kN/cm2 < 1,29 kN/cm2 (max. Spannung für Nadelholz S10 C24 im Freien bei direkte Beregnung)
Quelle:
https://www.youtube.com/watch?v=B2ZZWP0VZ2U
********************************************************I*
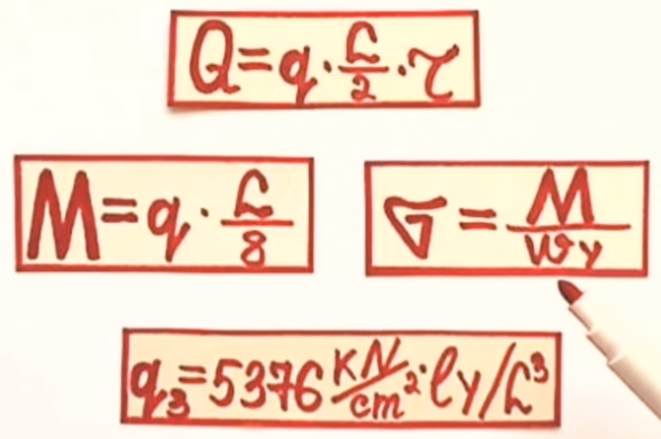
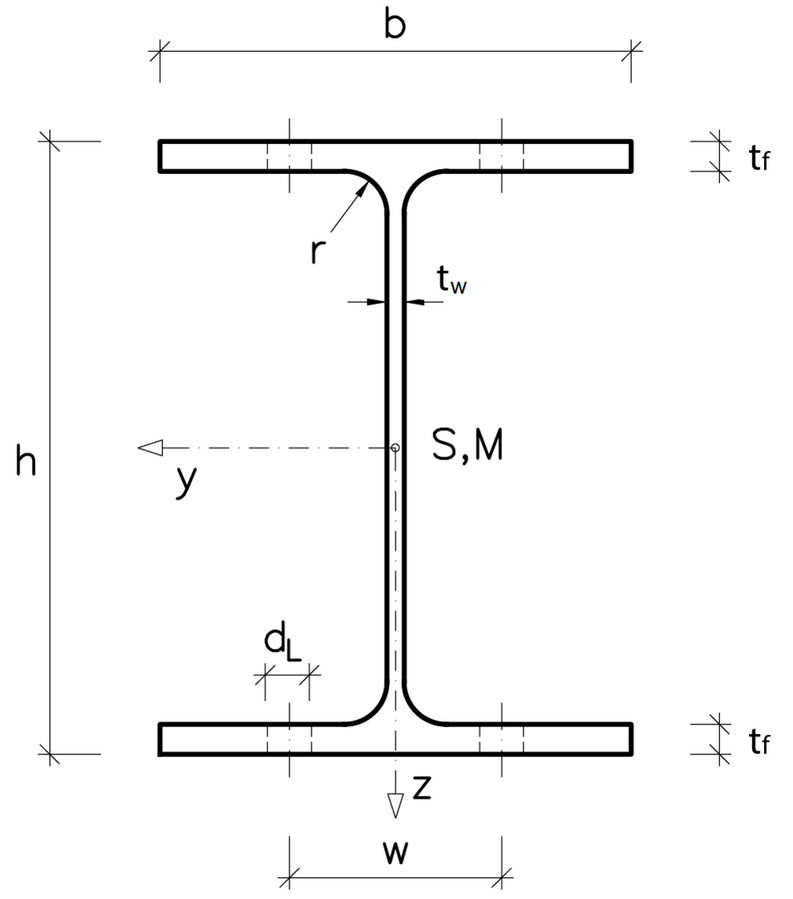
Statische Berechnungen eines Stahlträgers
HE-A Profil nach DIN1025-3
HEA - leichte Träger
L = Länge
q = Querkraft (Kraft = F auf den ganzen Stahlträger)
tau = Tau
M = Biegemoment
sigma = Biegespannung
Wy = Widerstandsmoment
q3 = Durchbiegung
Jx = Flächenträgheitsmoment
Biegemoment M = q * l / 8
q = M * 8 / l = 26133kpcm * 8 / 350cm = 597kg
q = (M * 8) / l = (16560 * 8) / 350 = 378,5kg
q = (8 * sigma b zul. * Wy ) / l = (8 * 115kg/cm2 * 144cm3) / 350 = 378,5kg
sigma b zul. = M / Wy = 16560kgcm / 144cm3 = 115kg/cm2
M = Wy * sigma b zul. = 144cm3 * 115kg/cm2 = 16560kgcm
https://www.youtube.com/watch?v=vPatZcPVmGs
HE 100A
h = 96mm
b = 100mm
tw = 5mm
tr = 8mm
A = 21,2 mm^2*10^2
Jy=349 mm^4*10^3
Wy = 72mm^3*10^3
https://bauforumstahl.de/wissen/stahlprofile
********************************************************I*
Download Top1 DE Entwurfs V4.13 - frei 1 Jahr funktioniert nicht mehr!
Holzkonstruktionen-Berechnungsprogramm TOP1
3 1/2" Diskette DIN1052 / 1055 Holzkonstruktionen deutsch TOP1 V4.13
top1e413.exe
Seriennummer : top1dee-06041
Startkode : DTKNEUA
(Dora Theodor Kaufmann Nordpol Emil Ulrich Anton)
Veenhoven Bouwinformatica
Quelle:
http://www.veenhoven.com/top1de_
********************************************************I*
FSTATIK
tfstatik.exe
Version:2.3
Sprachen:Deutsch
Lizenz:Shareware
Plattformen:Windows XP, Windows Vista, Windows 7, Windows 8, Windows 9x, Windows ME, Windows 2000
FSTATIK
ist das unverzichtbare Programm, um Berechnungen im Statikbereich schnell und fehlerfrei durchzuführen.
Darüber hinaus besitzt es eine leicht zu bedienende Benutzeroberfläche, mit deren Hilfe Träger-Kalkulationen erstellt und weitere Berechnungen aufgenommen werden können.
Ausgehend von 15 Grundprofilen lassen sich mit FSTATIK einfach Querschnittsflächen, Trägheitsradien oder -momente sowie Widerstandsmomente berechnen.
Dabei bietet das Berechnungsprogramm für Statik mehrere Zusatzmenüpunkte, mit denen an den analysierten Profilen die verschiedenen auftretenden Spannungen durch Zug, Druck, Torsion oder Biegung ermittelt werden.
Quelle:
https://www.giga.de/downloads/fstatik/
********************************************************I*
Güteklassen von Holz neu S alt GK
Die Holzqualität (Festigkeitsklasse) nach DIN1052, Teil 1, Tabelle 1 und 5.
Die Standard-Materialien umfassen folgende Klassen:
Brettschichtholz: Brettschichthölzer werden nach ihrer Festigkeit eingestuft in die Klassen BS 11, BS 14, BS 16 und BS 18,
die europäischen Bezeichnungen lauten GL 24, GL 28, GL 32 und GL 36.
Neue Festigkeitsklassen / EN 14080 (DIN 1052)
BS-Holz : BS11/GKII, BS14/GKI, BS16, BS18
Die früheren BS-Bezeichnungen sind wie folgt zu übertragen:
BS11 = GL24, BS14 = GL28, BS16 = GL32.
Quelle:
https://www.brettschichtholz.de/publish/0940a029_20ed_76a6_2c9a5dae9c0493e3.cfm
https://www.brettschichtholz.de/publish/1a291358_20ed_76a6_2ce35de9a58b0e0b.cfm
KERTO : Kerto-S, Kerto-Q
Nadelholz : S7/GKIII, S10/GKII, S13/GKI, MS13, MS17
Laubholz : A, B, C
Rundholz : S10/GKII, S13/GKI
'S' verweist auf die neue Klasseneinteilung nach DIN 1052 A1,
'M' auf maschinelle Sortierung.
Obwohl die Festigkeitswerte in Bezug auf die alten Werte geändert wurden, sind auch die Güteklassen (GK) angegeben.
********************************************************I*
Festigkeitsklassen - Brettschichtholz
Quelle:
https://www.brettschichtholz.de/publish/0940a029_20ed_76a6_2c9a5dae9c0493e3.cfm
https://www.holzhirsch.de/publish/binarydata/_relaunch_2017/sortiment/bauen_mit_holz/bsh/info_bsh-festigkeitsklassen_hirsch.pdf
https://de.wikipedia.org/wiki/Brettschichtholz
https://wissenwiki.de/Brettschichtholz
********************************************************I*
Broschüre "Holz richtig ausgeformt"
https://www.holz-fair-kaufen.at/wp-content/uploads/2020/06/Holz-richtig-ausgeformt.pdf
Güteklasse A Wertholz mangelfrei
Güteklasse B mittlere Qualität
Güteklasse C unterdurchchnittliche Qualität
Güteklasse Cx mindere Quallität nur für den Sägeverschnitt
Rundholzvermessung nach ÖHU 2006 (Österreichischen Holzhandelsusancen)
Quelle:
https://www.prehofer-holz.at/fileadmin/bilder/Holzinfo/Downloads/Holzlexikon.pdf
https://holzbrueckenbau.com/wp-content/uploads/R04_T02_F03_Konstruktive_Vollholzprodukte.pdf
********************************************************I*
Ideale Holzfeuchte
Frisch geschlagenes Holz enthält, abhängig von Holzart, Standort und Alter des Baums, bis zu 80 Prozent Feuchtigkeit – zu viel zum Bauen.
Ideales Bauholz ist nur so feucht wie die Luft in seiner zukünftigen Umgebung.
Fachleute sprechen von Gleichgewichtsfeuchte.
Diese Werte gelten nach der Norm DIN 1052:
• für allseitig geschlossene Bauwerke mit Heizung : 9 +/- 3 Prozent
• für allseitig geschlossene Bauwerke ohne Heizung : 12 +/- 3 Prozent
• für überdeckte offene Bauwerke : 15 +/- 3 Prozent
• für Konstruktionen, die der Witterung ausgesetzt sind : 18 +/- 3 Prozent
Quelle:
https://www.haus.de/bauen/holz-kaufen-qualitaet-erkennen-und-bauschaeden-verhindern-22206
********************************************************I*
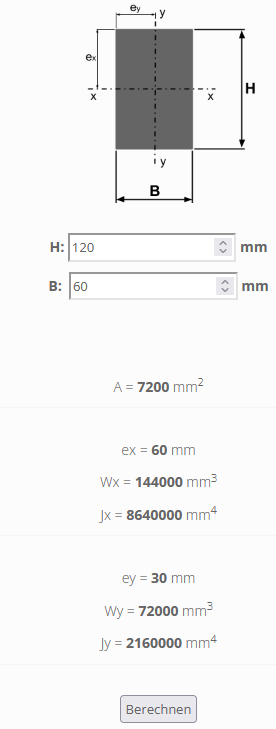
Online-Berechnung Widerstandsmoment Wx und Trägheitsmoment Jx
Rechteck Holz Sparren 6/12
Sparren 6x12 cm Fichte Leimbinder GL24 (BS11) SI nach DIN 1052
A = b * h = 6 * 12 cm = 72 cm2 (Fläche) 7200 mm2
Widerstandsmoment Wx = (b * h^2) / 6 = (6 *12^2) / 6 = 144 cm3 144.000 mm3
Trägheitsmoment Jx = (b * h^3) / 12 = (6 *12^3) / 12 = 864 cm4 8.640.000 mm4 ( = 8,64*10^6 mm4 )
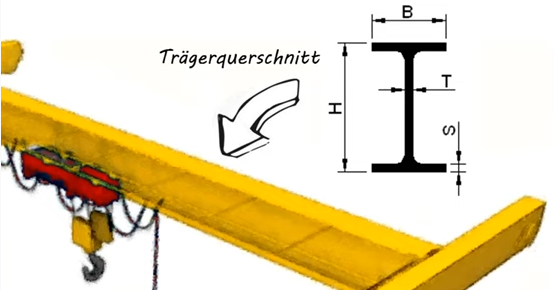
Definition Widerstandsmoment: Wx
Unter Widerstandsmoment W versteht man in der Festigkeitslehre eine nur aus der Geometrie eines Trägerquerschnittes (Form und Abmessung - nicht Material!) abgeleitete Größe.
Sie gibt an, welchen Widerstand der Träger bei Belastung den dabei entstehenden innereren Spannungen entgegensetzt.
Bei der Belastung durch Biegen spricht man vom axialen oder Biegewiderstandsmoment Wax, bei der Belastung durch Verdrehung (Torsion) vom polaren oder Torsionswiderstandsmoment Wp.
Die Berechnungen oben ermitteln das axiale Widerstandsmoment Wx / Wy.
Das Widerstandsmoment eines Trägerquerschnittes steht in Zusammenhang mit dem Flächenträgheitsmoment, mit dessen Hilfe bei statischen Berechnungen die Verformung eines Trägers unter Krafteinwirkung berechnet wird.
Bei Kräften senkrecht zu der jeweiligen Bezugsachse will die auftretende Kraft den Körper biegen bzw. um diese Achse drehen.
Wird die Drehung durch ein Festlager verhindert, entsteht ein Biegemoment.
Widerstandmomente werden immer in Bezug auf die jeweilige Momentenachse (x/y) berechnet.
Einheiten Widerstandsmoment (SI): m3, cm3, mm3.
Definition Flächenträgheitsmoment: Jx
Unter
Flächenträgheitsmoment J - oder auch als Flächenmoment 2. Grades bezeichnet - versteht man in der Festigkeitslehre eine aus dem Trägerquerschnitt abgeleitete geometrische Größe, die zu statischen Berechnungen bei Biege- und Torsions-Beanspruchung eingeführt wurde.
Unter dem Trägeheitsmoment einer Fläche versteht man einen Ausdruck, der dadurch gebildet wird, dass man die Fläche in Flächenteilchen zerlegt, jedes davon mit dem Quadrat seines Abstandes von der jeweiligen Bezugsachse multipliziert und aus diesen Produkten die Summe bildet.
Der Wert ist immer positiv, nie Null oder negativ.
Mit Hilfe des Flächenträgheitsmoments werden die Kräfte berechnet, die zur Dimensionierung eines Trägers benötigt werden.
Achtung:
Das Flächenträgheitsmoment nicht mit dem Massenträgheitsmoment verwechseln, das die Trägheit eines rotierenden Körpers gegenüber einer Winkelbeschleunigung beschreibt.
Die Berechnungen oben ermitteln das Flächenträgheitsmoment Jx / Jy.
Einheiten Flächenträgheitsmoment (SI): m4, cm4, mm4.
Quelle:
https://www.online-berechnung.at/widerstandsmoment-traegheitsmoment.html
********************************************************I*
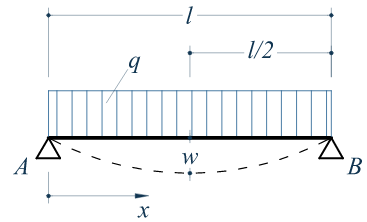
Maximales Biegemoment bei Gleichlast
Als maximales Biegemoment eines Einfeldträgers mit Gleichlast ergibt sich:
Formelsymbole
 Streckenlast
Streckenlast [kN/m]
 Stützweite
Stützweite des Trägers [m]
Quelle:
https://de.wikipedia.org/wiki/Einfeldtr%C3%A4ger#Maximales_Biegemoment_bei_Gleichlast
https://de.wikipedia.org/wiki/Träger_(Statik)
https://de.wikipedia.org/wiki/Statische_Berechnung
https://de.wikipedia.org/wiki/Balkentheorie
********************************************************I*
********************************************************I*
Statische Berechnung
Bemessungsprogramm für Holz-Konstruktionen
www.veenhofen.com
Garagendach Haidestraße 11A
DIN1052 Holzkonstruktionen v4.13 top1e413.exe
Dachstuhl - Zimmermann
Sparren - Binder - Träger - Pfetten
Holzqualität nach DIN1052 TL1 BS-Holz GL28 = BS14 = GK1 oder Nadelholz S10
Feuchteklasse 18%
Sparren Güteklasse II sigma zul. = 100kg/cm2 = 10000kg/m2
E-Modul von Holz E = 100000 kg/cm2 = 1000000 N/cm2 = 10000 N/mm2 = 10GPa = 1,45 Mpsi
E-Modul von Brettschicht-Holz (BSH) E = 12000 N/mm2 = 12GPa
Schneehöhe von 62,5cm ergibt eine Schneelast von 125kg/m2
L = Belastung 1,25kN/m2 = 1250N/m2 = 125kg/m2 Schneelast + 20kg/m2 Ziegel & Holzlast
l = Spannweite 2,7m = 2700mm
a= Sparrenabstand 0,73m
q = Belastung L * a = 125kg/m2 * 0,73 = 91,25kg/m = 0,912kN/m
sigma b zul. = zulässige Spannung 10N/mm2 10MN/m2 100kg/cm2
max. Durchbiegung L/300 bei Nadelholz 1/300 = 3,33 mm/m
max. Durchbiegung L/200 bei BSH 1/200 = 5,00 mm/m
bei BSH Brettschichtholz sind allerdings max. 1/200 erlaubt)
w = max. zulässige Durchbiegung bei Nadelholz l / 300 = 2700mm / 300 = 9,0 mm
w = max. zulässige Durchbiegung bei BSH I / 200 = 2700mm / 200 = 13,5 mm
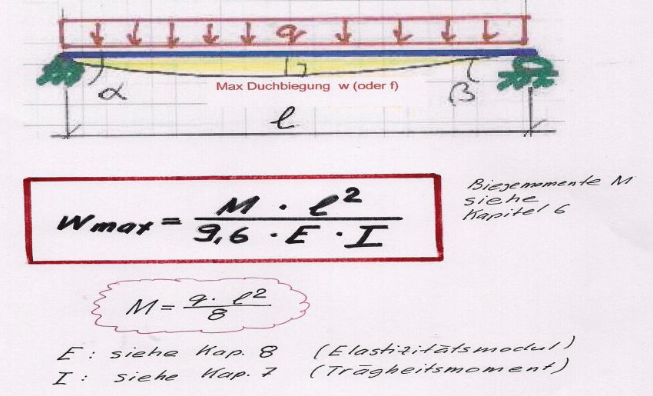
f = tatsächliche Durchbiegung = (M + l^2) / (9,6 * E * I)
Sparren
A = b * h = 4 * 12 cm = 48 cm2
Wx = (b * h^2) / 6 = (4 *12^2) / 6 = 96 cm3
Jx = (b * h^3) / 12 = (4 *12^3) / 12 = 576 cm4 ( = 5,76*10^6mm4 )
Pfetten 6x12 cm Fichte Leimbinder GL24 (BS11) SI nach DIN 1052
A = b * h = 6 * 12 cm = 72 cm2
Wx = (b * h^2) / 6 = (6 *12^2) / 6 = 144 cm3
Jx = (b * h^3) / 12 = (6 *12^3) / 12 = 864 cm4 (= 8,64*10^6 mm^4)
A = b * h = 4cm * 12cm = 48 cm2
Wx = (b * h^2) / 6 = (4 *12^2) / 6 = 96 cm3
Jx = (b * h^3) / 12 = (4 *12^3) / 12 = 576 cm4
M = (q * l^2) / 8 = (0,912kN/m * 2,7^2) / 8 = 0,831kN
f = (M + l^2) / (9,6 * E * I) = (0,831kN * 2700mm^2) / (9,6 * 10000N/mm2 * 5,76cm4) = 10,94mm (berechnete Durchbiegung)
********************************************************I*
Terrassendach Bräuwiese 15C
ÖNORM B4000 TL3 Windlasten
ÖNORM B4000 TL4 Schnee und Eislasten ALT
ÖNORM B4013 Schnee und Eislasten NEU Ausgabe 1983
Buchberg am Attersee Zone B Seehöhe 500m 1,75kN/m2 = 1750 N/m2 = 175 kg/m2
Schneehöhe von 62,5cm ergibt eine Schneelast von 125kg/m2
Fichte / Tanne
Spez. Gewicht = 0,3 .. 0,47 .. 0,7 kg/dm3 470 kg/m2
Zugfestigkeit = 4 .. 9,5 .. 24 kg/mm2 95 N/mm2
Druckfestigkeit = 3 .. 4,5 .. 7 kg/mm2 45 N/mm2
Biegefestigkeit = 4 .. 8 .. 12 kg/mm2 80 N/mm2
Schubfestigkeit = 0,3 .. 0,4 kg/mm2 4 N/mm2
https://wissenwiki.de/Vollholz
https://diglib.tugraz.at/download.php?id=576a769ebe73a&location=browse
Sparren Güteklasse II sigma zul. = 100kg/cm2
E-Modul von Holz E = 100000 kg/cm2 = 1000000 N/cm2 = 10000 N/mm2 = 10GPa = 1,45 Mpsi
https://de.wikipedia.org/wiki/Elastizitätsmodul
3,5m Sparren aus BSH 8x14cm
l = 350 cm = 3500 mm
Dachfläche = Neigung x Breite = 3,5m * 2,5m = 8,75 m2
Dachlast Fges = 8,75m2 * 1,75kN/m2 = 15,3kN
F = Fges / 2 = 15,3kN / 2 = 7,65kN = 765kg
A = b * h = 8 * 14 cm = 112 cm2
Wx = (b * h^2) / 6 = (8 *14^2) / 6 = 261cm3
Jx = (b * h^3) / 12 = (8 *14^3) / 12 = 1829cm4 (= 18,29*10^6 mm^4)
Mmax = Wx * sigma zul.= 261cm3 * 100kg/cm2 = 26133kpcm
Mmax = F * l / 8
F = Mmax * 8 / l = 26133kpcm * 8 / 350cm = 597kg
Wx = (F* l) / (8 * sigma zul.)
F = (Wx * 8 * sigma zul.) / l = (261cm3 * 8 * 100kg/cm2) / 350cm = 596,5kg
f = (5 * F * l^3) / (384 * E * Jx) = (5 * 596,5kg * 350cm^3) / (384 * 100.000kg/cm2 * 1829cm4) = 1,82cm = 18,2mm (berechnete Durchbiegung)
w = max. zulässige Durchbiegung bei Nadelholz l / 300 = 3500mm / 300 = 11,66 mm
w = max. zulässige Durchbiegung bei BSH I / 200 = 3500mm / 200 = 17,5 mm
********************************************************I*
Eingabedaten
Länge l = 3500 mm
Flächenträgheitsmoment Jx = 1829 cm4
Widerstandsmoment gegen Biegung Wx = 261 cm3
Elastizitätsmodul E = 10 GPa ( =10000 N/mm2 )
Streckenlast q = 1750 N/m
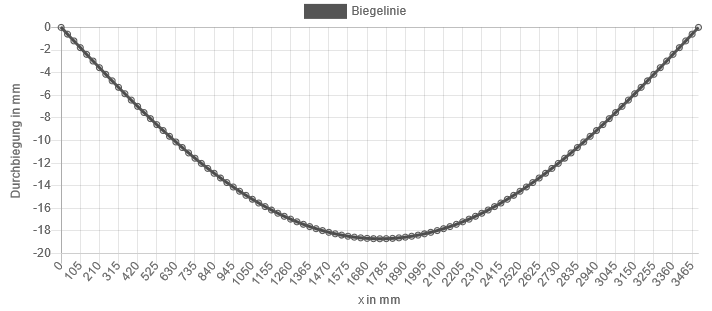
Ergebnisse
Durchbiegung fmax = 18,70 mm
Ort der Durchbiegung (l / 2) xfmax = 1750 mm
Winkel an Lager A αA = 0,98 °
Winkel an Lager B αB = 0,98 °
Maximales Biegemoment Mbmax = 2679,69 Nm
Maximale Biegespannung σbmax = 10,27 N/mm2
Lagerreaktion Fa = 3062,50 N
Lagerreaktion Fb = 3062,50 N
Quelle:
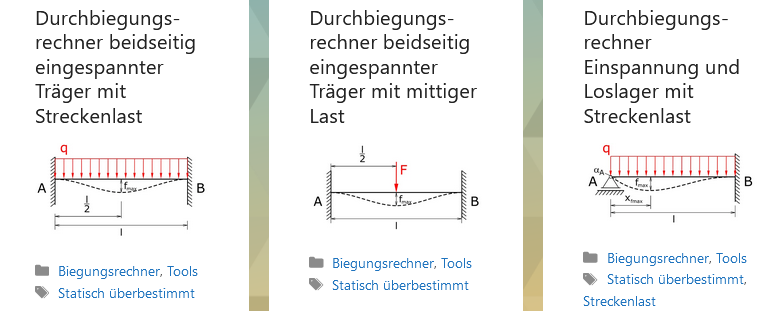
https://pickedshares.com/category/tools/durchbiegung-online-berechnen/
https://pickedshares.com/durchbiegungsrechner-gleichmasige-streckenlast/
********************************************************I*
Durchbiegung von Balken
Quelle:
https://de.wikipedia.org/wiki/Durchbiegung
Durchbiegungsrechner gleichmäßige Streckenlast
Brettschichtholz 6x12cm
Holzqualität nach DIN1052 TL1 BS-Holz GL28 = BS14 = GK1 oder Nadelholz S10
Feuchteklasse 18%
Sparren Güteklasse II sigma zul. = 1015kg/cm2
E-Modul von Holz E = 100000 kg/cm2 = 1000000 N/cm2 = 10000 N/mm2 = 10GPa = 1,45 Mpsi
E-Modul von Brettschicht-Holz (BSH) E = 12000 N/mm2 = 12GPa
Buchberg am Attersee Zone B Seehöhe 500m
L = Belastung 2,50kN/m2 = 2500N/m2 = 250kg/m2 Schneelast
l = Spannweite 3,5m = 350cm = 3500mm
a= Sparrenabstand 1,0m
q = Belastung L * a = 250kg/m2 * 3,5m = 875kg
z.B.: Belastung (Eigengewicht, Schnee, Wind,...): 2500 N/m2 2,5kN/m2
Sparrenabstand: 1,0 m
Belastung in kg/m = 2500N/m2 x 1,0 = 250 kg/m = 2500N/m = 2,5N/mm
sigma b zul. = zulässige Spannung 10N/mm2 10MN/m2 115kg/cm2
max. Durchbiegung L/300 bei Nadelholz 1/300 = 3,33 mm/m
max. Durchbiegung L/200 bei BSH 1/200 = 5,00 mm/m
bei BSH Brettschichtholz sind allerdings max. 1/200 erlaubt)
w = max. zulässige Durchbiegung bei Nadelholz l / 300 = 3500mm / 300 = 11,66 mm
w = max. zulässige Durchbiegung bei BSH I / 200 = 3500mm / 200 = 17,5 mm
f = tatsächliche Durchbiegung = (M + l^2) / (9,6 * E * I)
Sparren 6x12 cm Fichte Leimbinder GL24 (BS11) SI nach DIN 1052
A = b * h = 6 * 12 cm = 72 cm2 (Fläche) 7200 mm2
Widerstandsmoment Wx = (b * h^2) / 6 = (6 *12^2) / 6 = 144 cm3 144.000 mm3
Trägheitsmoment Jx = (b * h^3) / 12 = (6 *12^3) / 12 = 864 cm4 8.640.000 mm4 ( = 8,64*10^6 mm4 )
Mmax = Wx * sigma b zul. = 144cm3 * 115kg/cm2 = 16560kgcm
Biegemoment Mmax = (F * l) / 8
F = (Mmax * 8) / l = (16560 * 8) / 350 = 378,5kg
ODER
q = F = (8 * sigma b zul. * Wx ) / l = (8 * 115kg/cm2 * 144cm3) / 350 = 378,5kg
sigma b zul. = Mmax / Wx = 16560kgcm / 144cm3 = 115kg/cm2
Durchbiegung fmax = ( 5 * F * l^3) / 384 * E * Jx = (5 * 378,5 * 350cm^3) / (384 * 100000kg/cm * 864cm4) = 2,44cm
Durchbiegung fmax = 5 / 384 * (q * l^3) / ( E * Jx) = 5/384 * (378,5kg * 350^3) / (100000 * 864) = 2,44cm
********************************************************I*
BERECHNUNG VON DURCHBIEGUNGEN
Achtung:
Bei allen Berechnungen auf richtige Einheiten und Zahlengrössen achten!
E-Modul von Holz E = 100000 kg/cm2 = 1000000 N/cm2 = 10000 N/mm2 = 10GPa = 1,45 Mpsi
Widerstandsmoment Wx = (b * h^2) / 6 = (6 *12^2) / 6 = 144 cm3 144.000 mm3
Trägheitsmoment Jx = (b * h^3) / 12 = (6 *12^3) / 12 = 864 cm4 8.640.000 mm4
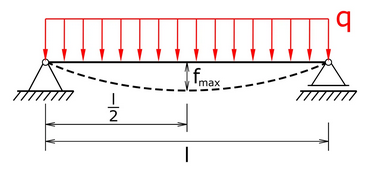
Berechnung der max. Durchbiegung beim einfachen Balken mit Streckenlast.
3m Sparren
Beispiel:
Einfacher Sparren aus Bauholz C24
E-Modul von Holz E = 100000 kg/cm2 = 1000000 N/cm2 = 10000 N/mm2 = 10GPa = 1,45 Mpsi
3m Sparren 6x12 cm Fichte
l = 3000 mm
Schneelast 250kg/m2 x 3m F = 750kg / 3m = 0,25kg/mm
A = b * h = 6 * 12 cm = 72 cm2 (Fläche)
Widerstandsmoment Wx = (b * h^2) / 6 = (6 *12^2) / 6 = 144 cm3 144.000 mm3
Trägheitsmoment Jx = (b * h^3) / 12 = (6 *12^3) / 12 = 864 cm4 8.640.000 mm4 ( = 8,64*10^6 mm4 )
Belastung in kg/m = 2500N/m2 x 1m Breite = 250 kg/m = 2500N/m = 2,5N/mm q = 2,5kN/m
Streckenlast q = 2,5 N/mm = 2,5kN/m
Md = (q * l^2) / 8 = (2,5kN/m * 3m^2) / 8 = 2,812 kNm = 2,812 * 10^6 Nmm
Wd = (Md * l^2) / (9,6 * E * Jx) = (2,812*10^6Nmm * 3000mm^2) / ( 9,6 * 10000 N/mm2 * 8,64*10^6 mm4 ) = 30,5mm
wd = max. zulässige Durchbiegung bei Holz l / 300 = 3000 mm / 300 = 10 mm (Faustformel)
Daher für 250kg Schnelast nicht geeignet
NEU
Belastung in kg/m = 1250N/m2 x 1m Breite = 1250 kg/m = 1250N/m = 1,25N/mm = 1,25kN/m
Md = (q * l^2) / 8 = (1,25kN/m * 3m^2) / 8 = 1,406 kNm = 1,406 * 10^6 Nmm
Wd = (Md * l^2) / (9,6 * E * Jx) = (1,406*10^6Nmm * 3000mm^2) / ( 9,6 * 10000 N/mm2 * 8,64*10^6 mm4 ) = 15,25mm
Wd = max. zulässige Durchbiegung bei Brettschicht-Holz l / 200 = 3000 mm / 200 = 15 mm (Faustformel)
Daher für 125kg Schnelast mit Leimholzbinder geeignet
Quelle:
http://goepf.bettschen.org/Statik9.pdf
********************************************************I*
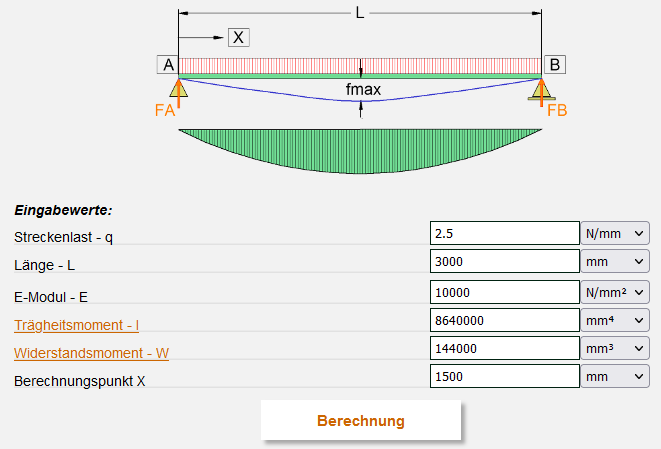
Biegeträger
Träger frei aufliegend mit Streckenlast
Schneelast 250kg/m2 x 3m F = 750kg / 3m = 0,25kg/mm
Streckenlast q = 2,5 N/mm
Länge L = 300mm
E-Modul E = 10000 N/mm
Trägheitsmoment 60x120mm Jx = 8640000 mm4
Widerstandsmoment 60x120mm Wx = 144000 mm3
FA = 3750N = 375kg
FB = 3750N = 375kg
max. Biegemoment bei 1,5m M = 2 812 500 Nmm
max. Biegespannung bei 1,5m sigma b = 19,5N/mm2
max. Durchbiegung bei 1,5m fmax = 30,5mm
Quelle:
https://www.schweizer-fn.de/festigkeit/biegung_traeger/biegung_traeger_start.php
https://www.schweizer-fn.de/festigkeit/biegung_traeger/frei_aufliegend/aufl2_sl_rech.php
********************************************************I*
Träger berechnen online
3m Sparren 6x12 cm Fichte 6/12
l = 3000 mm
Belastung in kg/m = 2500N/m2 x 1m Breite = 250 kg/m = 2500N/m = 2,5N/mm q = 2,5kN/m
Streckenlast q = 2,5 N/mm = 2,5kN/m
E-Modul von Holz E = 100000 kg/cm2 = 1000000 N/cm2 = 10000 N/mm2 = 10GPa = 1,45 Mpsi
A = b * h = 6 * 12 cm = 72 cm2 (Fläche)
Widerstandsmoment Wx = (b * h^2) / 6 = (6 *12^2) / 6 = 144 cm3 144.000 mm3
Trägheitsmoment Jx = (b * h^3) / 12 = (6 *12^3) / 12 = 864 cm4 8.640.000 mm4 ( = 8,64*10^6 mm4 )
Sparren aus Kantholz
KVH Konstruktionsvollholz
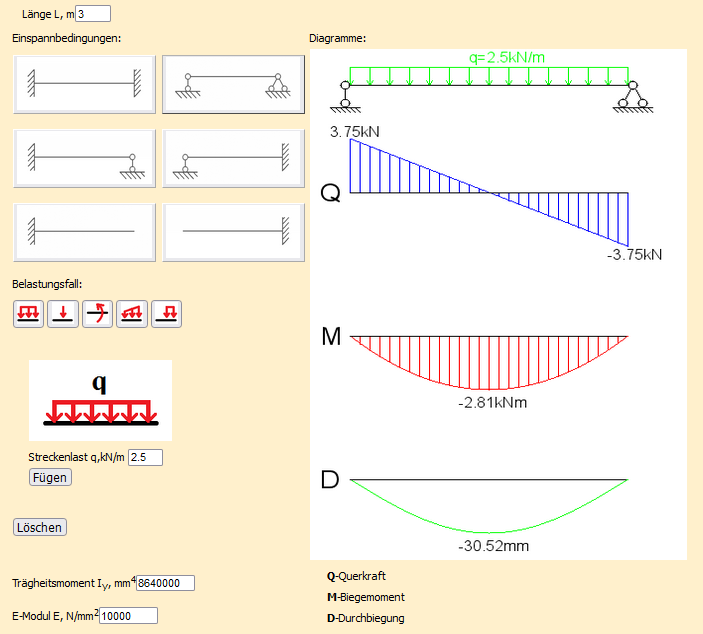
Gleichlast
Ergebnis:
Querkraft Q = 3,75 kN
Biegemoment Mmax = 2,81 kNm
Durchbiegung f = 30,52 mm
Berechnete max. Durchbiegung 30,25mm
wd = max. zulässige Durchbiegung bei Holz l / 300 = 3000 mm / 300 = 10 mm (Faustformel)
Daher für 250kg Schnelast nicht geeignet
Wd = max. zulässige Durchbiegung bei Brettschicht-Holz l / 200 = 3000 mm / 200 = 15 mm (Faustformel)
Daher für 125kg Schnelast mit Leimholzbinder geeignet
Beispiel:
Fichte 6/12 Sparren aus Kantholz - KVH Konstruktionsvollholz
l = 3 m = 3000 mm
Kraft (Punktlast) F = 6 kN = 600 kg
E-Modul von Holz E = 100000 kg/cm2 = 1000000 N/cm2 = 10000 N/mm2 = 10GPa = 1,45 Mpsi
A = b * h = 6 * 12 cm = 72 cm2 (Fläche)
Widerstandsmoment Wx = (b * h^2) / 6 = (6 *12^2) / 6 = 144 cm3 144.000 mm3
Trägheitsmoment Jx = (b * h^3) / 12 = (6 *12^3) / 12 = 864 cm4 8.640.000 mm4 ( = 8,64*10^6 mm4 )
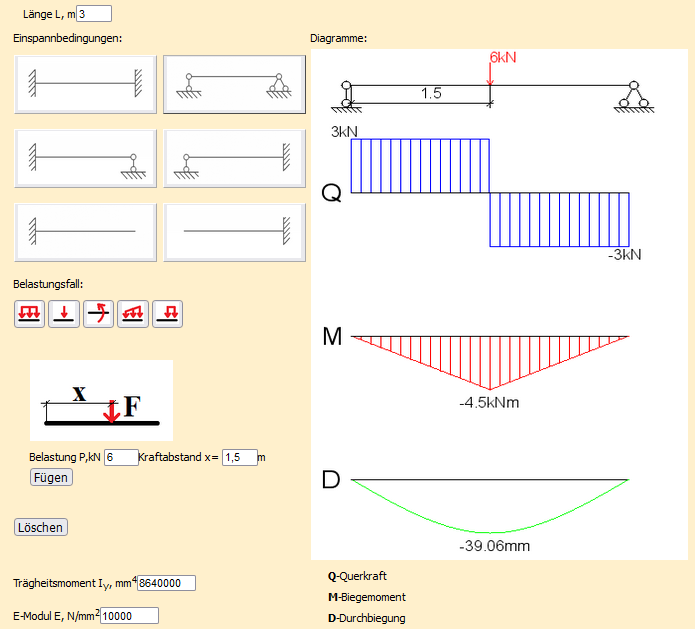
Punktlast
Ergebnis:
Querkraft Q = 3,0 kN
Biegemoment Mmax = 4,5 kNm
Durchbiegung f = 39,06 mm
Quelle:
http://rascheta.net/beamde/
********************************************************I*
Träger auf zwei Stützen Jahresabo kostet € 95,- ! ! !
braucht keiner - alle Formeln auf meinen Seiten schon zu finden!
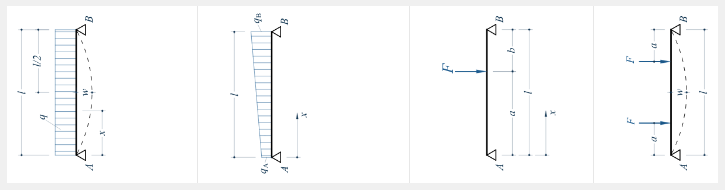
Konstante Streckenlast Trapezförmige Streckenlast Einzellast 2 Einzellasten
Konstante Streckenlast
Berechnung von Auflagerkräften, Biegemomenten und Durchbiegung bei einem Trager auf zwei Stützen mit konstanter Streckenlast
Konstante Streckenlast
Der Elastizitätsmodul (Formelzeichen E mit der Einheit N/mm²) beschreibt den Zusammenhang zwischen Spannung und Dehnung bei der Belastung von festen Stoffen.
Je geringer die Verformung eines Materials beim Auftreten einer Spannung ist, desto höher ist sein Elastizitätsmodul.
Die nachfolgende Tabelle zeigt die E-Module einiger Werkstoffe.
Werkstoff E in N/mm²
Baustahl St37 210.000
Gußeisen 169.000
Aluminium 70.000
Stahl
180.000 bis 220.000 N/mm2
Kupfer 130.000
Magnesium 44.000
Glas 50.000 bis 80.000
Holz (längs zur Faser) 10.000 N/mm² bis 15.000 N/mm²
Holz
(quer zur Faser) 300 bis 1000 (Hirnholz)
Stahlbeton 27.000 bis 45.000
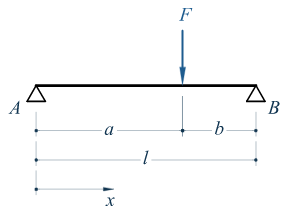
Träger auf zwei Stützen - Einzellast
Berechnung von Auflagerkräften, Biegemoment und Durchbiegung bei einem Träger auf zwei Stützen mit einer Einzelast
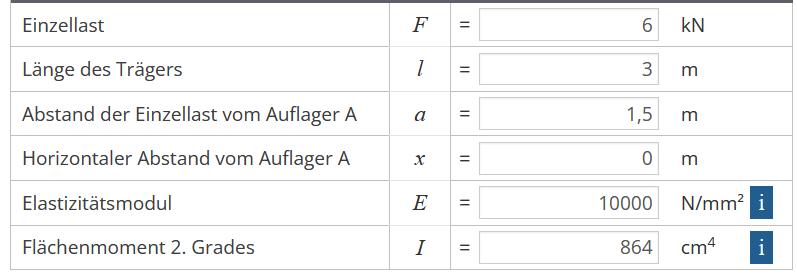
F = 6 kN = 6.000n = 600kg
l = 3 m
a = 1,5 m
x = 0 m
E = 10.000 N/mm
Sparren 6/12
Trägheitsmoment 60x120mm Jx = 864cm^4 = 8.640.000 mm4
Widerstandsmoment 60x120mm Wx = 144 cm3 = 144.000 mm3
Quelle:
https://www.bauformeln.de/statik/traeger-auf-zwei-stuetzen/konstante-streckenlast/
https://www.bauformeln.de/statik/traeger-auf-zwei-stuetzen/
********************************************************I*
Berechnung eines Holzträgers
Streckenlast
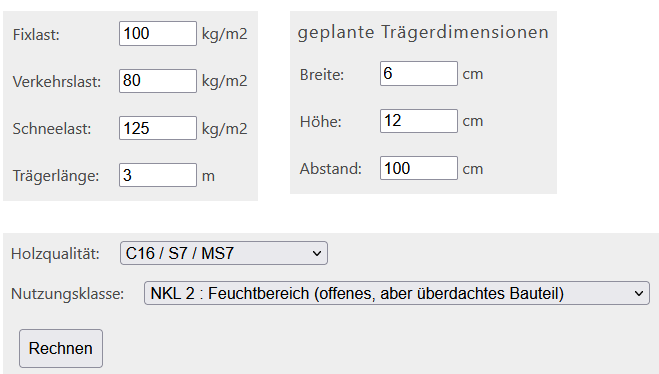
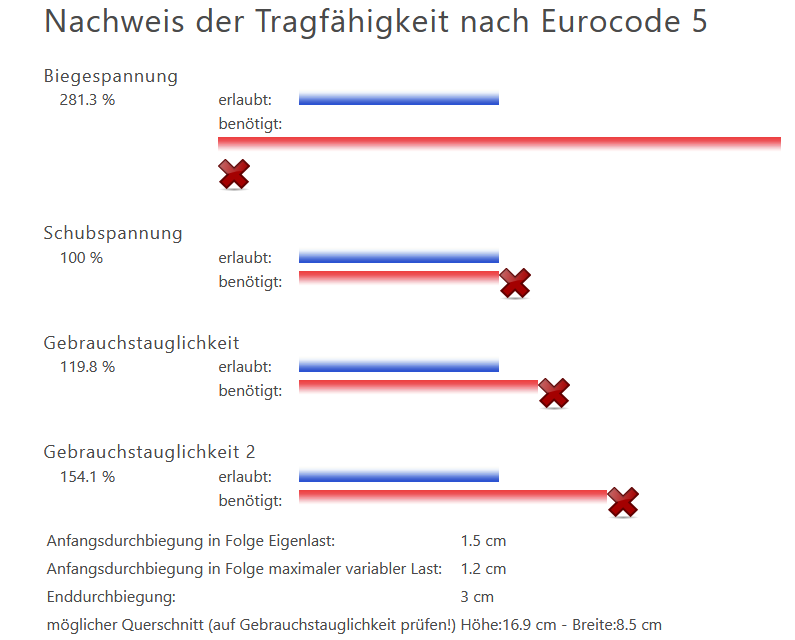
Berechnung einzelner Holzträger oder Balken. Die Berechnung erfolgt gemäß Eurcode 5, der europaweit gültigen Norm zur statischen Berechnung von Holzkonstruktionen.
Bedingung:
Träger mit Streckenlast - die Last muss über die gesamte Länge relativ gleich verteilt wirken, nicht als einzelne punktuelle Last.
Der Träger liegt horizontal.
Schneelastberechnung stimmt nicht über 2000m Seehöhe.
Schneelast 125..250 kg/m2
Fixlast: 20 kg
Verkehrslast: 80 kg
Schneelast 430kg
Trägerlänge 3m
Brettschichtholz Breite 6cm Höhe 12cm
Holzqualität nach DIN1052 TL1 BS-Holz GL28 = BS14 = GKI
Nutzungsklasse NKL 2: Feuchtbereich (offenes, aber überdachtes Bauteil)
egal ob man 0 kg Schneelast eingibt oder 500kg Schneelast die Biegewerte ändern sich nicht!
http://www.eurocode-statik-online.de/einzeltraeger.php
Quelle:
https://www.eurocode-statik-online.de/flaeche.php
http://www.eurocode-statik-online.de/
********************************************************I*
Statik berechnen für Heimwerker
Berechnung einer Holzbalkenfläche
Quelle:
http://www.eurocode-statik-online.de/flaeche.php
http://www.eurocode-statik-online.de/
********************************************************I*
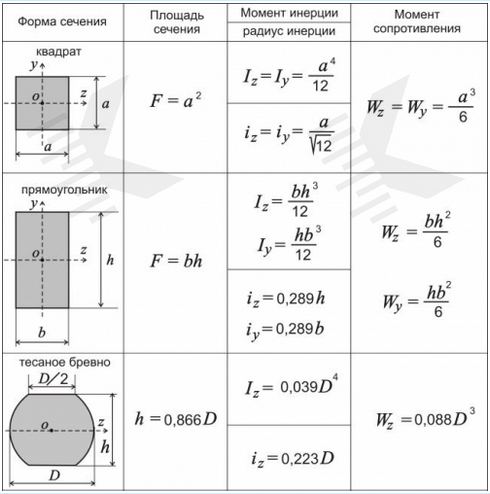
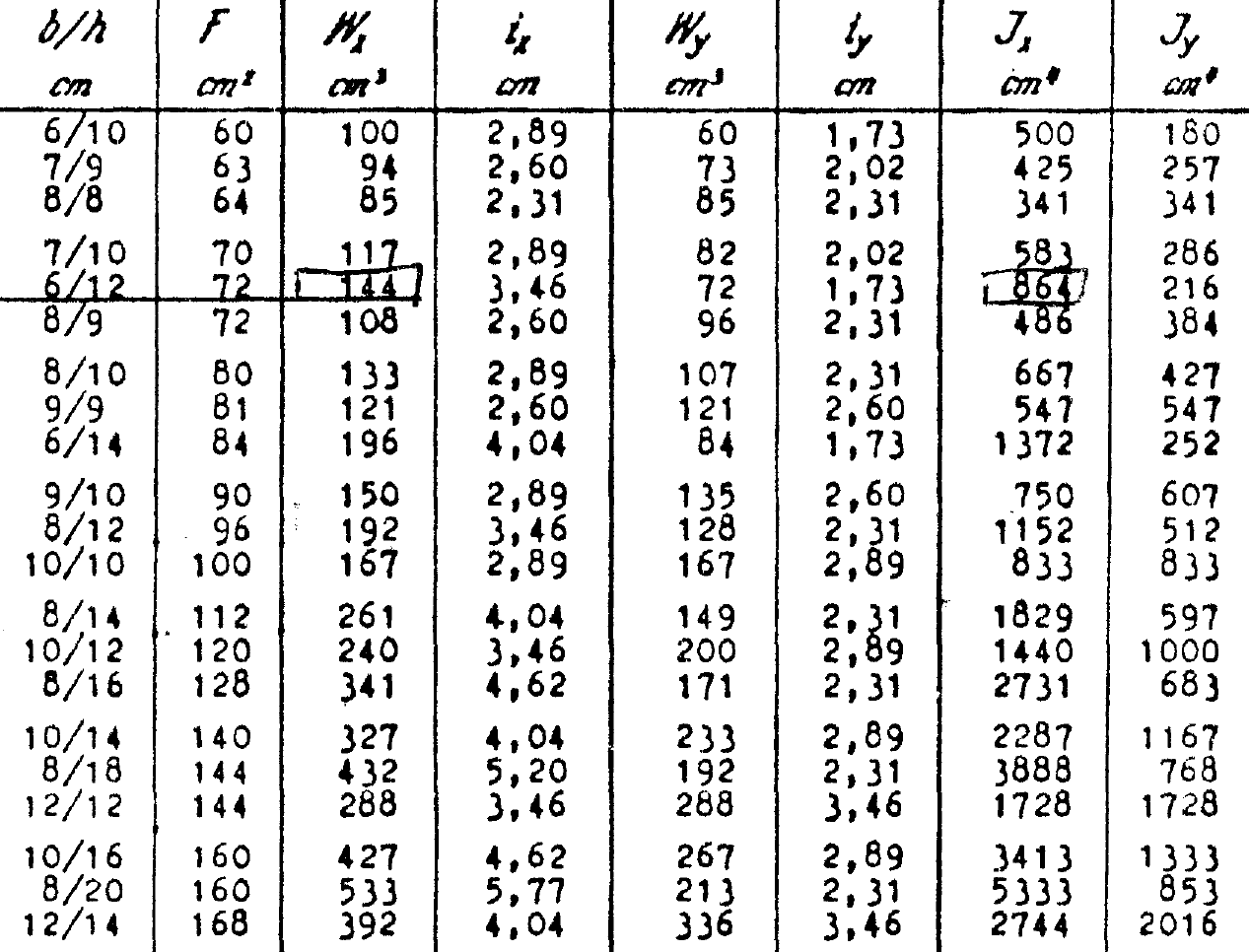
Balken und Kanthölzer aus Nadelholz - Querschnittsmaße und statische Werte
Christiani Datenbank D Werkstoffe Seite D 62
A = l * b = 8 * 14 = 112cm2
Wx = (b * h^2) / 6 = (8 *14^2) / 6 = 261cm3
Jx = (b * h^3) / 12 = (8 *14^3) / 12 = 1.829cm4 (= 18,29*10^6 mm^4)
Querschnitte Widerstandsmomente Trägheitsmomente
b/h in cm A in cm2 Wx in cm3 Wy in cm3 Jx in cm4 Jy in cm4
6/6 36 36 36 108 108
6/8 48 64 48 256 144
6/10 60 100 60 500 180
6/12 72 144 72 864 216
6/14 84 196 84 1 372 252
6/16 96 256 96 2 044 288
6/18 103 324 108 2 916 324
6/20 120 400 120 4 000 360
8/8 64 85 85 341 341
8/10 80 133 107 667 427
8/12 96 192 128 1152 512
8/14 112cm2 261cm3 149cm3 1829cm4 597cm4
8/16 128 341 171 2731 683
8/18 144 432 192 3888 768
8/20 160 533 213 5333 853
10/10 100 167 167 833 833
10/12 120 240 200 1440 1 000
10/14 140 327 233 2287 1 167
10/16 160 427 267 3413 1 333
10/18 180 540 300 4860 1 500
10/20 200 667 333 6667 1 667
10/22 220 807 367 8873 1 833
10/24 240 960 400 11520 2 000
10/26 260 1127 433 14647 2 167
12/12 144 288 288 1728 1 728
12/14 168 392 336 2744 2 016
12/16 192 512 384 4096 2 304
12/18 216 648 432 5832 2 592
12/20 240 800 480 8000 2 880
12/22 264 968 528 10648 3 168
12/24 288 1152 576 13824 3 456
12/26 312 1352 624 17576 3 744
14/14 196 457 457 3201 3 201
14/16 224 597 523 4779 3 659
14/18 252 756 588 6801 4 116
14/20 280 933 652 9333 4 573
14/22 308 1129 719 12422 5 031
14/24 336 1344 784 16128 5 488
14/26 364 1577 849 20505 5 945
300_b_fritz-x_Bemessungstabellen - Kanthölzer aus Nadelholz - Querschnittsmaße und statische Werte_1a.pdf
Holz - Kanthölzer
Holzabmessungen siehe ÖNORM B3001
Querschnitte und statische Werte
********************************************************I*
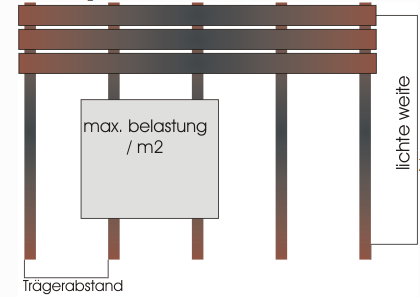
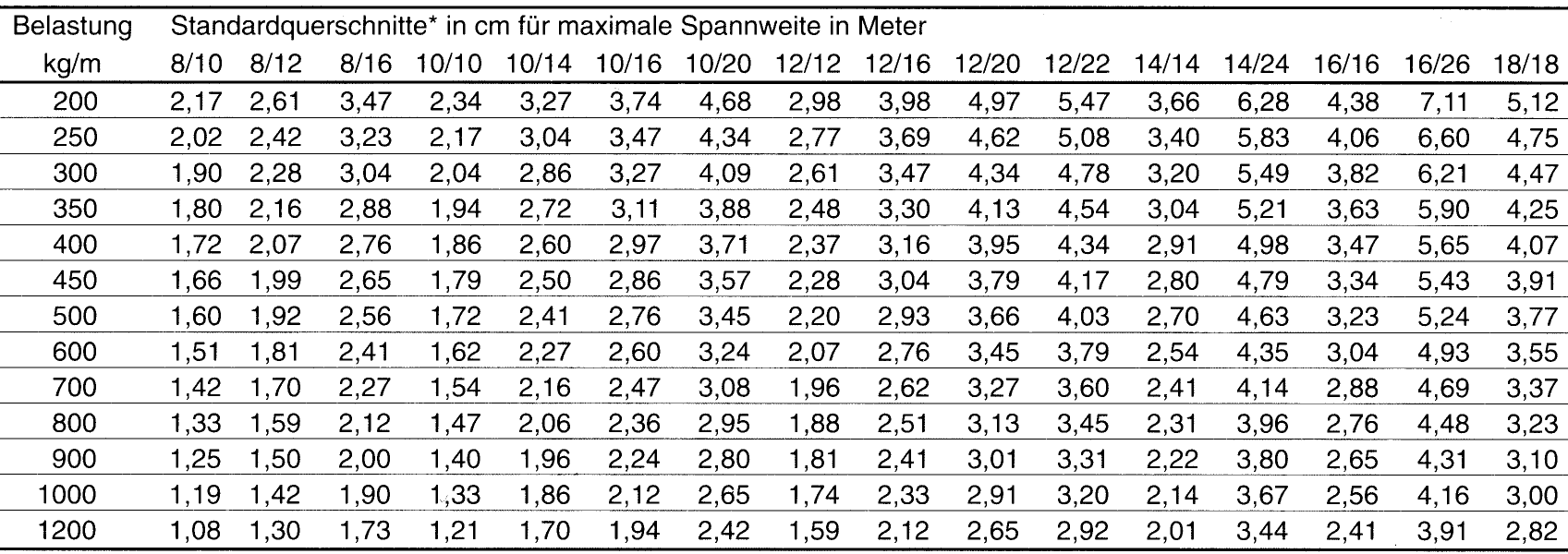
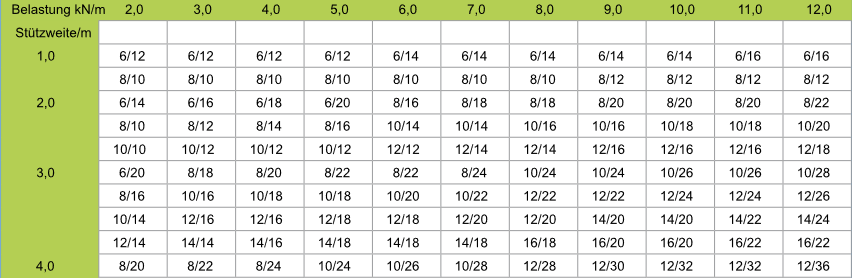
Belastung und Querschnitte
Diese Tabelle dient als Bemessungshilfe und ersetzt keine genaue statische Berechnung.
Je Querschnitt und Belastung ist die maximal mögliche Spannweite angegeben.
Bemessungsgrundlagen:
a) Elastitätsmodul: 12000 N/mm2
b) Zulässige Spannung: 13,2 N/mm2
c) Maximale Durchbiegung: L/300 bei Nadelholz 1/300 = 3,3 mm/m
(Bei Brettschichtholz sind allerdings 1/200 = 5,0 mm/m erlaubt)
z.B.: Belastung (Eigengewicht, Schnee, Wind,...): 410 kg/m2.
Binderabstand: 1,20 m
Spannweite: 5,2m.
Belastung in kg/m = 410 x 1,20 = 492 kg/m
Erforderlicher Querschnitt lt. Tabelle: 16/26
Die in der Tabelle angegebenen Stützweiten dienen für eine überschlägige vorbemessung von Brettschichtholz Sparren.
Festigkeitsklasse: GL 24h
Elastizitätsmodul: 11000 N/mm2
Maximale Durchbiegung: L/300
bei Nadelholz 1/300 = 3,3 mm/m
Bei Brettschichtholz sind allerdings 1/200 = 5,0 mm/m sogar erlaubt
https://www.dowaholz.de/pdfs/BSH-Bemessungshilfe.pdf
z.B.: Belastung (Eigengewicht, Schnee, Wind,...): 175kg/m2 = 1750N/m2 1,75kN/m2
Binderabstand: 1 m
Spannweite: 3,5m
Belastung in kg/m = 175kg/m2 x 1 = 175kg/m 1,75kN/m
Erforderlicher Querschnitt lt. Tabelle: 8/14
Quelle:
https://www.klh.at/wp-content/uploads/2019/07/klh-vorbemessungstabellen.pdf
********************************************************I*
Norm [ZURÜCKGEZOGEN]
DIN 1055-5:1975-06
Lastannahmen für Bauten; Verkehrslasten, Schneelast und Eislast € 39,90
Ausgabedatum 1975-06
Schneelast-NORM / Schneelastnormung
Schneehöhe von 87,5cm ergibt eine Schneelast von 175kg/m2
Schneehöhe von 62,5cm ergibt eine Schneelast von 125kg/m2
10 cm Schnee wiegen etwa 20 kg/m² (Schneewichte = 2,0 kN/m³)
10 cm Pulverschnee wiegen etwa 10 kg/m² (Schneewichte = 1,0 kN/m³)
10 cm Nassschnee wiegen bis zu 40 kg/m³ (Schneewichte = 4,0 kN/m³)
10 cm Eis wiegen bis zu 90 kg/m³ (Eiswichte = 9,0 kN/m³)
Quelle:
https://de.wikipedia.org/wiki/Schneelast
Korrekturfaktoren f für geneigte Dächer nach DIN1055 TL5
z.B.
Schneelast Sk = 1kN/m2 = 100 kg/m2 (auf die Waagrechte)
Dachneigung alpha = 35°
Korrekturfaktor laut Tabelle µ1 = 0,67
Tatsächliche Schnelast s =
s = µ1 * Sk = 100 kg/m2 * 0,67 = 67 kg/m2
300_b_fritz-x_DIN1055-5 Schneelasten und Eislasten Korrekturfaktoren f=1,23 für 35° geneigte Dächer_1a.pdf
********************************************************I*
DIN 1055-5 : Lastannahmen für Bauten; Verkehrslasten, Schneelasten und Eislasten
Wo ist die zulässige Schneelast geregelt?
Die Schneelast, die beim Standsicherheitsnachweis für ein Gebäude angesetzt wird, ist in der
Norm DIN 1055-5 „Lastannahmen für Bauten - Verkehrslast; Schneelast und Eislast"
geregelt.
Sie ist in der DIN-Norm in kN/m2 (Kilonewton pro Quadratmeter) angegeben.
Die Schneelast kann mit der DIN 1055-5 für jeden Standort eines Gebäudes in Abhängigkeit von der Schneelastzone und der Gebäudehöhe ermittelt werden.
Sie ist zugleich auch die zulässige Schneelast auf dem Dach eines Gebäudes, die nicht überschritten werden soll. Eine zulässige Schneelast von
z.B. 1 kN/m2 bedeutet, dass 100 kg Schnee auf 1 m2 Dachfläche zulässig sind.
Eine gewisse Überschreitung der Schneelast wird - ebenso wie die Alterung sowie geringfügige Abweichungen bei der Planung und Herstellung des Gebäudes - durch entsprechende Sicherheiten beim Standsicherheitsnachweis berücksichtigt.
BUCH:
DIN 1055-5, Juni 1975. Lastannahmen für Bauten; Verkehrslasten, Schneelast und Eislast.
1975, 5 S.
Beuth Verlag GmbH
300_b_fritz-x_DIN1055-5 Die alte DIN 1055 TL5 Lastannahmen für Bauten - Verkehrslasten Schneelast und Eislast_1a.pdf
300_b_fritz-x_DIN1055-5 Die neue DIN 1055 TL5 Schnee- und Eislasten_1a.pdf
********************************************************I*
BRETTSCHICHTHOLZ BSH BEMESSUNG
Einfeldträger
Maximale Spannweite (m)
Unter Einhaltung der zulässigen Biegespannungen und der Durchbiegungsbeschränkung L/300 sowie der maximalen Querkraft am Auflager
Quelle:
https://www.binderholz.com/fileadmin/user_upload/pdf/produkte/brettschichtholz.pdf
Bemessung von BS-Holz-Bauteilen nach EN 1995-1-1 (EC 5)
holzbauhandbuch | REIHE 2 | TEIL 1 | FOLGE 2
INFORMATIONSDIENST HOLZ
Quelle:
https://www.brettschichtholz.de/publish/binarydata/pdfs/aktuelles/idh_bemessung-von-bs-holz-bauteilen_print_160309.pdf
********************************************************I*
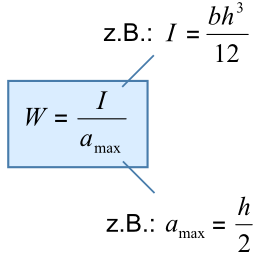
Biegewiderstandsmoment für einfache Querschnittformen berechnen
Biegung berechnen, Biegespannung berechnen
DMS Biegebalken
Grundlagen der Biegebelastung
Beanspruchung eines Bauteils auf Biegung
Festigkeitsberechnungen (4): Biegung
Festigkeitsberechnungen (5): Übungsaufgaben zu Biegung
Wie groß ist die Biegespannung?
Biegespannung σb = Mb : W
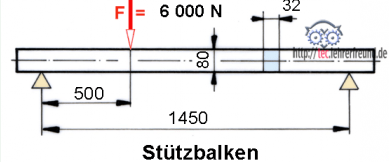
Mb= FA ∙ l
Hier muss man zuerst die linke Stützkraft FA berechnen. Der
Drehpunkt des Hebels wird ins rechte Lager gelegt.
Mrechts =
Mlinks
FA ∙ 1 450 = F ∙ 950
FA = 6 000 N ∙ 950 mm : 1 450 mm = 3 931 N
Mb= FA ∙ 50 cm = 3 931 N ∙ 50 cm
Mb = 196 552 Ncm
Widerstandsmoment W = b ∙ h2 : 6 = 3,2 cm ∙ (8 cm)2 : 6 =
W = 34,13 cm3
Biegespannung σb = Mb : W = 196 552 Ncm : 34,13 cm3 =
σb = 5 759 N/cm2 = 57,6 N/mm2
Quelle:
https://www.lehrerfreund.de/technik/1s/festigkeitsberechnungen-4-biegung/3701
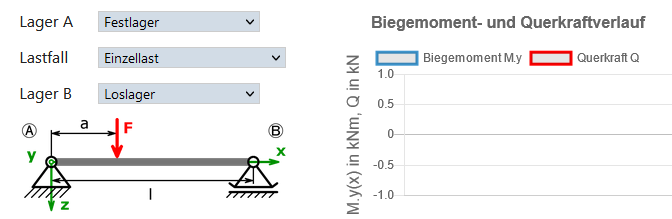
Rechner für Auflagerreaktionen, Querkraft & Biegemoment von statisch (un)bestimmt gelagerten Balken
Rechner für Auflagerreaktionen, Querkraft & Biegemoment von statisch (un)bestimmt gelagerten Balken
Erklärung der Abkürzungen
Fliegende L. ist die Abkürzung für fliegende Lagerung; die Kraft F greift außerhalb der beiden Lager an.
Fa = Auflagerkraft im Lager A in z-Richtung; in x-Richtung wirken keine Kräfte!
Fb = Auflagerkraft im Lager B in z-Richtung; in x-Richtung wirken keine Kräfte!
Ma = Einspannmoment im Lager A
Mb = Einspannmoment im Lager B; bei fliegender Lagerung Moment im Balken bei x = a.
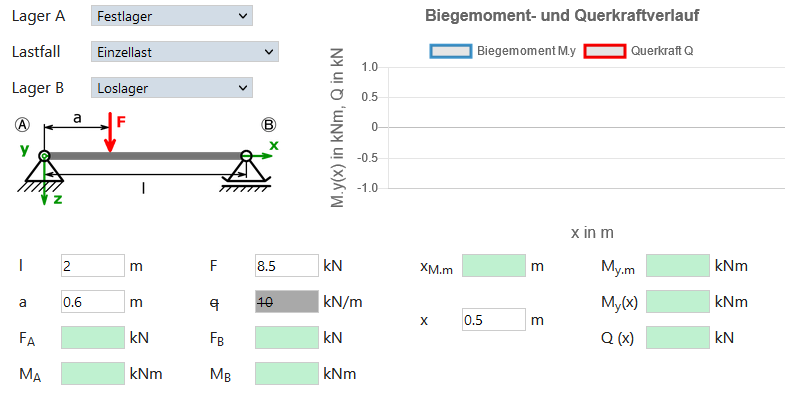
xM.m = Stelle des maximalen Biegemoments; Achtung: es wird auch bei mehreren, gleich großen Biegemomenten nur eine Stelle angegeben!
My.m = maximales Biegemoment
x = beliebige Stelle, an der das Biegemoment, die Querkraft, die Biegespannung und die Durchbiegung berechnet werden soll
My (x) = Biegemoment an der Stelle x
Q (x) = Querkraft an der Stelle x
A = Querschnitt des Profils
Wst. = Werkstoff („Material“)
E = E-Modul, passende Werte gibt es zum Beispiel auf
Wikipedia
Iy
= Flächenträgheitsmoment
Wy = Widerstandsmoment
σx = Biegespannung in der Randfaser an der Stelle x
σx.m = maximale Biegespannung im Balken an der Stelle xM.m. Es ist zu prüfen, ob der Balken diese
Spannung auch aushält!
αA = Neigungwinkel (= Verdrehung) des Balkens im Lager A
αB = Neigungwinkel (= Verdrehung) des Balkens im Lager B
xf.m = Stelle der maximalen Durchbiegung des Trägers
fmax = maximale Durchbiegung des Balkens an der Stelle xf.m unter der Last F. Es ist eventuell zu prüfen, ob diese Durchbiegung auch zulässig ist! In der Regel reicht es jedoch, wenn nur die Spannungen kontrolliert werden.
f (x) = Durchbiegung (= Verschiebung) des Balkens an der Stelle x
Quelle:
https://www.johannes-strommer.com/rechner/balkenberechnung/
https://www.johannes-strommer.com/formeln/auflagerreaktionen-durchbiegung-winkel/
Biegung berechnen, Biegespannung berechnen
Biegespannung berechnen - Formel
σb – Biegespannung
Mb – Biegemoment
W – Widerstandsmoment
F – Kraft (Querkraft)
x – Abstand (der Kraft F vom Festlager des Balkens)
σb = Mb / W =_______ N/m2
Mb = σb * W
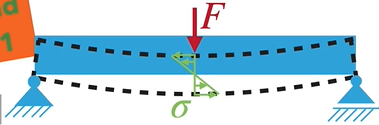
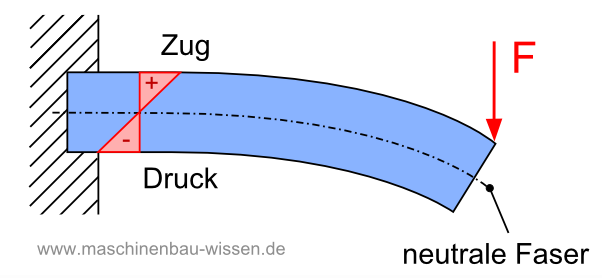
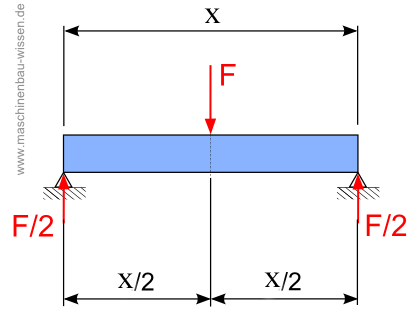
Träger ruht auf zwei Stützen
Auf den auf zwei Stützen ruhenden Träger wirkt mittig die Kraft F. Das Biegemoment ergibt sich, indem der Biegequerschnitt, wie im Bild dargestellt, von der Seite betrachtet wird.
Es lassen sich sowohl die Kraft F/2 als auch der Abstand x/2 erkennen.
Das Biegemoment berechnet sich nun wie folgt:
Mb = (F / 2) * (x / 2)
Mb = F * (x / 4)
Quelle:
https://www.maschinenbau-wissen.de/skript3/mechanik/balken-biegung/210-biegewiderstandsmoment1
Berechnungsprogramm:
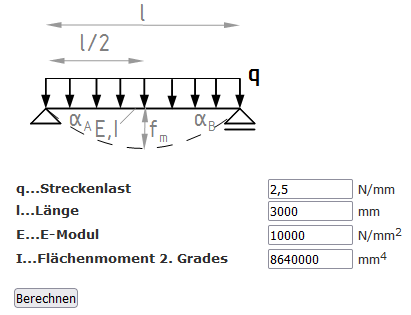
Gelagerter Balken mit Streckenlast
Mit diesem Programm kann die Durchbiegung f und der Neigungswinkel für einen zweiseitig gelagerten Balken, Träger oder Stab mit Streckenlast online berechnet werden.
Zur Berechnung der Balkenbiegung müssen die Streckenlast q, die Balkenlänge l, der E-Modul E und das Flächenmoment 2. Grades I (Flächenträgheitsmoment) eingegeben werden.
Schneelast F= 250kg/m2
Streckenlast q = 250kg/m2 = 0,25kg/mm = 2,5 N/mm
Sparrenlänge l = 3m = 3000 mm
E-Modul E = 10.000 N/mm
Sparren 6/12
Trägheitsmoment 60x120mm Jx = 864cm^4 = 8.640.000 mm4
Widerstandsmoment 60x120mm Wx = 144 cm3 = 144.000 mm3
fm = 30.518 mm max. Durchbiegung
αA = αB = 1.865 °
Quelle:
http://www.maschinenbau-fh.de/s_balken_gq.php
********************************************************I*
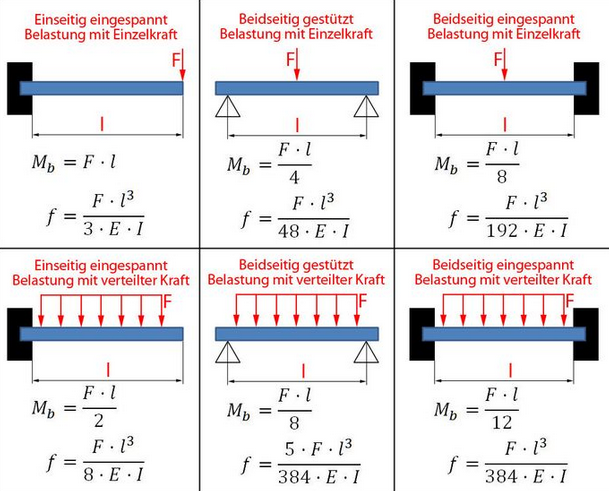
Biegemoment berechnen
Dadurch, dass das Biegemoment (Mb) von der Art der Krafteinwirkung und von der Lagerung der Enden abhängig ist, gibt es mehrere Formeln für die Berechnung, die nachfolgend abgebildet sind.
Die Formeln für die Durchbiegung (f) sind ebenfalls dargestellt.
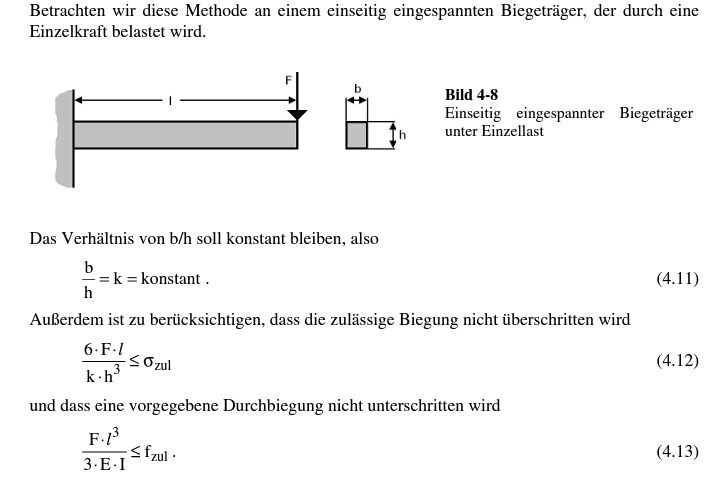
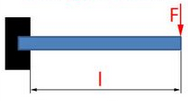
Beispiel für ein Bauteil, das einseitig eingespannt und mit Einzelkraft belastet ist:
Kraft (F): 5000 N
Stablänge (l): 300 cm
Elastizitätsmodul (E): 19600000 N/cm²
Flächenmoment des 2. Grades (I): 1360 cm4
Gesucht: Biegemoment Mb, Durchbiegung f
Berechnung für Biegemoment: 5000 · 300 = 1500000 Ncm = 15000 Nm
Berechnung für Durchbiegung: 5000 · 27000000 : (3 · 19600000 · 1360) = 1,688 cm
Biegespannung berechnen
Ist das Biegemoment ermittelt, kann man die Biegespannung berechnen.
Die Formel ist:
σb = Mb / W =
Beispiel:
Biegemoment (Mb): 1500000 Ncm
Widerstandsmoment (W): 151 cm³
Gesucht: Biegespannung σb
Berechnung: 1500000 : 151 = 9933,77 N/cm² = 99,3377 N/mm²
Beispiel für ruhende, statische Belastung (Belastungsfall I):
Biegegrenze (σbF): 330 N/mm²
Sicherheitszahl 3
Gesucht:
Zulässige Biegespannung σb zul
Berechnung:
330 : 3 = 110 N/mm²
Das zulässige Biegemoment und das erforderliche Widerstandsmoment berechnen
Mit Hilfe der zulässigen Biegespannung (σb zul) kann man das zulässige Biegemoment (Mb zul) oder das erforderliche Widerstandsmoment (Werf) berechnen.
Die Formeln hierfür sind:
Mb = σb * W
W = Mb / σb
Beispiel für das zulässige Biegemoment:
Zulässige Biegespannung (σb zul): 110 N/mm²
Widerstandsmoment (W): 151 cm³ = 151000 mm³
Gesucht:
Zulässiges Biegemoment Mb zul
Berechnung:
110 · 151000 = 16610000 Nmm = 16610 Nm
Beispiel für das erforderliche Widerstandsmoment:
Zulässige Biegespannung (σb zul): 110 N/mm²
Biegemoment (Mb): 1500 Nm = 1500000 Nmm
Gesucht:
Erforderliches Widerstandsmoment Werf
Berechnung:
1500000 : 110 = 13636,3636 mm³ = 13,6363 cm³
Quelle:
https://www.cnc-lehrgang.de/biegebeanspruchung/
DIN A4 ausdrucken
********************************************************I*
Impressum: Fritz Prenninger, Haidestr. 11A, A-4600 Wels, Ober-Österreich, mailto:
[email protected]
ENDE













%20Stati-4d709be4f408f969.png)